Class 12 Mathematics Sample Paper Set I
Please see below Class 12 Mathematics Sample Paper Set I with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.
CBSE Sample Paper for Class 12 Mathematics Set I
SECTION – A
1. If

= A , then write the order of matrix A.
Solution: Note that

= A so, order of matrix A is 1×1.
2.

Solution:

⇒ x(-x2 -1) -sin θ(-x sin θ – cosθ) + cosθ(-sin θ + x cosθ) = 8
⇒ -x3 – x + x sin2 θ + sin θcos θ – cos θsin θ + x cos2 θ = 8 = ⇒- x3 – x + x(sin2 θ + cos2 θ) = 8
⇒ -x3 = 8 ∴ x = -2 .
3. If

is written as A = P + Q , where P is a symmetric matrix and Q is skew symmetric matrix, then write the matrix P.
Solution:

4. If a̅, b̅ and c̅ are unit vectors such that a̅ + b̅ + c̅ = o̅ , then write the value of a̅.b̅ + b̅.c̅ + c̅.a̅ .
Solution: As a̅ + b̅ + c̅ = o̅ ⇒ (a̅ + b̅ + c̅).(a̅ + b̅ + c̅) = o̅.o̅
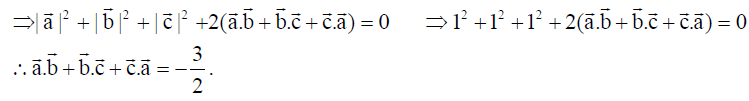
5. If |a̅ x b̅|2 + |a̅.b̅|2 = 400 and |a̅| = 5 , then write the value of |b̅| .
Solution:
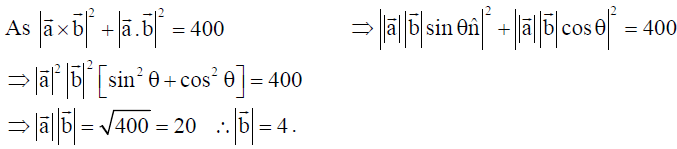
6. Write the equation of a plane which is at a distance of 5√3 units from origin and the normal to which is equally inclined to coordinate axes.
Solution: Since the normal to the required plane is equally inclined to the coordinate axes so, its d.c.’s are
1/√3 , 1/√3 , 1/√3 .
So, the equation of plane is, x/√3 + y/√3 + z/√3 = 5√3 or , x + y + z =15 .
SECTION – B
7. Prove that : cot-1 √1+sin x + √1-sin x/√1+sin x – √1-sinx = x/2 , 0 < x < π/2 .
Solution:

OR
Solve for x : tan-1(x-2/x-1) + tan-1(x+2/x+1) = π/4 .
Solution:

8. A coaching institute of English (subject) conducts classes in two batches I and II and fees for rich and poor children are different. In batch I, it has 20 poor and 5 rich children and total monthly collection is ₹ 9000, whereas in batch II, it has 5 poor and 25 rich children and total monthly collection is ₹ 26,000. Using matrix method, find monthly fees paid by each child of two types. What values the coaching institute is inculcating in the society?
Solution: Let each poor child pay ₹ x per month and each rich child pay ₹ y per month.
Clearly, 20x + 5y = 9000…(i) and 5x + 25y = 26000…(ii)
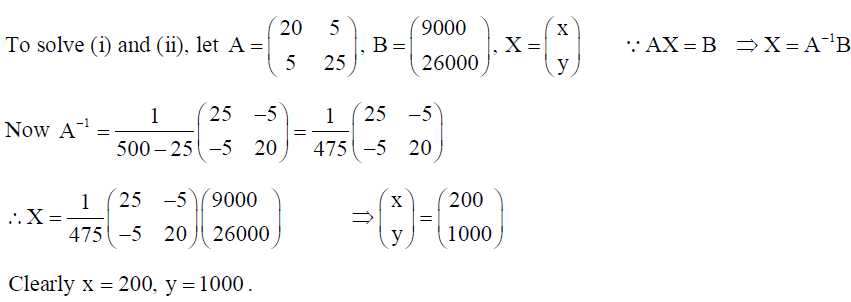
Hence each poor child pays ₹ 200 per month and each rich child pays ₹ 1000 per month.
Value reflected : Helpfulness towards the needy and poor students.
9. Find the values of a and b, if the function f defined by f(x) =

is differentiable at x =1.
Solution: Since f (x) is differentiable at x =1 so it’s continuous at x =1 as well.
Continuity at x =1 :

10. Differentiate tan-1(1+x2 -1/x) w.r.t. sin-1 2x/1+x2 , if x ∈ (-1,1) .
Solution: Let u = tan-1(1+x2-1/tanθ) Put x = tan θ ⇒ θ = tan-1 x
⇒ = tan-1(√1+tan2θ – 1/tanθ) = tan-1(secθ -1/tanθ) = tan-1(1-cosθ/sinθ)
⇒ = tan-1(tan θ/2) = θ/2 ⇒ 2u = tan-1 x…(i)
Also let v = sin-1 2x/1+x2 = 2tan-1 x ⇒ v = 2 x 2u [By (i)
On diff. w.r.t. v both sides, d/dv (v) = 4 x d/dv (u) ⇒ du/dv = 1/4 .
OR
If x = sin t and y = sin pt , prove that (1+x2) d2y/dx2 – x dy/dx + p2y = 0 .
Solution: Here x = sin t and y = sin pt ⇒ dx/dt ⇒ dx/dt = cos t and dy/dt = p cos pt
∴ dy/dx = dy/dt x dt/dx = p cos pt/cos t ⇒ cos t dy/dx = p cos pt
Diff. w.r.t. x both sides, cos t d2y/dx2 – dy/dx sin t x dt/dx = -p2 sin pt x dt/dx
⇒ cos t d2y/dx2 – x dy/dx x 1/cos t = -p2y x 1/cos t ⇒ cos2 t d2y/dx2 – x dy/dx = -p2y
⇒ (1-sin2 t) d2y/dx2 – x dy/dx + p2y = 0 ∴ (1-x2) d2y/dx2 – x dy/dx + p2y = 0 .
11. Find the angle of intersection of the curves y2 = 4ax and x2 = 4by .
Solution: We have y2 = 4ax and x2 = 4by
Solving these equations we get the point of intersections as : P(0,0) & Q(4a1/3b2/3 , 4a2/3b1/3 ) .
Now y2 = 4ax ⇒ 2y dy/dx = 4a ⇒ dy/dx = 2a/y and x2 = 4by ⇒ 2x = 4b dy/dx ⇒ dy/dx = x/2b

Hence the angle of intersection at P and Q are respectively : π/2 , tan-1(3a1/3b1/3/2(a2/3 + b2/3) .
12. Evaluate :

Solution:

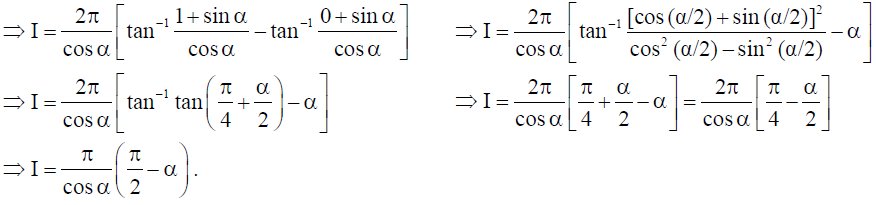
13. Find :
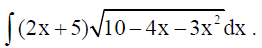
Solution:

OR
Find :

Solution:

14. Find :

Solution:


15. Solve the differential equation : y2dx + (x2 – xy + y2 )dy = 0 .
Solution: Here y2dx + (x2 – xy + y2 )dy = 0 ⇒ dx/dy = xy – x2 – y2/y2 = x/y -(x/y)2 -1

16. Solve the differential equation : (cot-1 y + x)dy = (1+ y2 )dx .
Solution: Here (cot-1 y + x)dy = (1+ y2 )dx ⇒ dx/dy + x(-1/1+y2) = cot-1y/1+y2
It is in the form of dy/dx + P(y) x = Q(y) where P(y) = -1/1+y2 and Q(y) cot-1y/1+y2

17. If a̅ x b̅ = c̅ and a̅ x c̅ = b̅ x d̅ , show that a̅ – b̅ is parallel to b̅ – c̅ , where a̅ ≠ b̅ and b̅ ≠ c̅ .
Solution: Given a̅ x b̅ = c̅ x d̅ and , a̅ x c̅ = b̅ x d̅ ….(i)

18. Prove that the line through A(0, –1, –1) and B(4, 5, 1) intersects the line through C(3, 9, 4) and D(–4, 4, 4).
Solution:

Hence the lines are in the same plane so, they must intersect each other.
19. A box has 20 pens of which 2 are defective. Calculate the probability that out of 5 pens drawn one by one with replacement, at most 2 are defective.
Solution: Let the selection of defective pen be considered success so, p = 2/20 = 1/10 , q = 9/10 . Here n is 5.
Using Binomial distribution, P(X = r) = nCr qn-r , we get :
P(r ≤ 2) = P(r = 0) + P(r =1) + P(r = 2)

OR
Let X denote the number of colleges where you will apply after your results and P(X = x) denotes your probability of getting admission in x number of colleges. It is given that

where k is a positive constant. Find the value of k. Also find the probability that you will get admission in (i) exactly one college (ii) at most 2 colleges (iii) at least 2 colleges.
Solution:

⇒ k x 0 + k x 1 + 2k x 2 + 5k – k x 3 + 5k – k x 4 = 1 ⇒ 8k =1 ∴ k = 1/8 .
(i) P(x = 1) k x 1 = 1/8
(ii) P(x ≤ 2) = P(x = 0) + P(x = 1) + P(x = 2) = k x 0 + k x 1 + 2k x 2 = 5k = 5/8
(iii) P(x ≥ 2) = 1 – P(x < 2) =1 – {P(x = 0) + P(x = 1)}= 1 – k x 0 + k x 1} = 1 – k = 1 – 1/8 = 7/8 .
SECTION – C
20. If f ,g :R → R be two functions defined as f (x) = |x| + x and g(x) = |x| – x , ∀ x ∈ R . Then
find fog and gof. Hence find fog(-3) , fog(5) and gof (-2) .
Solution: Here f (x) = |x| + x and g(x) = |x| – x , ∀ x ∈ R

21. If a, b and c are all non-zero and
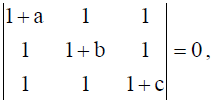
then prove that 1/a + 1/b + 1/c + 1 = 0
Solution:


OR
If

find adj.A and verify that 3 A(adj.A) = (adj.A)A = |A| I3 .
Solution:

22. The sum of the surface areas of a cuboid with sides x, 2x and x/3 and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of sphere. Also find the minimum value of the sum of their volumes.
Solution: Let r be the radius of the sphere.
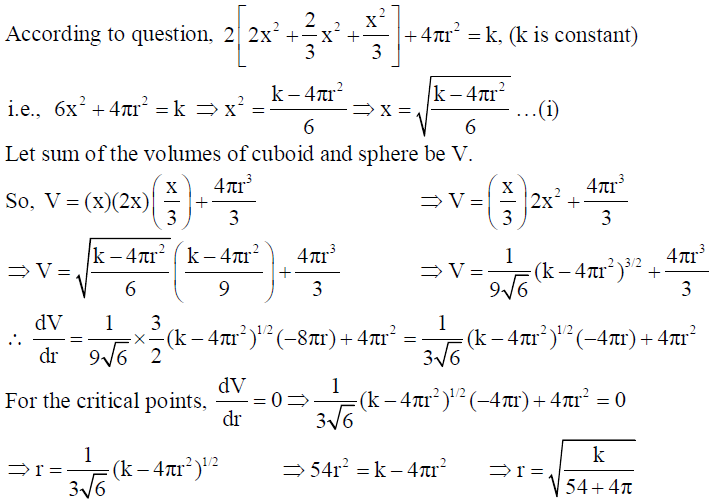

OR
Find the equation of tangents to the curve y = cos(x + y), – 2π ≤ x ≤ 2π that are parallel to the line x + 2y = 0 .
Solution: We’ve y = cos(x + y), x ∈ [-2π, 2π]

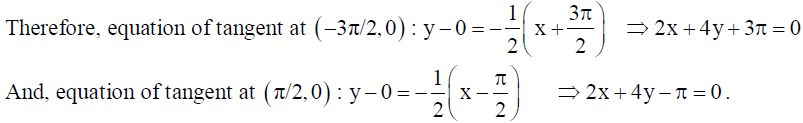
23. Using integration find the area of the region bounded by the curves y = √4 – x2 , x2 + y2 – 4x = 0 and the x-axis.
Solution: Given circles are y = √4 – x2 …(i) and, x2 + y2 – 4x = 0…(ii)

24. Find the equation of the plane which contains the line of intersection of the planes x + 2y + 3z – 4 = 0 and 2x + y – z + 5 = 0 and whose x-intercept is twice its z-intercept.
Hence write the vector equation of a plane passing through the point (2, 3, –1) and parallel to the plane obtained above.
Solution: Equation of the family of planes passing through two given planes is,
(x + 2y + 3z – 4) + k(2x + y – z + 5) = 0
⇒ (1+ 2k)x + (2 + k)y + (3- k)z = 4 – 5k…(i) 24
When k = 1/5 , plane (i) becomes 7x + 11y + 14z = 15 …(A)
When k = 4/5 , plane (ii) becomes 13x + 14y + 11z = 0 …(B)
Note that (B) has to be rejected as it does not satisfy the given conditions.
Now equation of plane through (2, 3, –1) and parallel to plane (A) is,
7(x – 2) +11(y -3) + 14(z +1) = 0 i.e., 7x + 11y + 14z + 33 ∴ r̅ .(7î + 11ĵ + 14k̂) = 33
25. Bag A contains 3 red and 5 black balls, while bag B contains 4 red and 4 black balls. Two balls are transferred at random from bag A to bag B and then a ball is drawn from bag B at random.
If the ball drawn from bag B is found to be red, find the probability that two red balls were transferred from A to B.
Solution: Let E : ball drawn from bag B is red, H1 : 2 red balls are transferred, H2 : 1 red and 1 black ball are transferred and H3 : 2 black balls are transferred.
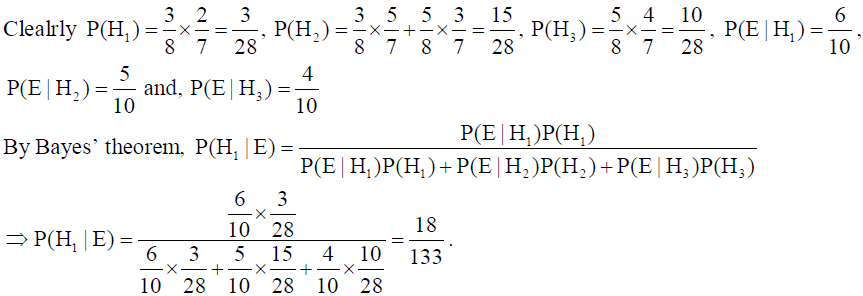
26. In order to supplement daily diet, a person wishes to take X and Y tablets. The contents (in milligrams per tablet) of iron, calcium and vitamins in X and Y are given as below :

The person needs to supplement at least 18 milligrams of iron, 21 milligrams of calcium and 16 milligrams of vitamins. The price of each tablet of X and Y is ₹ 2 and ₹ 1 respectively. How many tablets of each type should the person take in order to satisfy the above requirement at the minimum cost? Make an LPP and solve graphically.
Solution: Let number of tablets of type X and type Y be x and y respectively.
To minimize : Z = 2x + y in ₹
Subject to constraints : x ≥ 0, y ≥ 0 ,
6x + 2y ≥ 18 ⇒ 3x + y ≥ 9,
3x + 3y ≥ 21 ⇒ x + y ≥ 7,
2x + 4y ≥ 16 ⇒ x + 2y ≥ 8


As the feasible region is unbounded so,
Z = 8 may or may not be minimum value.
To check, draw 2x + y < 8 .
As 2x + y < 8 has no point in common with the feasible region.
So, Z < ₹ 8 is the minimum value of Z.
And, the number of tablets of type X and type Y are 1 and 6 respectively.
