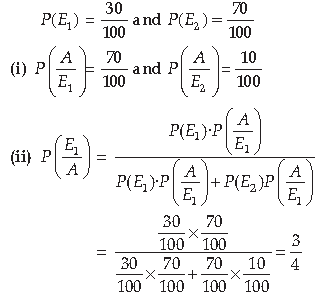Please see below Class 12 Mathematics Sample Paper Term 2 Set B with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Term 2 Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.

CBSE Sample Paper for Class 12 Mathematics Term 2 Set B

Section A

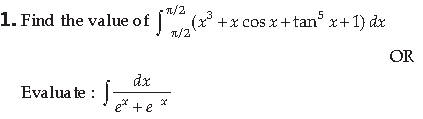
Answer.

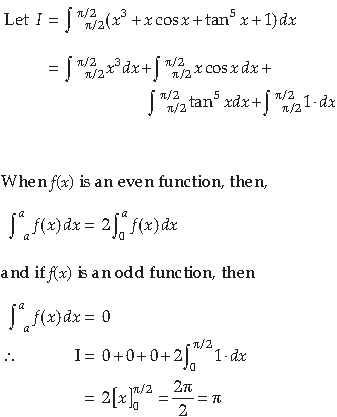
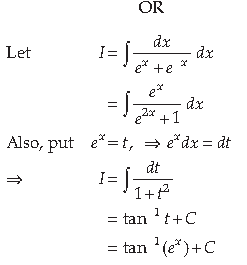
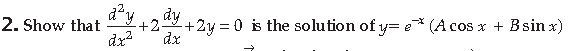
Answer. Given that, y = e^–x (A cos x + B sin x)
On differentiating both sides w.r.t., x we get

Answer.

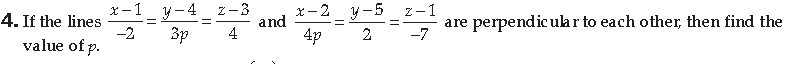
Answer. Using formula for perpendicular condition,
l₁l₂ + m₁m₂ + n₁n₂ = 0
or – 8p + 6p – 28 = 0
or – 2p = 28
∴ p = – 14

5. If P(A) = 0.4, P(B) = 0.8 and P (B/A) = 0.6, then P(A ∪ B)
Answer. Here,
P (A) = 0.4, P(B) = 0.8 and P (B/A) = 0.6

6. Find the probability distribution of X, the number of heads is a simultaneous toss of two coins.
Answer. Let X be the number of heads.
Possible values of X are 0, 1, 2.

Section – B

Answer. Let

8. Find the general solution of (dy/dx) + y tan x = sec x

                                          OR
Solve the differential equation:

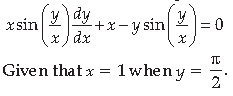
Answer. Given differential equation is

Above differential equation is a homogeneous equation
Put y = vx

9. If a̅ = î + 2j + 3k and b̅ = 2î + 4j + 5k represent two adjacent sides of a parallelogram, find unit vectors parallel to the diagonals of the parallelogram.
Answer. Given that, a̅ = î + 2j + 3k and b̅ = 2î + 4j + 5k are two adjacent sides of a parallelogram.
Let us suppose d̅₁ and d̅₂ are two diagonals of parallelogram.

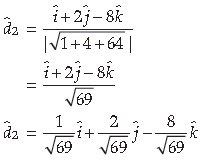
10. Find the shortest distance between the lines:
r̅ = (t + 1) î + (2 – t) ĵ + (1 + t) k̂
r̅ = (2a + 2) î – (1 – s) ĵ + (2s – 1) k̂
                                                                                       OR
A plane meets the co-ordinate axes at A, B and C such that the centroid of DABC is the point (a, b, g). Show that the equation of the plane is

Answer. Equations of lines can be written as :

Since, the equation of the plane having intercept a, b and c on the three co-ordinate axes is:

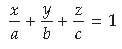
Here, the co-ordinates of A, B and C are (a, 0, 0), (0, b, 0) and (0, 0, c) respectively.

Section – C

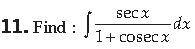
Answer.

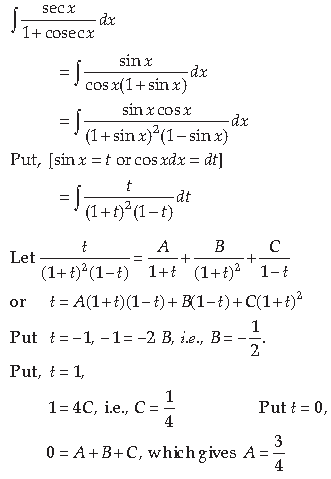
12. Find the area bounded by lines x = 2y+ 3, y – 1 = 0 and y + 1 = 0.
                                                          OR
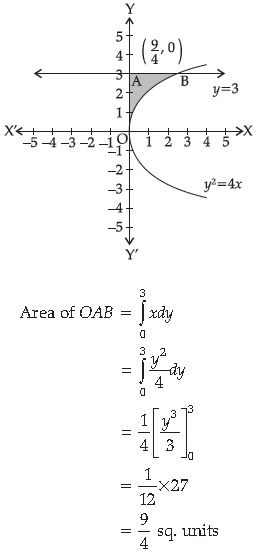
Find the region bounded by the curve y² =4x, y-axis and the line y = 3.
Answer.

The area bounded by the curve, y² = 4x,
y-axis, and y = 3 is represented as :

13. Find the equation of plane passing through the points A(3, 2, 1), B(4, 2, –2) and C(6, 5, –1) and hence
find the value of λ for which A(3, 2, 1), B(4, 2, –2), C(6, 5, –1) and D(λ, 5, 5) are coplanar.
Answer. A plane which passes through A(3, 2, 1), B(4, 2, –2) and C(6, 5, –1) is

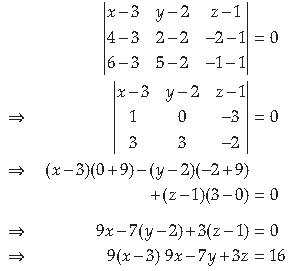
Thus, plane passing through point A, B and C is 9x – 7y + 3z = 16
Now, given A, B, C and D (l, 5, 5) are coplanar.
So, D lies on the plane passing through A, B and C
∴ 9λ – 7(5) + (5) = 16
⇒ 9λ = 36
⇒ λ = 4

Case-Based/Data Based

14. Of the students in a school, it is known that 30% have 100% attendance and 70% students are irregular. Previous year results report that 70% of all students who have 100% attendance attain A grade and 10% irregular students attain A grade in their annual examination. At the end of the year, one student is chosen at random from the school and he was found to have an A grade. Let E₁ and E₂ be the events that selecting a student with 100% attendance and selecting a student who is not regular, respectively.

Based on the above information, answer the following questions

(i) Find the values of P (A/E₁) and P (A/E₂)
(ii) What is the probability that the student has 100% attendance
Answer. Let E₁ : Selecting a student with 100% attendance
E₂ : Selecting a student who is not regular
A : selected student attains A grade.