Class 11 Mathematics Sample Paper
Refer to below provided Class 11 Mathematics Sample Paper with solutions. These Guess papers for Mathematics Class 11 have been designed based on the latest examination guidelines and paper pattern issued by CBSE. We have provided all Sample Papers for Class 11 Mathematics with answers. You can click on the links below to access the practice papers for free.
CBSE Sample Papers for Class 11 Mathematics
Class 11 Mathematics Paper Term 2 Set A
PART – A
Section – I
1. The value of cos (35° + A) cos (35° – B) + sin (35° + A) sin (35° – B) is equal to
(a) sin (A + B)
(b) sin (A – B)
(c) cos (A + B)
(d) cos (A – B)
Answer
C
2. If a parallelopiped is formed by planes drawn through the points (2, 3, 5) and (5, 9, 7) parallel to the coordinate planes, then find the length of the diagonal.
(a) 7 units
(b) 5 units
(c) 8 units
(d) 3 units
Answer
A
3. Consider the experiment of rolling a die. Let A be the event of ‘getting a prime number and B be the event of ‘getting an odd number’, then A but not B =
(a) {1}
(b) {1, 2}
(c) {2}
(d) {3, 5}
Answer
C
4. If f(x) = x + 1/x , then find f ′ (x).
(a) 1+1/x2
(b) 1+1/x
(c) 1 – x2
(d) 1- 1/x2
Answer
D
Section – II
Case study-based question is compulsory. Attempt any 4 sub parts. Each sub-part carries 1 mark.
5. Nishtha and Naira are sisters and were playing with two dice. They decided to threw both the dice simultaneously and note down the sum of numbers which come up on two dice.

Based on the above information, answer the following question.
(i) The probability that the sum is even,
(a) 1/2
(b) 1/3
(c) 1/4
(d) 1/6
Answer
A
(ii) The probability that the sum is multiple of 3.
(a) 12/13
(b) 1/4
(c) 5/6
(d) 1/3
Answer
D
(iii) The probability that the sum is less than 4.
(a) 12/13
(b) 11/12
(c) 1/12
(d) 3/13
Answer
C
(iv) The probability if that sum is greater than 11.
(a) 1/36
(b) 1/12
(c) 1/16
(d) 1/18
Answer
A
(v) The probability if the sum is not less than 4.
(a) 7/9
(b) 11/12
(c) 5/9
(d) 4/9
Answer
B
PART – B
Section – III
6. If tan x = 3 cot x, if x lies in 1st quadrant, then find the value of sin x.
Answer: We have, tan x = 3 cot x ⇒ tan2x = 3
⇒ tan x = √3 ∴ sin x = √3/2
7. Find the value of sin(40° + q) cos(10° + q) – cos(40° + q) sin(10° + q).
Answer: We have,
sin(40° + q)⋅cos(10° + q) – cos(40° + q)⋅sin(10° + q)
= sin{(40° + q) – (10° + q)} = sin30° = 1/2
8. How many different signals can be made by 5 flags from 8 flags of different colours?
Answer:The number of ways of arranging 5 flags out of 8 flags = 8P5 = 8!/(8-5)! = 8!/3! = 8.7.6.5.4.3!/3! = 6720
OR
If 1/8! + 1/9! = x/10! , then find x.
Answer: Given, 1/8! + 1/9! = x/10! ⇒ 10!/8! + 10!/9! = x
⇒ 10 × 9 + 10 = x ⇒ x = 100
9. What is the eccentricity of the hyperbola 3×2 – 4y2 = – 12?
Answer: The given equation can be written as
-x2/4 + y2/3 = 1
The eccentricity of this hyperbola is given by
e = √1+a2/b2 = √1+ 4/3 = √7/3
10. In a town of 6000 people, 1200 are over 50 years old and 2000 are females. It is known that 30% of the females are over 50 years. What is the probability that a randomly chosen individual from the town is either female or over 50 years?
Answer: Let E1 = event of person being a female,
and E2 = event of person being 50 years old.
Then, n(E1) = 2000, n(E2) = 1200,
and n(E1 ∩ E2) = (30% of 2000) = 600.
Now, n(E1 ∪ E2) = n(E1) + n(E2) – n(E1 ∩ E2) = 2600.
∴ P(E1 ∪ E2) = 2600/6000 = 13/30 .
Section – IV
11. If 3x-4/2 ≥ x+1/4 – 1, then find the internal in which x lies.
Answer: We have 3x-4/2 ≥ x+1/4 – 1
or 3x-4/2 ≥ x-3/4 or 2(3x – 4) ≥ (x – 3)
or 6x – 8 ≥ x – 3 or 5x ≥ 5 or x ≥ 1
Thus all real numbers which are greater than or equal to 1 is the solution set of the given inequality.
∴ x ∈ [1, ∞)
OR
If cot x = 3/4 and x lies in third quadrant, then find the value of sec x.
Answer: Since, sec2x = 1 + tan2 x = 1 +(3/4)2 = 25/16
On taking square root, we get sec x = ± 5/4
But x lies in third quadrant, so sec x = – 5/4
12. Prove : cos (π/4+x) +cos (π/4- x) = √2 cosx .
Answer:
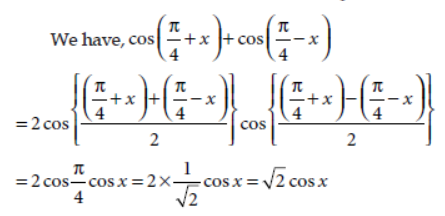
13. Find the equation of the curve formed by the set of all points whose distance from the points (3, 4, –5) and (–2, 1, 4) are equal.
Answer: Let P(x, y, z) be any point on the given curve, and
A(3, 4, –5) and B(–2, 1, 4) be the given points. Then, PA
= PB ⇒ PA2 = PB2
⇒ (x –3)2 + (y – 4)2 + (z + 5)2 = (x + 2)2
+ (y – 1)2 + (z – 4)2
⇒ 10x + 6y – 18z – 29 = 0.
14. Find the derivative of 1/ax2 + b , with respect to x.
Answer: Let y = 1/ax2+b
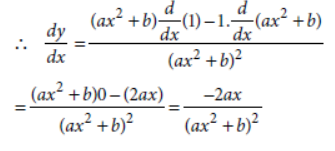
Section -V
15. If sin4 θ/a + cos4 θ/b = 1/a+b , then prove that sin12 θ/a5 + cos12 θ/b5 = 1/(a+b)5 .
Answer: Given, sin4 θ/a + cos4 θ/b = 1/a+b
⇒ (sin2 θ)2/a + (1-sin2 θ)2/b = 1/a+b
⇒ λ2b(a + b) + (a + b) a (1 – l)2 = ab, where l = sin2q
⇒ λ2ab + l2b2 + a2 + a2l2 – 2a2l + ab + abl2 – 2abl = ab
⇒ λ2a2 + l2b2 + 2abl2 + a2 – 2a2l – 2abl = 0
⇒ λ2{a2 + b2 + 2ab} + a2 – 2la (a + b) = 0
⇒ {λ(a + b)}2 + a2 – 2la (a + b) = 0
⇒ {λ(a + b) – a}2 = 0
⇒ l = a/a+b ⇒ sin2θ = a/a+b …(i)
From (i), cos2q = 1 – sin2q = 1 – a/a+b = b/a+b …(ii)
Using (i) and (ii), we get
sin12 θ/a5 + cos12 θ/b5 = (sin2 θ)6/a5 + (cos2 θ)6/b5
= (a/a+b)6/a5 + (b/a+b)6/b5
= a/(a+b)6 + b(a+b)6 = a+b/(a+b)6 = 1/(a+b)5 .
16. A manufacturer has 600 litres of a 12% solution of acid. How many litres of a 30% acid solution must be added to it so that acid content in the resulting mixture will be more than 15% but less than 18%?
Answer: Let x litres of 30% acid solution is required to be
added. Then
Total mixture = (x + 600)litres
∴ 30% of x + 12% of 600 > 15% of (x + 600)
and 30% of x + 12% of 600 < 18% of (x + 600)
or 30x/100 + 12/100 (600) > 15/100 (x +600)
and 30x/100 + 12/100 (600) > 18/100 (x +600)
or 30x + 7200 > 15x + 9000 and 30x + 7200 < 18x + 10800
or 15x > 1800 and 12x < 3600 or x > 120 and x < 300.
i.e., 120 < x < 300
Thus, the number of litres of the 30% solution of acid will have to be more than 120 litres but less than 300 litres.
OR
Find the solution of l1/x – 2l < 4 .
Answer:
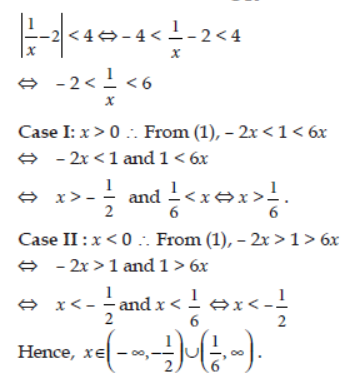
17. If f(x) = sin x + cos x, then find f ′ (x) using first principle.
Answer:
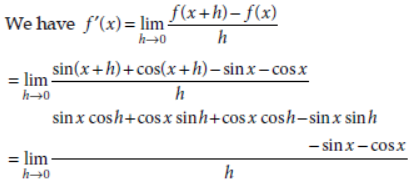
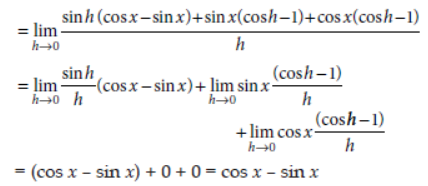
Section -VI
18. Find the number of ways in which four letters from the word MATHEMATICS can be arranged.
Answer: Available letters are MMAATTHEICS
There are 11 letters in which 2 M’s, 2 A’s and 2 T’s.
The following cases are possible :
Case I : When four letters consist of two pair of similar
letters. We can choose such letters in 3C2 ways and number of permutations of such four letters is 4!/2!2!
Case II : When four letters consist of one similar pair and 2 different letters. We can choose such letters in 3C1 × 7C2 ways and then number of possible permutations is 4!/2!
Case III : When four letters consist of all different
letters. We can choose such letters in 8C4 ways and then
number of permutations is 4!.
∴ The required number of arrangements
= 3C2 x 4!/2!2! + 3C1 x 7C2 x 4!/2! + 8C4 × 4! = 2454
OR
A question paper contains 12 questions, divided into three parts. Part A contains 6 questions while B and C contains 3 questions each. A candidate is required to attempt 6 questions selecting at least two from part A and at least one from each of part B and part C. In how many ways can the candidate select 6 questions?
Answer: A candidate can select 6 questions in the following 6 ways :
(i) 2 from part A, 1 from part B and 3 from part C.
(ii) 2 from part A, 2 from part B and 2 from part C.
(iii) 2 from part A, 3 from part B and 1 from part C.
(iv) 3 from part A, 1 from part B and 2 from part C.
(v) 3 from part A, 2 from part B and 1 from part C.
(vi) 4 from part A, 1 from part B and 1 from part C.
∴ Required no. of ways = C(6, 2) · C(3, 1) · C(3, 3)
+ C(6, 2) · C(3, 2) · C(3, 2) + C(6, 2) · C(3, 3) · C(3, 1)
+ C(6, 3) · C(3, 1) · C(3, 2) + C(6, 3) · C(3, 2) · C(3, 1)
+ C(6, 4) · C(3, 1) · C(3, 1)
= 6×5/2 x 3/1 x 1+6×5/2 x 3/1 x 3/1 + 6×5/2 x 1×3
+ 6x5x4/6 x 3/1 x 3/1 + 6x5x4/6 x 3/1×3/1 + 6×5/2 x 3/1 x 3/1
= 45 + 135 + 45 + 180 + 180 + 135 = 720
19. Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse 36×2 + 4y2 = 144.
Answer: Given equation of the ellipse is
36×2 + 4y2 = 144 ⇒ x2/4 + y2/36 = 1
where a2 = 36 ⇒ a = 6, b2 = 4 ⇒ b = 2
Now, c2 = a2 – b2 = 36 – 4 = 32 ⇒ c = 4 2
Foci are (0, ± c) i.e., (0, ± 4 2)
Vertices are (0, ± a) i.e., (0, ± 6)
Length of major axis = 2a = 2 × 6 = 12
Length of minor axis = 2b = 2 × 2 = 4
Eccentricity, e = c/a = 4√2/6 = 2√2/3
Length of latus rectum = ab2/a = 2×4/6 = 4/3
OR
Find the equation of the parabola with vertex (2, – 3) and focus (0, 5).
Answer: In a parabola, vertex is the mid-point of the focus and the point of intersection of the axis and directrix. So, let (x1, y1) be the coordinates of the point of intersection of the axis and directrix. Then, (2, –3) is the mid-point of the line segment joining (0,5) and (x1, y1).
∴ x1+0/2 = 2 and y1+5/2 = − ⇒ x1 = 4, y1 = –11.
Thus, the directrix meets the axis at (4, –11).
Let A be the vertex and S be the focus of the required parabola. Then,
m1 = slope of AS = 5+3/0-2 = -4
Let m2 be the slope of the directrix. Then,
m1 m2 = –1 ⇒ m2 = -1/m1 = 1/4 .
Thus, the directrix passes through (4, –11) and has slope
1/4 . Therefore, the equation of the directrix is
y +11 = 1/4(x – 4) ⇒x − 4y − 48 = 0
Let P(x, y) be any point on the required parabola, and let PM be the length of the perpendicular from P on the directrix. Then,
SP = PM ⇒ SP2 = PM2
⇒ (x-0)2 + (y-5)2 = (x-4y – 48/√12+(-4)2)2
⇒ 17×2 + 17y2 – 170y + 425 = x2 + 16y2 + 2304
– 8xy – 96x + 384y
⇒ 16×2 + y2 + 8xy + 96x – 554y – 1879 = 0 is the required equation of parabola.


