Refer to below provided Class 10 Mathematics Sample Paper with solutions. These Guess papers for Mathematics Class 10 have been designed based on the latest examination guidelines and paper pattern issued by CBSE. We have provided all Sample Papers for Class 10 Mathematics with answers. You can click on the links below to access the practice papers for free.

CBSE Sample Papers for Class 10 Mathematics

Class 10 Mathematics Sample Paper Term 2 Set A

Class 10 Mathematics Sample Paper Term 2 Set A

SECTION – A

1. Find the discriminant of the quadratic equation 3x² − 2√2x − 2√3 = 0 .
Answer : The given equation is √3x² − 2√2x − 2√3 = 0.
Here, a = √3, b = − 2√2 and c = − 2√3
Now, D = b² – 4ac
D = (−2√2)² − 4 × √3 × (−2√3) = 8 + 24 = 32

OR

The sum of the squares of two consecutive natural numbers is 41. Represent this situation in the form of a quadratic equation.
Answer : Let the two consecutive natural numbers be x and x + 1.
Then, their squares are x² and (x +1)² respectively.
∴ The required equation is, x² + (x + 1)² = 41
⇒ x² + x² + 1 + 2x = 41
⇒ 2x² + 2x – 40 = 0 ⇒ x² + x – 20 = 00

2. Find the roots of the quadratic equation x² + 4√2x + 6 = 0.
Answer : We have, x² + 4√2x + 6 = 0
⇒ x² + 3√2 x + √2 x + 6 = 0
⇒ x(x + 3√2) + 2 (x + 3√2) = 0
⇒ (x + 2)(x + 3√2) = 0
⇒ x = − 2 or x = −3√2
∴ Roots are − 2 and − 3√2.

3. XY and MN are the tangents drawn at the end points of the diameter DE of the circle with centre O. Prove that XY || MN.

Answer : Since, XY is the tangent to the circle at the point D.
⇒ OD ⊥ XY ⇒ ∠EDX = 90°
Also, MN is the tangent to the circle at E.
⇒ OE ⊥ MN ⇒ ∠ DEN = 90°
As, ∠EDX = ∠DEN (each 90°)
which are alternate interior angles.
⇒ XY ||MN

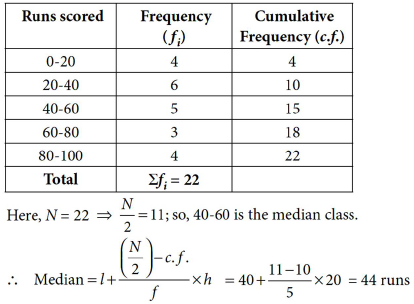
4. An inter house cricket match was organized by a school. Distribution of runs made by the students is given below. Find the median runs scored.

Answer : 

5. Find the common difference of the AP 4, 9, 14, … If the first term changes to 6 and the common difference remains the same then write the new AP.
Answer : Given A.P. is 4, 9, 14, …
So, common difference, d = 9 – 4 = 5
If the first term is 6 and common difference is 5, so new A.P. will be 6 , 6 + 5, 6 + 10, …
i.e., 6, 11, 16, …

6. Three cubes each of volume 64cm³ are joined end to end to form a cuboid. Find the total surface area of the cuboid so formed?
Answer : Let a be the side of each cube and l, b and h be the length, breadth and height of the cuboid.
Given, volume of cube = 64 cm³
⇒ a³ = 64 ⇒ a = 4 cm
Also, l = 3a = 12 cm, b = a = 4 cm and h = a = 4 cm
So, total surface area of cuboid = 2(lb + bh + hl)
= 2 (48 + 16 + 48)
= 224 cm2.

OR

The material of a cone is converted into the shape of a cylinder of equal radius. If height of the cylinder is 8 cm, then find the height of the cone.
Answer : Let r be the radius of cone & cylinder and h be the height of cone.
∵ Volume of cone = Volume of cylinder
∴ (1/3)πr²h = πr²(8) ⇒ h = 3 × 8 = 24 cm

SECTION – B

7. Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60⁰.
Answer : Steps of Construction :
1. Draw a circle of radius 5 cm with centre O.
2. Taking a point A on the circle draw ∠AOB = 120⁰.
3. Draw a perpendicular on OA at A.
4. Draw another perpendicular on OB at B.
5. Let the two perpendiculars meet at C .
Thus, CA and CB are the two required tangents to the given circle which are inclined to each other at 60⁰.

OR

Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm.
Answer : Steps of Construction :
1. Draw a circle with centre O and radius 4 cm.
2. Draw another circle with centre O and radius 6 cm.
3. Take a point P on outer circle and join OP.
4. Draw perpendicular bisector of OP which intersect OP at M.
5. Draw a circle with centre M which intersects inner circle at points A and B.
6. Join AP and BP. Thus AP and BP are required tangents.

8. Calculate the mode for the following frequency distribution

Answer : The frequency distribution table from the given data can be drawn as :

9. An aeroplane flying at a height of 9000 m from the ground passes vertically above another aeroplane at an instant, when the angles of elevation of the two planes from the same point on the ground are 60° and 30° respectively. Find the vertical distance between the aeroplanes at that instant.
Answer : Let A and B be the positions of two aeroplanes when A is vertically above B and AC = 9000 m.
Let D be the point of observation on the ground such that ∠ADC = 60° and ∠BDC = 30°.

10. Find ‘p’ if the mean of the given data is 15.45.

Answer : The frequency distribution table from the given data can be drawn as :

SECTION – C

11. A manufacturer of laptop produced 6000 units in 3rd year and 7000 units in the 7th year. Assuming that production increases uniformly by a fixed number every year, find
(i) the production in the 1st year,
(ii) the production in the 5th year,
(iii) the production in 6th year.
Answer : Let production in 1st year be a units and increase in production (every year) be d units.
Increase in production is constant.
∴ Unit produced every year forms an A.P.
Now, a3 = 6000 ⇒ a + 2d = 6000 ⇒ a = 6000 – 2d …(i)
and a7 = 7000 ⇒ a + 6d = 7000
⇒ (6000 – 2d) + 6d = 7000 [Using (i)]
⇒ 4d = 1000 ⇒ d = 250
Putting d = 250 in (i), we get a = 6000 –2 × 250 = 5500
(i) Production in first year = 5500
(ii) Production in fifth year, a5 = a + 4d = 5500 + 4 × 250 = 6500
(iii) Production in sixth year, a6 = a + 5d = 5500 + 5 × 250 = 6750

12. In the below figure, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29 cm, AD = 23 cm, ∠B = 90⁰ and DS = 5 cm, then find the radius of the circle (in cm).

Answer : Since length of tangents from an external point to a circle are equal,
DR = DS = 5 cm, AR = AQ and BQ = BP
Now AR = AD − DR = 23 − 5 = 18 cm
AQ = AR = 18 cm
QB = AB − AQ = 29 − 18 = 11 cm
PB = QB = 11
Now ∠OQB = ∠OPB = 90⁰ because radius is always perpendicular to tangent.
Thus OP = OQ = PB = BQ
So, POQB is a square. Hence, r = OP = PB = 11 cm

CASE STUDY QUESTION – 1

13. Mohan took 4 small spherical balls of silver of surface area 887.04 sq.cm each from a blacksmith. He wanted them to be made into cylindrical coins of radius one-fourth of that of the silver ball and height 4 cm.

(i) Find the radius of each spherical ball.
(ii) Find the curved surface area of each coin.
Answer : (i) Let r be the radius of a small spherical ball.
Surface area of a spherical ball = 887.04 cm²
⇒ 4πr² = 887.04
⇒ r = 8.4 cm
(ii) Radius of a cylindrical coin = (1/4) × 8.4 = 2.1 cm
and height of a cylindrical coin = 4 cm
Now, curved surface area of a coin = 2πrh
= 2 × 22/7 × 2.1 × = 52.8 cm²

CASE STUDY QUESTION – 2

14. A lighthouse is a tall tower with light near the top. These are often built on islands, coasts or on cliffs. Lighthouses on water surface act as a navigational aid to the mariners and send warning to boats and ships for dangers. Initially wood, coal would be used as illuminators. Gradually it was replaced by candles, lanterns, electric lights. Nowadays they are run by machines and remote monitoring. Prongs Reef lighthouse of Mumbai was constructed in 1874-75. It is approximately 40 meters high and its beam can be seen at a distance of 30 kilometres. A ship and a boat are coming towards the lighthouse from opposite directions. Angles of depression of flash light from the lighthouse to the boat and the ship are 300 and 600 respectively.

(i) Which of the two, boat or the ship is nearer to the light house. Find its distance from the lighthouse?
(ii) Find the time taken by the boat to reach the light house if it is moving at the rate of 2 km per hour.
Answer :