Class 12 Mathematics Sample Paper Set D
Please see below Class 12 Mathematics Sample Paper Set D with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.
CBSE Sample Paper for Class 12 Mathematics Set D
SECTION – A
1. Find the sum of the order and degree of the given differential equation : d/dx[(d2y/dx2)4] = 0 .
Solution : Given d/dx[(d2y/dx2)4] = 0 ⇒ 4(d2y/dx2)3 x d3y/dx3 = 0 .
Since order and degree of the differential equation is 3 and 1 respectively. So their sum is 4.
2. Find the integrating factor of x log x dy/dx + y = 2 log x .
Solution : We’ve x log x dy/dx + y = 2 ⇒ dy/dx + 1/x log x , y = 2/x
Here P(x) = 1/x log x , Q(x) = 2/x

3. Find the value of (x + y) from the following matrix equation :

Solution :
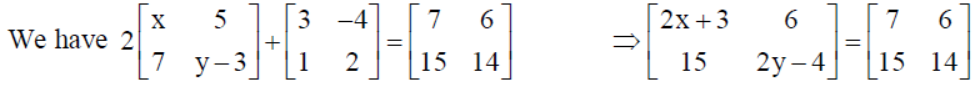
By equality of matrices, we get : 2x + 3 = 7, 2y – 4 =14 ⇒ x = 2, y = 9 .
Hence (x + y) = 2 + 9 =11.
4. If |a̅| = a , then find the value of : |a̅ x î|2 + |a̅ x ĵ|2 + |a̅ x k̂|2
Solution :

5. Find the angle θ , between the line x-2/3 = y-3/5 = z-4/4 and the plane 2x – 2y + z – 5 = 0 .
Solution : The d.r.’s of the given line x-2/3 = y-3/5 = z-4/4 is 3, 5, 4 ∴ b̅ = 3î + 5ĵ + 4k̂.
Also the d.r.’s of the normal to the plane 2x – 2y + z – 5 = 0 is 2, –2, 1 ∴ m̅ = 2î – 2ĵ + k̂ .

6. The vectors a̅ = 3î + xĵ and b̅ = 2î + ĵ + yk̂are mutually perpendicular. If |a̅| = |b̅| , then find the value of y.
Solution :


SECTION – B
7. Find :

Solution :

8. Find :

Solution :

9. Find a unit vector perpendicular to the plane of triangle ABC, where the coordinates of its vertices are A(3, –1, 2), B(1, –1, –3) and C(4, –3, 1).
Solution : Given vertices of triangle ABC are A(3, –1, 2), B(1, –1, –3) and C(4, –3, 1).

10. Find the shortest distance between the lines x + 1= 2y = -12z and x = y + 2 = 6z – 6 .
Solution : Given lines are L1 : x + 1 = 2y = – 12z i.e., x-(-1)/1 = y-0/1/2 = z-0/-1/2 or x-(-1)/12 = y-0/6 = 0/-1
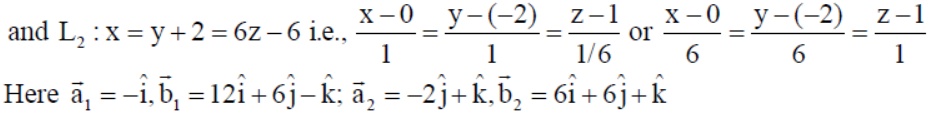

OR
From the point P(a, b, c), perpendiculars PL and PM are drawn to YZ and ZX planes respectively. Find the equation of the plane OLM.
Solution : Since perpendiculars PL and PM are drawn to the planes YZ and ZX respectively from P(a, b, c). So the coordinates of L and M on required plane OLM are L (0, b, c) and M (a, 0, c).
Also we know that O (0, 0, 0).

Expanding along R1, we get : bcx + acy – abz = 0 or, x/a + y/b – z/c = 0
11. In 3 trials of a binomial distribution, the probability of exactly 2 successes is 9 times the probability of 3 successes. Find the probability of success in each trial.
Solution : Let p : probability of success and q : probability of failure. Also n = 3.

Therefore the probability of success in each trial is 1/4 .
OR
An urn contains 3 red and 5 black balls. A ball is drawn at random, its colour is noted and returned to the urn. Moreover, 2 additional balls of the colour noted down, are put in the urn and then two balls are drawn at random (without replacement) from the urn. Find the probability that both the balls drawn are of red colour.
Solution : Let E : both the balls drawn are of red colour, E1 : red ball is drawn in first attempt and E2 : black ball is drawn in the first attempt.
Case I : A red ball is drawn in the first attempt. ∴ P(E1) = 3/8
If 2 red balls are added to the urn, then the urn contains 5 red and 5 black balls.
Then, P(E|E1) = 5/10 x 4/9 = 20/90
Case II : A black ball be drawn in the first attempt. ∴ P(E2) = 5/8
If 2 black balls are added to the urn, then the urn contains 3 red and 7 black balls.
Then, P(E|E1) = 3/10 x 2/9 = 6/90
Therefore required probability, P(E) = P(E1) P(E|E1) + P(E|E2) = 3/8 x 20/90 + 5/8 x 6/90 = 1/8 .
12.

Solution :

13. Let f (x) = x – | x – x2 |, x∈[-1, 1] . Find the point of discontinuity, (if any), of this function on [-1, 1] .
Solution :
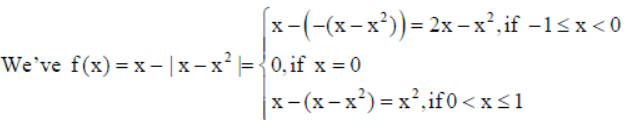
Since the function f (x) is a polynomial function and is continuous on [-1,0]∪[0,1] . That is, f (x) has one turning point (x = 0) in [–1, 1] so, we’ll check its continuity at x = 0.
Continuity at x = 0 : We have f (0) = 02 = 0

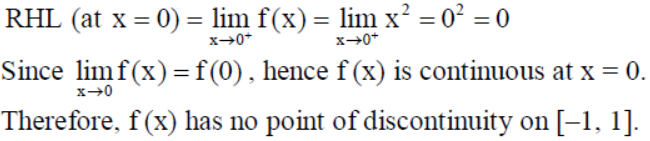
14.
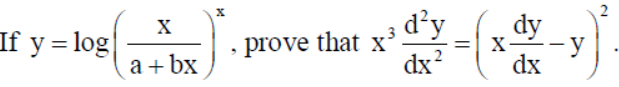
Solution :

15. Find the derivative of sec-1(1/2x2-1) w.r.t. √1-x2 at x = 1/2 .
Solution :

16. Evaluate :

Solution :


∴ I = 2π .
OR
Evaluate :

Solution :
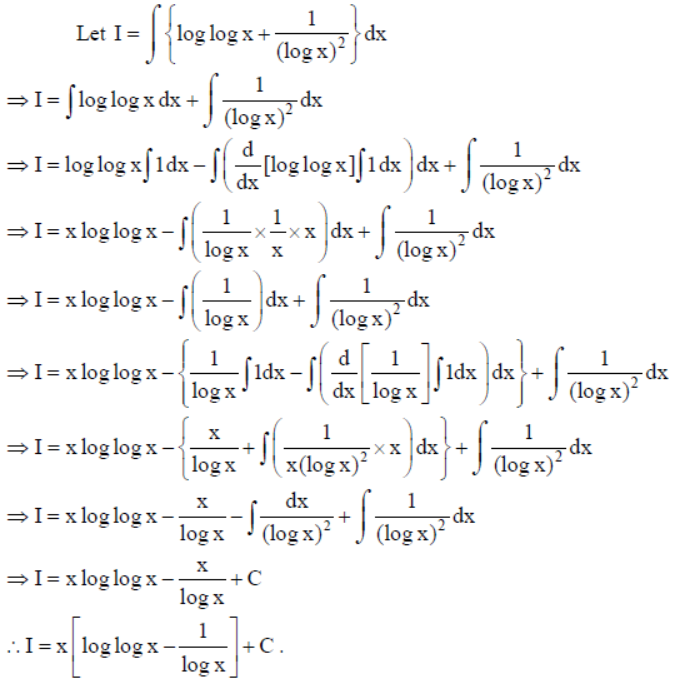
17. A trust caring for handicapped children gets ₹30000 every month from its donors. The trust spends half of the funds received for medical and educational care of the children and for that it charges 2% of the spent amount from them, and deposits the balance amount in a private bank to get the money multiplied so that in future the trust goes on functioning regularly. What percent of interest should the trust get from the bank to get a total of ₹1800 every month?
Use matrix method, to find the rate of interest.
Do you think people should donate to such trusts?
Solution : Let the rate of interest at which the half of the amount ₹30000 is deposited in the bank be x %.

Hence the required rate of interest is 10%.
Yes, people should donate to the trusts which are involved in the service of society.
18. Find the value of x, if sin[cot-1(x+1)] = cos(tan-1x) .
Solution : We have sin[cot-1(x +1)] = cos(tan-1 x) ⇒ sin sin-1 1/√1+(x+1)2 = cos cos-1 1/√1+x2
⇒ 1/√1+(x+1)2 = 1/√1+x2 ⇒ 1+x2 = 1+x2 + 2x + 1
∴ x = -1/2
OR
Prove that : 2sin-1 3/5 – tan-1 17/31 = π/4 .
Solution : LHS : 2sin-1 3/5 – tan-1 17/31 = 2tan-1 3/4 – tan-1 17/31

19. If a + b + c ≠ 0 and
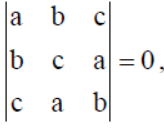
then using properties of determinants, prove that a = b = c .
Solution :


SECTION – C
20. Suppose a boy throws a die. If he gets a 1 or 2, he tosses a coin three times and notes down the number of ‘heads’. If he gets 3, 4, 5 or 6, he tosses the coin once and notes down whether a head or tail is obtained. If he obtains exactly one head, what is the probability that he obtained 3, 4, 5 or 6 with the die?
Solution : Let A : getting 1 or 2, B : getting 3, 4, 5 or 6, E : getting exactly one head.
So, P(A) = 2/6, P(B) = 4/6,

OR
A man is known to speak the truth 3 out of 5 times. He throws a die and reports that it is 4. Find the probability that it is actually a 4.
Solution : Let A : the man reports that 4 occurs, E : 4 actually occurs.

21. A dealer in rural area wishes to purchase some sewing machines. He has only ₹57600 to invest and has space for at most 20 items. An electronic machine costs him ₹3600 and a manually operated machine costs ₹2400. He can sell an electronic machine at a profit of ₹220 and a manually operated machine at a profit of ₹180. Assuming that he can sell all the machines that he buys, how should he invest his money in order to maximize his profit? Make it as a LPP and solve it graphically.
Solution : Let the number of electronic operated machine be x and the number of manually operated sewing machines be y.

To maximize: Z = ₹(22x + 18y)
Subject to constraints : x + y ≤ 20 …(i)
3600x + 2400y ≤ 57600 i.e., 3x + 2y ≤ 48 …(ii) x ≥ 0, y ≥ 0 .
Corner points of the feasible region are A(0, 20), P(8, 12), B(16, 0) and O(0, 0).
Now, ZA = ₹3600, ZB = ₹3520, ZP = ₹3920, ZO = ₹ 0.
∴ Z is maximum at x = 8 and y = 12. Also maximum profit is ₹3920.
The dealer should invest in 8 electronic and 12 manually operated machines.
22. On the set {0, 1, 2, 3, 4, 5, 6}, a binary operation * is defined as : a*b =
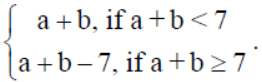
Write the operation table of the operation * and prove that zero is the identity for this operation and each element a ≠ 0 of the set is invertible with ‘7 – a’ being the inverse of ‘a’.
Solution : We have a*b =
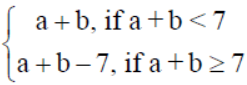
defined on the set A = {0, 1, 2, 3, 4, 5, 6}.
Operation table of the binary operation * is given below :

Let x be the identity for an element a.
So a * x = a . If a + x < 7 then, a + x = a or if a + x ≥ 7 then, a + x – 7 = a
That is, a + x < 7 then, x = 0 ∈ A or if a + x ≥ 7 then, x = 7 ∉ A
Therefore, x = 0 is the identity element for this operation.
Also let y be the inverse of each non-zero element a. Then a * y = 0 .
If a + y < 7 then, a + y = 0 or if a + y ≥ 7 then, a + y – 7 = 0
i.e., a + y < 7 then, y = -a ∉ A for all a ∈ A or if a + y ≥ 7 then, y = 7 – a ∈ A for all a ∈ A -{0}
∴ y = 7 – a is the inverse of each non-zero element a .
23. Find the maximum area of an isosceles triangle inscribed in the ellipse x2/16 + y2/9 = 1 with its vertex at one end of the major axis.
Solution : We have the equation of ellipse as : x2/16 + y2/9 = 1
Let ABC be an isosceles triangle whose one vertex is at the A(4, 0).
Let the coordinates of B be (4cosθ,3sin θ) .
Then the coordinates of C will be (4cosθ,- 3sin θ) .
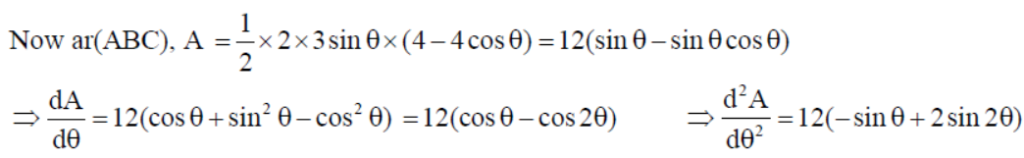


24. Given that (x2 + y2 )dy = xydx . If y(1) =1 and y(x0) = e, then find the value of x0 .
Solution : We have (x2+y2) dy = xydx ⇒ dy/dx = xy/x2+y2

OR
Find the particular solution of the differential equation dy/dx + y tan x = 3x2 + x3 tan x, x ≠ π/2 , given that y = 0 when x = π/3 .
Solution : Given that dy/dx + y tan x = 3x2 + x3 tan x, x ≠ π/2 .
This is linear differential equation of the form dy/dx + yP(x) = Q(x) , where P(x) = tan x and Q(x) = 3x2 + x3 tan x .

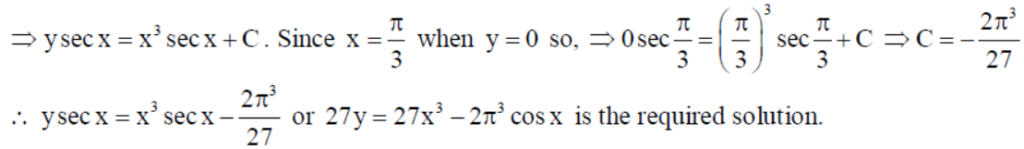
25. Find the coordinates of the point where the line through the points A(3, 4, 1) and B(5, 1, 6) crosses the plane determined by the points P(2, 1, 2), Q(3, 1, 0) and R(4, –2, 1).
Solution : Equation of the line joining the points A(3, 4, 1) and B(5, 1, 6) is :

Coordinates of any random point on this line is M(2λ + 3,-3λ + 4,5λ +1) .
Also the equation of plane through the points P(2, 1, 2), Q(3, 1, 0) and R(4, –2, 1) is :
Expanding along R1, we get :
⇒ -6(x – 2) – 3(y -1) -3(z – 2) = 0 ⇒ 2(x – 2) + (y -1) + (z – 2) = 0 ⇒ 2x + y + z = 7
When the line obtained above crosses the plane 2x + y + z = 7 , we’ve :
2(2λ + 3) + (-3λ + 4) + (5λ + 1) = 7 ∴ λ = -2/3
So, M (5/3,6,-7/3)
Hence the coordinates of the required point are (5/3 , 6 , -7/3) .
26. Find the area of the region {(x, y) : x2 + y2 ≤ 4, x + y ≥ 2}, using the method of integration.
Solution : We have {(x, y) : x2 + y2 ≤ 4, x + y ≥ 2}
Let x2 + y2 = 4…(i) and x + y = 2…(ii)
On solving (i) & (ii) we get the point of intersection as (0, 2) and (2, 0).
Now, the area of the shaded region bounded by


