Please see below Class 12 Mathematics Sample Paper Set J with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.

CBSE Sample Paper for Class 12 Mathematics Set J

SECTION – A

1. Find the value of tan⁻¹√3 −sec⁻¹(−2) .
Sol. tan⁻¹√3 sec⁻¹(2) = tan⁻¹ tan π/3 sec−1 sec 2π/3 = π/3 − 2π/3 = −π/3.

2.

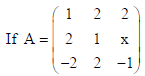
is matrix satisfying AA’ = 9I , find x.
Sol. 

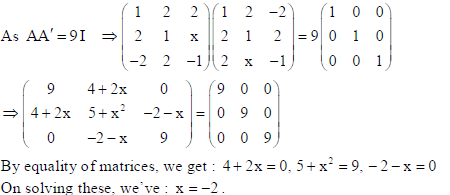
3. Find the value of [î k̂, ĵ].
Sol. [î k̂, ĵ] = î.(k̂ × ĵ) = î.(−î) = −1.

4. Find the identity element in the set Q⁺ of all positive rational numbers for the operation * defined by a *b = 3ab/2  for all a, b ∈ Q⁺.
Sol. Let e ∈ Q⁺ be the identity element so, we have a *e = a ⇒ 3ae/2 = a ⇒ e = 2/3.

SECTION – B

5. Prove that 3cos⁻¹ x = cos⁻¹ (4x³ − 3x), x ∈ [1/2 , 1]
Sol. In RHS, put x = cos θ ⇒ θ = cos⁻¹ x .
Also, as 1/2 ≤ x ≤ 1    ⇒ 1/2  ≤ cosθ ≤1    ⇒  0 ≤ θ ≤ π/3    ⇒ 0 ≤ 3θ ≤ π
Now, RHS: cos⁻¹(4x³ −3x) = cos⁻¹(4cos³θ −3cosθ) = cos⁻¹ cos3θ = 3θ = 3cos⁻¹ x = LHS.

6.

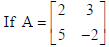
be such that A⁻¹ = kA, then find the value of k.
Sol. 

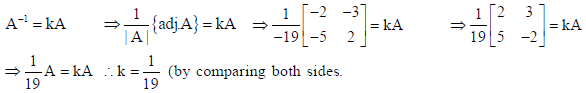
7. Differentiate 

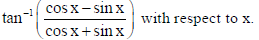
Sol.

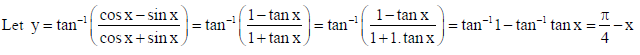
On differentiating w.r.t. x both sides, we get : dy/dx = 0 − 1 =  −1

8. The total revenue received from the sale of x units of a product is given by R(x) = 3x² + 36x + 5 in rupees. Find the marginal revenue when x = 5 , where by marginal
revenue we mean the rate of change of total revenue with respect to the number of items sold at an instant.
Sol. R(x) = 3x² + 36x + 5 ⇒ MR = d/dx [R(x)] = 6x + 36
When x = 5 , then MR = 6×5 + 36 = 66 in rupees.

9. Find :

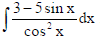
Sol.

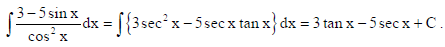
10. Solve the differential equation cos (dy/dx) = a, (a ∈ R )
Sol. cos (dy/dx) = a  ⇒ dy/dx = cos ⁻¹a        ⇒ ∫dy = ∫cos ⁻¹adx   ⇒ y = (cos⁻¹ a) x +C.

11. If a̅ + b̅ + c̅ = 0 and a̅ = 5, b̅ = 6 and c̅ = 9 then find the angle between a̅ and b̅. 
Sol. Let θ be the required angle betweena̅ and b̅.
Now a̅ + b̅ + c̅ = 0     ⇒  a̅ + b̅ = −c̅       ⇒ |a̅ + b̅| = |−c̅| = |c̅|  ⇒ |a̅ + b̅|² = |c̅|²
⇒ (a̅ + b̅).(a̅ + b̅) = c̅.c̅           ⇒  a² + 2a̅ .b̅ + b² = c²      ⇒ 25 + 2ab cosθ + 36 = 81
⇒ 2×5×6cos θ = 20               ⇒ 2 × 5 × 6 cosθ = 20     ⇒ cos θ = 20/60 = 1/3       ∴ θ = cos ⁻¹1/3 .

12. Evaluate P(A ∪ B), if 2P(A) = P(B) = 5/13  and P(A | B) = 2/5
Sol.

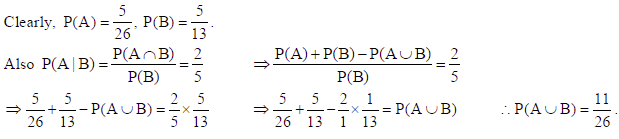
SECTION – C

13. Using properties of determinants, prove that

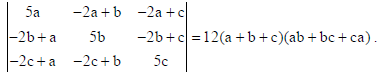
Sol.

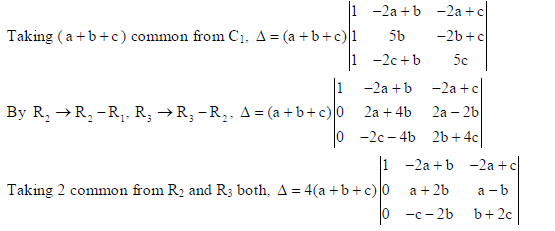
Now expanding along C₁, Δ = 4(a + b + c){1[(a + 2b)(b + 2c) − (a − b)(−c − 2b)]− 0 + 0}
⇒ Δ = 4(a + b + c){ab + 2ac + 2b2 + 4bc + ac + 2ab − bc − 2b²}
⇒ Δ = 4(a + b + c){3ab + 3bc + 3ac} =12(a + b + c)(ab + bc + ca) = RHS .

14. 

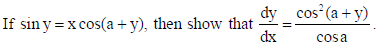
Also, show that dy/dx = cos a, when x = 0.
Sol.

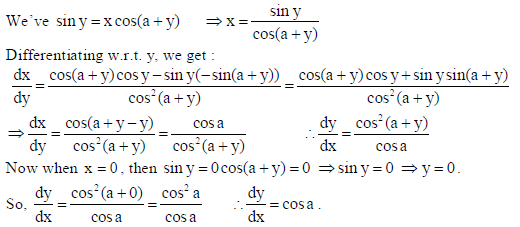
15. If x = a sec³ θ and y = a tan³ θ , then find d²y/dx² at θ = π/3.
Sol. Here x = a sec³ θ and y = a tan³ θ     ⇒ dx/dθ = 3a sec³ θ tan θ and dy/dθ = 3a tan² θ sec²θ 

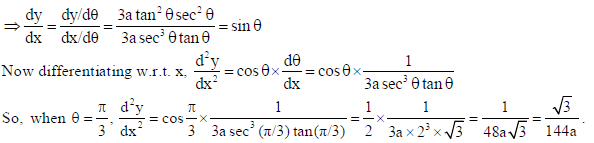
OR

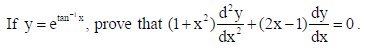
Sol.  

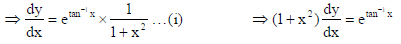
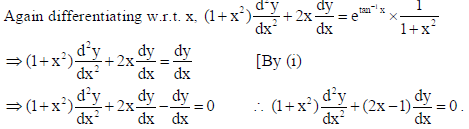
16. Find the angle of intersection of the curves x² + y² = 4 and (x − 2)² + y² = 4 , at the point in the first quadrant.
Sol. We have x² + y² = 4 and (x − 2)² + y² = 4 …(ii)
On solving (i) and (ii), we get : x² − 4x + 4 + y² = 4       ⇒ x =1      ∴ y = ± √3 .
So, the points of intersection are P(1, √3) and Q(1,− √3) .
As we have to find the angle of intersection in the first quadrant so, we shall take only point

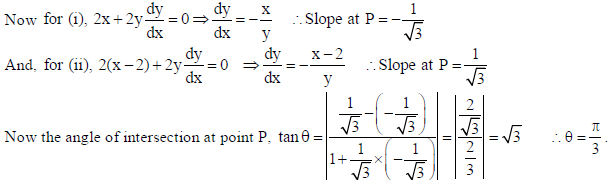
OR

Find the intervals in which the function f (x) = −2x³ −9x² −12x +1 is
(i) Strictly increasing (ii) Strictly decreasing.
Sol. Given f (x) = −2x³ −9x² −12x +1     ⇒  f ‘(x) = −6x² −18x −12 = −6(x +1)(x + 2)
For critical points, f ‘(x) = −6(x +1)(x + 2) = 0 ∴x = −1,−2

So, clearly f (x) is Strictly decreasing in (−∞,−2)∪(−1, ∞) and Strictly increasing in (−2,−1) .

17. A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 metres. Find the dimensions of the window to admit maximum light through the whole opening. How having large windows help us in saving electricity and conserving environment?
Sol. Let ABCD be a rectangle and let the semi-circle is described on the side AB as its diameter.

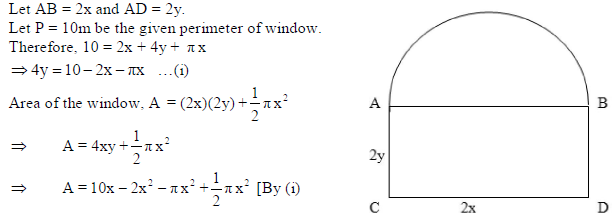
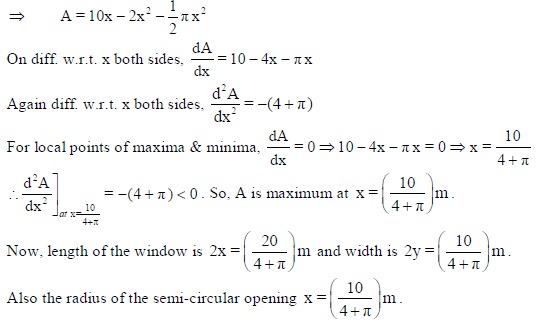
18. Find

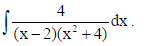
Sol. 

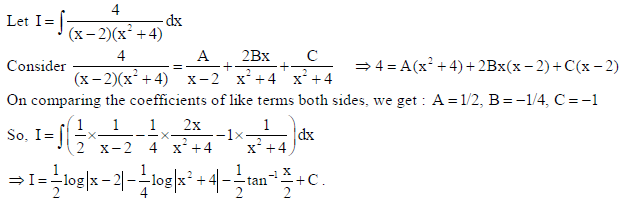
19. Solve the differential equation (x² − y² )dx + 2xydy = 0 .
Sol.   

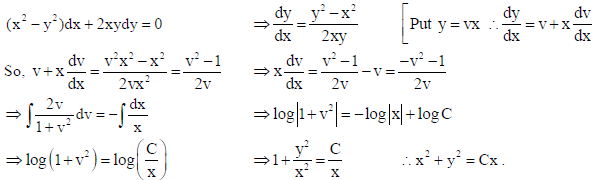
OR

Find the particular solution of the differential equation (1+x²) dy/dx + 2xy = 1/1+x² given
that y = 0 when x =1.
Sol.

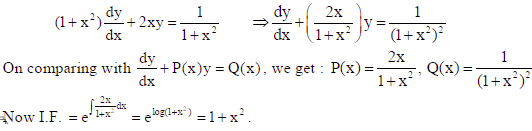
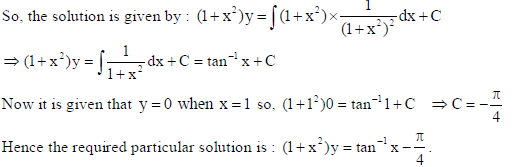
20. Find x such that the four points A(4, 4, 4), B(5, x, 8), C(5, 4, 1) and D(7, 7, 2) are coplanar.
Sol. Let A(4î + 3ĵ+ 3k̂ ) , B(5î + xĵ+ 7k̂ ) , C(5î + 3ĵ) and D(7î + 6ĵ+ k̂ )

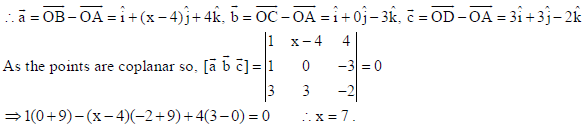
⇒ 1(0 + 9) − (x − 4)(−2+ 9) + 4(3− 0) = 0    ∴ x = 7 .

21. Find the shortest distance between the lines 

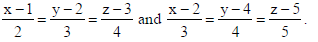
Sol. Writing lines in the vector form : r̅ = î + 2ĵ+ 3k̂ + λ(2iˆ + 3ĵ+ 4k̂ ) and
r̅ = 2î + 4ĵ+ 5k̂ + μ(3î + 4ĵ+ 5k̂)
So, we have  a̅₁ = î + 2ĵ+ 3k̂, b̅₁  = 2î + 3ĵ+ 4k̂  a̅₂ = 2î + 4ĵ+ 5k̂, b̅₂ = 3î + 4ĵ+ 5k̂ . 
∴  a̅₂ − a̅₁ = î + 2ĵ+ 2k̂ .

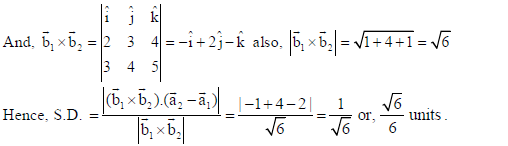
22. Two groups are competing for the position of the Board of Directors of a corporation. The probabilities that the first and second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product introduced was by the second group.
Sol. Let E₁, E₂ denote the events that first group and second group wins, respectively. Also, let E
denotes that the new product is introduced.
Here P(E₁) = 0.6, P(E₂) = 0.4, P(E|E₁) = 0.7, P(E|E₂) = 0.3.

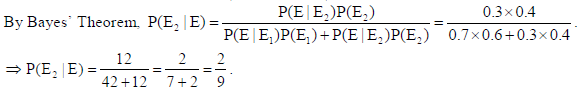
23. From a lot of 20 bulbs which include 5 defectives, a sample of 3 bulbs is drawn at random, one by one with replacement. Find the probability distribution of the number of defective bulbs. Also, find the mean of the distribution.
Sol. Let X : no. of defective bulbs. So, X = 0, 1, 2, 3.
Total bulbs = 20, and defective bulbs = 5

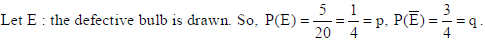
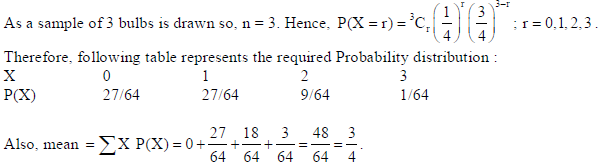
SECTION – D

24. Show that the relation R on the set Z of all integers defined by (x, y) ∈ R ⇔(x − y) is divisible by 3, is an equivalence relation.
Sol. We’ve relation R defined on Z as, (x, y) ∈ R ⇔(x − y) is divisible by 3.That is, R = {(x, y) :3 divides x − y} defined on Z.
R is reflexive, as 3 divides (x – x) i.e., 0 for all x ∈ Z. That is, x R x for all x ∈ Z.
Further if (x, y) ∈ R for all x, y ∈ Z, then 3 divides (x – y). Therefore, 3 divides (y – x) as well.
Hence, (y, x) ∈ R, which follows that R is symmetric.
Similarly, if (x, y) ∈ R and (y, z) ∈ R, then (x – y) and (y – z) are both divisible by 3.
That is, x − y = 3p, y − z = 3m where p, m ∈ Z.
Note that, x – z = (x – y) + (y – z) = 3p + 3m = 3 (p + m). So, (x – z) is divisible by 3.
This shows that R is transitive as (x, z) ∈ R.
Thus, R is an equivalence relation in Z.

OR

A binary operation * on the set A = {0, 1, 2, 3, 4, 5} is defined as

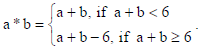
Write the operation table for a * b in A.
Show that zero is the identity for this operation * and each element ‘a’ ≠ 0 of the set is
invertible with 6 – a, being the inverse of ‘a’.
Sol.

Let x be the identity for an element a.
So a * x = a . If a + x < 6 then, a + x = a or if a + x ≥ 6 then, a + x − 6 = a
That is, a + x < 6 then, x = 0∈A or if a + x ≥ 6 then, x = 6 ∉ A
Therefore, x = 0 is the identity element for this operation.
Also let y be the inverse of each non-zero element a. Then a * y = 0 .
If a + y < 6 then, a + y = 0 or if a + y ≥ 6 then, a + y − 6 = 0
i.e., a + y < 6 then, y = −a ∉ A for all a ∈ A −{0}
Or, if a + y ≥ 6 then, y = 6 − a ∈ A for all a ∈ A−{0}
∴y = 6 − a is the inverse of each non-zero element a of A .

25. 

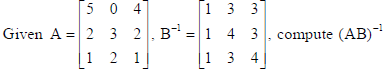
Sol.

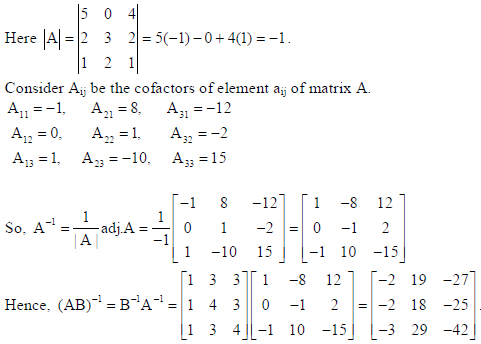
OR

Find the inverse of the matrix

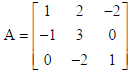
by using elementary row transformation. 
Sol. In row operations, we have A = IA 

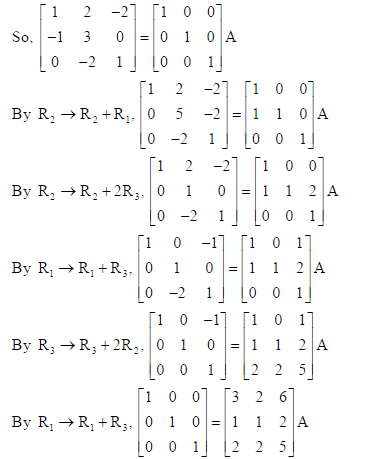
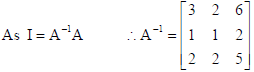
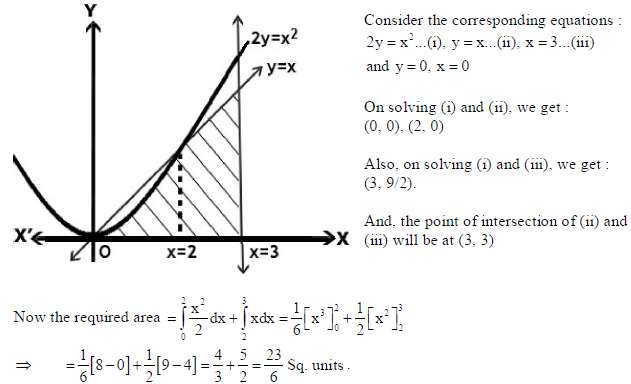
26. Using integration, find the area of region : {(x, y) : 0 ≤ 2y ≤ x² , 0 ≤ y ≤ x, 0 ≤ x ≤ 3}.
Sol. Consider the diagram shown below.

27. Evaluate

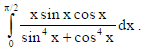
Sol. 

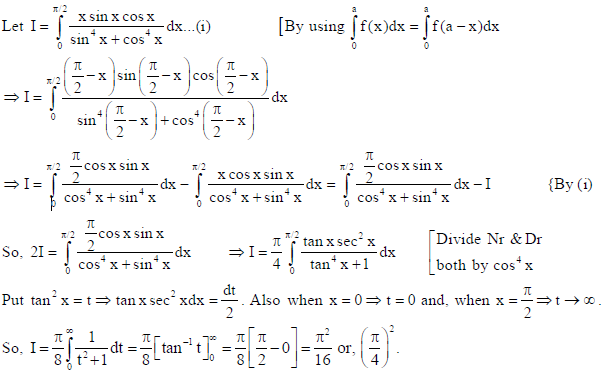
OR

Evaluate  

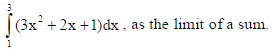
Sol.

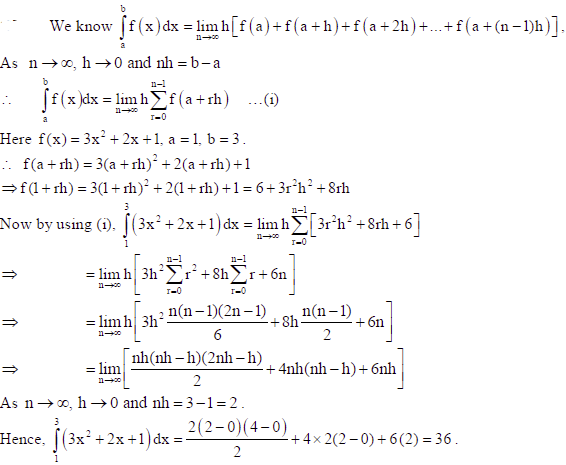
28. Find the vector equation of the line passing through (1, 2, 3) and parallel to each of the planes r̅.(î − ĵ+ 2k̂) = 5 and r̅.(3iˆ + ĵ+ k̂ ) = 6 . Also find the point of intersection of the line thus obtained with the plane r̅.(2î + ĵ+ k̂ ) = 4 .
Sol. 

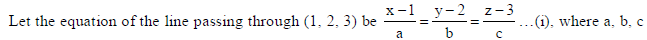
are d.r.’s of the required line.
This line is parallel to the planes r̅.(î − ĵ+ 2k̂) = 5 and r̅.(3iˆ + ĵ+ k̂ ) = 6 . So, clearly, the normals
of these two planes will be perpendicular to the line (i).
Therefore, a − b + 2c = 0 and 3a + b + c = 0

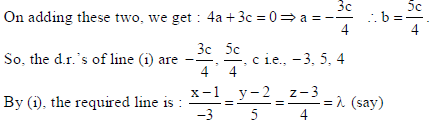
Hence, the vector eq. is : r̅ = î + 2ĵ+ 3k̂ + λ(−3î + 5ĵ+ 4k̂) .
Now consider the random point on line (i) as : P(−3λ +1, 5λ + 2, 4λ + 3) . For the intersection of
line and the plane r̅.(2î + ĵ+ k̂ ) = 4 i.e., 2x + y + z = 4 , point P must satisfy the eq. of plane.
So, 2(−3λ +1) + (5λ + 2) + (4λ + 3) = 4 ⇒ λ = −1
Hence the point of intersection is P(4, –3, –1).

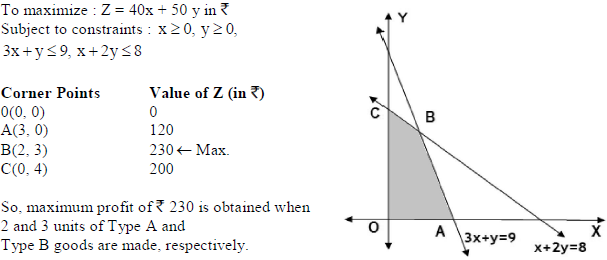
29. A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of gold while that of B requires 1 g of silver and 2 g of gold. The company can use at most 9 g of silver and 8 g of gold. If each unit of type A brings a profit of Rs 40 and that of type B Rs 50, find the number of units of each type that the company should produce to maximize the profit. Formulate and solve graphically the LPP and find the maximum profit.
Sol. Let x and y number of units of type A and type B goods are produced.