Class 12 Mathematics Sample Paper Set N
Please see below Class 12 Mathematics Sample Paper Set N with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.
CBSE Sample Paper for Class 12 Mathematics Set N
1. The equation of a tangent to the hyperbola 4x2-5y2=20 parallel to the line x – y = 2 is
(a) x – y – 3 = 0
(b) x – y + 9 = 0
(c) x – y + 1 = 0
(d) x – y + 7 = 0
Answer
C
2. Consider a triangular plot ABC with sides AB = 7 m, BC = 5 m and CA = 6 m. A vertical lamp-post at the mid-point D of AC subtends an angle 30° at B. The height (in m) of the
lamp-post is
(a) 2/3√21
(b) 2√21
(c) 7√3
(d)3/2√21
Answer
A
3.
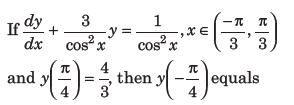
(a)1/3+ e6
(b) – 43
(c)13+ e3
(d)13
Answer
A
4.

Answer
C
5.
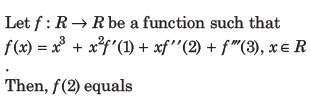
(a) 30
(b) – 4
(c) – 2
(d) 8
Answer
C
6. If the parabolas y2=4b(x-c) and y2 = 8ax have a common normal, then which one of the following is a valid choice for the ordered triad (a, b, c) ?
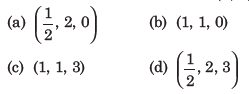
Answer
C
7. Let z1 and z2 be any two non-zero complex numbers such that
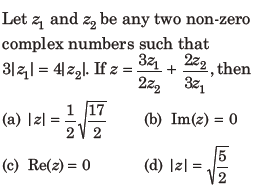
Answer
A
8. A point P moves on the line 2x – 3y + 4 = 0. If Q(1, 4) and R(3, – 2) are fixed points, then the locus of the centroid of ΔPQR is a line
(a) with slope 2/3
(b) with slope 3/2
(c) parallel to Y-axis
(d) parallel to X-axis
Answer
A
9. Consider the statement : ‘‘ P(n) : n2 – n+ 41 is prime.’’ Then, which one of the following is true?
(a) Both P(3) and P(5) are true.
(b) P(3) is false but P(5) is true.
(c) Both P(3) and P(5) are false.
(d) P(5) is false but P(3) is true.
Answer
A
10.
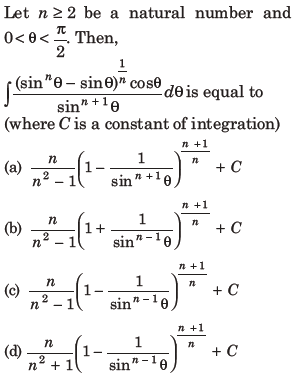
Answer
C
11.
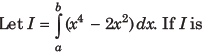
minimum, then the ordered pair (a, b) is
(a) (- 2, 0)
(b) (0, 2)
(c) ( 2, – 2)
(d) (- 2, 2)
Answer
D
12. The sum of all two digit positive numbers which when divided by 7 yield 2 or 5 as remainder is
(a) 1256
(b) 1465
(c) 1356
(d) 1365
Answer
C
13. An unbiased coin is tossed. If the outcome is a head, then a pair of unbiased dice is rolled and the sum of the numbers obtained on them is noted. If the toss of the coin results in tail, then a card from a well-shuffled pack of nine cards numbered 1, 2, 3, …, 9 is randomly picked and the number on the card is noted. The probability that the noted number is either 7 or 8 is
(a) 15/72
(b)13/36
(c)19/72
(d)19/36
Answer
C
14. If a circle C passing through the point (4, 0) touches the circle x2+y2+4x-6y=12 externally at the point (1, – 1), then the radius of C is
(a) 5
(b) 2 5
(c) 57
(d) 4
Answer
A
15. In a class of 140 students numbered 1 to 140, all even numbered students opted Mathematics course, those whose number is divisible by 3 opted Physics course and those whose number is divisible by 5 opted Chemistry course. Then, the number of students who did not opt for any of the three courses is
(a) 42
(b) 102
(c) 38
(d) 1
Answer
C
16. If the third term in the binomial expansion of (1+x log2x)5 equals 2560, then a possible value of x is
(a) 4 √2
(b)1/4
(c)1/8
(d) 2 /2
Answer
B
17. If the system of equations
x + y + z = 5
x + 2y + 3z = 9
x + 3y + az = β
has infinitely many solutions, then β – α equals
(a) 8
(b) 18
(c) 21
(d) 5
Answer
A
18.
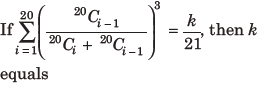
(a) 100
(b) 400
(c) 200
(d) 50
Answer
A
19. If the area enclosed between the curves y = kx2 and x = ky2, (k >0), is 1 square unit. Then, k is
(a) √3
(b)1/3
(c)2/3
(d)3/2
Answer
B
20. If the line 3x + 4y – 24 = 0 intersects the X-axis at the point A and the Y-axis at the point B, then the in centre of the triangle O AB, where O is the origin, is
(a) (4, 3)
(b) (3, 4)
(c) (4, 4)
(d) (2, 2)
Answer
D
21. The mean of five observations is 5 and their variance is 9.20. If three of the given five observations are 1, 3 and 8,then a ratio of other two observations is
(a) 4 : 9
(b) 6 : 7
(c) 10 : 3
(d) 5 : 8
Answer
A
22. Consider the quadratic equation
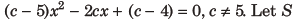
be the set of all integral values of c for which one root of the equation lies in the interval (0, 2) and its other root lies in the interval (2, 3). Then, the number of elements in S is
(a) 11
(b) 10
(c) 12
(d) 18
Answer
A
23.
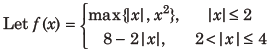
Let S be the set of points in the interval (-4, 4) at which f is not differentiable. Then, S
(a) equals {-2, – 1, 0, 1, 2}
(b) equals {-2, 2}
(c) is an empty set
(d) equals {-2,-1, 1, 2}
Answer
A
24. Let A be a point on the line///24 and B(3, 2, 6) be a point in the space.
Then, the value of m for which the vector AB is parallel to the plane x – 4y + 3z = 1is
(a)1/4
(b) – 1/4
(c)1/8
(d)1/2
Answer
A
25. Let d ∈ R, and
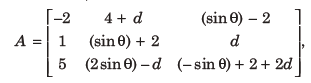
q ∈[θ, 2π]. If the minimum value of det (A) is 8, then a value of d is
(a) -5
(b) -7
(c) 2( √2 + 1)
(d) 2( √2 + 2)
Answer
A
26. If 5 5r, 5r2 are the lengths of the sides of a triangle, then r cannot be equal to
(a)5/4
(b)7/4
(c)3/2
(d)3/4
Answer
B
27. The sum of all values of θ ∈(0,π/2) satisfying sin2 2θ+cos42θ=3/4 is
(a)3π/8
(b)5π/4
(c)π/2
(d) π
Answer
C
28. The plane passing through the point
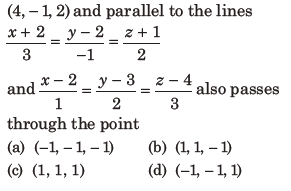
(a) (-1, – 1, – 1)
(b) (1, 1, – 1)
(c) (1, 1, 1)
(d) (-1, – 1, 1)
Answer
C
29. The shortest distance between the point(3/2,0) and the curve y = √x, (x > 0), is
(a)3/2
(b)5/4
(c)3/2
(d)5/2
Answer
D
30. For each t ∈R, let [t]be the greatest integer less than or equal to t. Then,
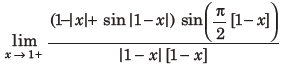
(a) equals 0
(b) does not exist
(c) equals – 1
(d) equals 1
Answer
A
