Please see below Class 12 Mathematics Sample Paper Term 1 Set C with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Term 1 Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.

CBSE Sample Paper for Class 12 Mathematics Term 1 Set C

Section A

1. – 17mod4 is
(a) 1
(b) – 1
(c) 3
(d) – 3

2. The smallest non-negative integer congruent to 2796 (mod 7) is
(a) 1
(b) 2
(c) 5
(d) 3

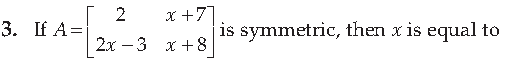
(a) 1
(b) 10
(c) 5
(d) 4

(a) 1/2
(b) – 1/2
(c) 1/3
(d) – 1/3

5. The slope of tangent of the curve y = √x at x = 9 is
(a) 1/2
(b) 1/3
(c) 1/9
(d) 1/6

6. The interval in which f (x) = – x² – x + 2 15 is increasing, is
(a) (- 1, ∞)
(b) (- ∞, – 1)
(c) (- ∞, ∞)
(d) (- 1, 1)

7. The minimum value of f (x) =|x + 2|is
(a) 2
(b) – 2
(c) 0
(d) None of these

8. An index number that can secure many purposes is called
(a) weighted index
(b) special purpose index
(c) general purpose index
(d) consumer price

9. To calculate Fisher’s price index, it uses
(a) only base year prices
(b) only current year and quantities
(c) current year, base year prices and quantities
(d) arithmetic mean

10. For given data, ∑p₁q₁ = 496, ∑p₀q₁ = 460, ∑p₀q₀ = 420 and ∑p₁q₀ = 480, where subscript 0 and 1 are used for base year and current year respectively. The Laspeyre’s price index is
(a) 110.43
(b) 114.29
(c) 115.34
(d) 113.43

11. Which of the following is the probability distribution of a random variable?

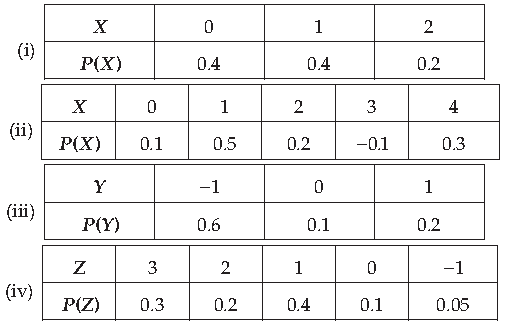
(a) Only (i)
(b) Only (ii)
(c) Both (iii) and (iv)
(d) None of these

12. If a die is thrown 5 times, then the probability that an odd number will come up exactly three times will be
(a) 3/16
(b) 4/16
(c) 5/16
(d) 6/16

13. Mean of a Poisson distribution is 6.25. Its variance is
(a) 3.75
(b) 6.25
(c) 4.75
(d) 5.75

14. 1000 light bulbs with a mean life of 120 days are installed in a new factory; their length of life is normally distributed with standard deviation 20 days. The number of bulbs will expire in less than 90 days are [given, F (1.5) = 0.9332]
(a) 63
(b) 64
(c) 67
(d) 668

15. In a 100 m race, A takes 36 s and B takes 45 s, then A defeat B with the distance of
(a) 20 m
(b) 25 m
(c) 50 m
(d) 15 m

16. The solution set of the inequality 2(2x + 3) – 10 < 6(x – 2) is
(a) x > 4
(b) x < 4
(c) x > 4
(d) x < 4

17. A and B entered into a partnership with capitals in the ratio 5 : 6. At the end of 8 months, A withdraws his capital. They received profits in the ratio 5 : 9. B invested capital for
(a) 6 months
(b) 8 months
(c) 10 months
(d) 12 months

18. The quantity of water must be added to 30L of milk at ` 60 per litre, so as to have mixture worth ` 50 per litre is
(a) 5L
(b) 6L
(c) 4L
(d) 10L

20. Aman can row upstream at 8 km/h and downstream at 13 km/h. The speed of the stream is
(a) 2.5 km/h
(b) 4.2 km/h
(c) 5 km/h
(d) None of these

Section B

21. The last two-digits of the product 4895 ₹ 6789 is
(a) 75
(b) 65
(c) 95
(d) 55

22. The non-negative remainder when 7 ³⁰ is divided by 5 is
(a) 4
(b) 3
(c) 2
(d) 1

(a) 0
(b) 1
(c) 2
(d) 3

(a) 60
(b) – 60
(c) 40
(d) – 40

25. If C(x) = ax² + bx + k is the total cost function, then slope of average cost curve is

26. The maximum profit that a company can make, if the profit function is given by P(x) = 41 + 24x – 18x² , is
(a) 49
(b) 47
(c) 45
(d) 43

27. The price and quantities of central commodities are shown in the following table

If ratio of Laspeyre’s (L) and Paasche’s (P) index number i.e. L : P = 15 :16, then the value of x is
(a) 1
(b) 4
(c) 3
(d) – 2

28. By using relative price, index number for the year 2018 with 2014 as base was 150, N = 5

(a) 30
(b) 35
(c) 42
(d) 40

29. For the given data ∑p₀ϖ = 7563 and ∑p₁ϖ = 8564, where subscript 0 and 1 are used for base year and current year respectively, then the index number is
(a) 110.85
(b) 113.24
(c) 121.22
(d) 124.19

30. Given that ∑p₀q₀ = 240, ∑p₁q₁ = 295, ∑p₀q₁ = 248 and ∑p₁q₀ = 252, where subscript 0 and 1 are used for base year and current year respectively. The Marshall-Edgeworth’s index number is
(a) 110.12
(b) 112.09
(c) 116.43
(d) 116.28

31. Given that, ∑p₀q₀ = 210, ∑p₁q₀ = 221, ∑p₀q₁ = 215 and ∑p₁q₁ = 232, where subscript 0 and 1 are used for base year and current year respectively. The Bowley’s price index number is
(a) 109.65
(b) 117.2
(c) 112.4
(d) 106.5

32. A company produces TV’s. The probability that any one TV is defective is 1/50 and they are packed in 10 big boxes. From a single big box, the probability that more than 8 TV’s work properly is

33. A coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, then in the probability distribution of number of tails, the maximum probability term is
(a) 3/8
(b) 1/16
(c) 9/16
(d) 10/16

34. For a Poisson’s distribution, 3P(X = 2) = P(X = 4). Find P(X = 3). (take e^-6 = 0.00248)
(a) 0.08928
(b) 0.09828
(c) 0.008928
(d) 0.009828

35. Assume the mean height of soldiers to be normally distributed with mean 68.22 inches and standard deviation of 10.8 inches. The number of soldiers in a regiment of 1000 would expect to be over six feet tall are [given, F (0.35) = 0.6368]
(a) 310
(b) 125
(c) 356
(d) 363

36. Three pipes A, B and C can fill a tank in 30 min, 20 min and 10 min, respectively. When the tank is empty, all the three pipes are opened. If A, B and C discharge chemical solutions P,Q and R respectively, then the part of solution R in the liquid in the tank after 3 min is
(a) 8/11
(b) 5/11
(c) 6/11
(d) 7/11

37. A, B, and C hire a meadow for ₹350. If they used it for 6 h, 10 h and 12 h respectively, then rent paid by C will be
(a) ₹ 75
(b) ₹ 125
(c) ₹ 150
(d) None of these

38. Aman can row at 16 km/h in still water and finds that it takes him thrice as much time to row up than as the row down the same distance in the river. The speed of the current is
(a) 10 km/h
(b) 12 km/h
(c) 8 km/h
(d) 6 km/h

39. The probability distribution of a random variable X is given as under

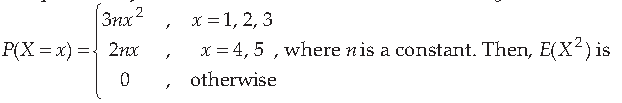
(a) 11.2
(b) 11.5
(c) 12.2
(d) 12.5

40. For the system of equations x + 2y – 3z = 6, 3x + 2y – 2z = 3 and 2x – y + z = 2, then the values of x, y and z are respectively
(a) 1, 5 and 5
(b) 1, – 5 and – 5
(c) 5, 1 and 5
(d) – 5, 1 and – 5

Section C

41. From a bag of 20 bulbs which includes 5 defectives, 2 bulbs are drawn one-by-one at random with replacement. Using the probability distribution of number of defective bulbs, the variance of the distribution is
(a) 1/8
(b) 1/4
(c) 3/8
(d) 1/2

42. In an examination 15% of the candidates got first class (60% marks or above) while 40% failed (securing below 40%). Assuming the marks to be normally distributed, the mean and standard deviation are
(a) 41.35 and 13.5
(b) 41.35 and 13.7
(c) 43.87 and 15.5
(d) 43.87 and 13.5

43. The interval in which f (x) = x ⁴ – 2x² is increasing is
(a) (- 1, 0)
(b) (1, ∞)
(c) (0, 1)
(d) (- 1, 0)Ù(1, ∞)

44. If a tap A is 5 times faster than tap B and can fill a tank in 32 min less than tap B, then the time taken to fill the tank if both pipes are opened together is

45. The value of x for which the f(x) = x + (1/x) is increasing, is
(a) (- ∞,1)
(b) (- ∞,0)
(c) (1, ∞)
(d) (0, ∞)

Case Study
The inter-industry flow of the products of two industries is given as under

On the basis of above information answer the following questions for the final demands of 36 and 88 units respectively

46. The technology matrix A is

47. The demand matrix D is

48. (I – A) is

49. (I – A)^-1 is

50. The gross output of two industries I and II are respectively.
(a) 160 units and 200 units
(b) 160 units and 240 units
(c) 240 units and 160 units
(d) None of these