Class 12 Mathematics Sample Paper Set M
Please see below Class 12 Mathematics Sample Paper Set M with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.
CBSE Sample Paper for Class 12 Mathematics Set M
1. Let the equations of two sides of a triangle be 3x – 2y + 6 = 0 and 4x + 5y – 20 = 0. If the orthocentre of this triangle is at (1, 1) then the equation of its third side is
(a) 122y – 26x – 1675 = 0
(b) 26x – 122y – 1675 = 0
(c) 122y + 26x + 1675 = 0
(d) 26x + 61y + 1675 = 0
Answer
B
2. Let z0 be a root of the quadratic equation, x2 + x+ 1 = 0, If z = 3 + 6iz081-3izo93, then arg z is equal to
(a) π/4
(b) π/6
(c) 0
(d) π/3
Answer
A
3.
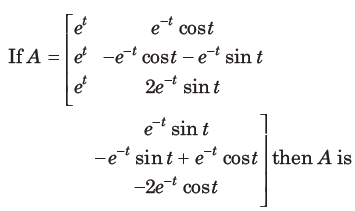
(a) invertible only when t = π
(b) invertible for every t ∈ R
(c) not invertible for any t ∈ R
(d) invertible only when t = π/2
Answer
B
4. A pot contain 5 red and 2 green balls.
At random a ball is drawn from this pot. If a drawn ball is green then put a red ball in the pot and if a drawn ball is red, then put a green ball in the pot, while drawn ball is not replace in the pot. Now we draw another ball randomnly, the probability of second ball to be red is
(a)27/49
(b)26/49
(c)21/49
(d)32/49
Answer
D
5. Let f be a differentiable function from R to R such that
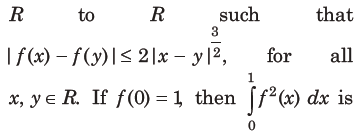
equal to
(a) 2
(b)1/2
(c) 1
(d) 0
Answer
C
6. If lines x = ay + b, z = cy + d and x = a’z + b’, y = c’z + d’ are perpendicular, then
(a) ab’+ bc’+1 = 0
(b) bb’+ cc’+1 = 0
(c) aa’+ c + c’= 0
(d) cc’+ a + a’= 0
Answer
C
7. The area of the region
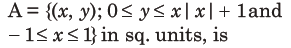
(a) 2
(b)4/3
(c)1/3
(d)2/3
Answer
A
8. The equation of the plane containing the straight line x/2=y/3=z/4 = and perpendicular to the plane containing the straight lines x/3= y/4= z/2 and x/4=y/2=z/3 is
(a) 5x + 2y – 4z = 0
(b) x + 2y – 2z = 0
(c) 3x + 2y – 3z = 0
(d) x – 2y + z = 0
Answer
D
9.
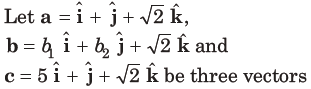
such that the projection vector of b on a is a. If a + b is perpendicular to c, then|b|is equal to
(a) 6
(b) 4
(c) 22
(d) 32
Answer
A
10. If x = sin-1 (sin 10) and y = cos-1 (cos 10) , then y – x is equal to
(a) 0
(b) 10
(c) 7π
(d) π
Answer
D
11. Let a, b and c be the 7th, 11th and 13th terms respectively of a non-constant AP. If these are also the three consecutive terms of a GP, then a/c is equal to
(a) 2
(b)7/13
(c) 4
(d)1/2
Answer
C
12. Let A = { x ∈R : x is not a positive integer}. Define a function f : A → R as f (x)=2x/x-1, then f is
(a) injective but not surjective
(b) not injective
(c) surjective but not injective
(d) neither injective nor surjective
Answer
A
13. In a group of data, there are n observations, x, x2,….xn. If
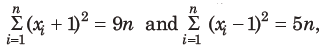
the standard deviation of the data is
(a) 2
(b) √7
(c) 5
(d) √5
Answer
D
14. If 0≤x<π/2, then the number of values of x for which sin x – sin 2x + sin 3x = 0, is
(a) 2
(b) 3
(c) 1
(d) 4
Answer
A
15. If the system of linear equations
x – 4y + 7z = g
3y – 5z = h
– 2x + 5y – 9z = k
is consistent, then
(a) 2g + h + k = 0
(b) g + 2h + k = 0
(c) g + h + k = 0
(d) g + h + 2k = 0
Answer
A
16. Let A (4, – 4) and B(9, 6) be points on the parabola, y2= 4x Let C be chosen on the arc AOB of the parabola, where O is the origin, such that the area of Δ ACB is maximum. Then, the area (in sq. units) of Δ ACB, is
(a) 311/4
(b) 32
(c) 313/4
(d) 301/2
Answer
A
17. The number of all possible positive integral values of a for which the roots of the quadratic equation,6x2-11x+α = 0 are rational numbers is
(a) 5
(b) 2
(c) 4
(d) 3
Answer
D
18. For each x ∈ R, let [x]be the greatest integer less than or equal to x. Then,
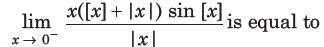
(a) 0
(b) sin 1
(c) – sin 1
(d) 1
Answer
C
19. The coefficient of t4 in the expansion of
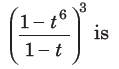
(a) 12
(b) 10
(c) 15
(d) 14
Answer
C
20. Let S be the set of all triangles in the xy-plane, each having one vertex at the origin and the other two vertices lie on coordinate axes with integral coordinates. If each triangle in S has area 50 sq. units, then the number of elements in the set S is
(a) 36
(b) 32
(c) 18
(d) 9
Answer
A
21. The logical statement
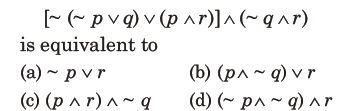
Answer
C
22. If the circles x2+y2-16x-20y+164=r2 and (x – 4)2 + (y – 7)2 = 36 intersect at two distinct points, then
(a) 0 < r < 1
(b) r > 11
(c) 1 < r < 11
(d) r = 11
Answer
C
23. If both the roots of the quadratic equation x2-mx+4=0 are real and distinct and they lie in the interval [1, 5] then m lies in the interval
(a) (4, 5)
(b) (-5, – 4)
(c) (5, 6)
(d) (3, 4)
Answer
A
24. The number of natural numbers less than 7,000 which can be formed by using the digits 0, 1, 3, 7, 9 (repitition of digits allowed) is equal to
(a) 374
(b) 375
(c) 372
(d) 250
Answer
A
25.
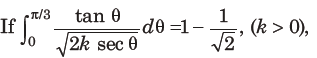
then the value of k is
(a) 1
(b)1/2
(c) 2
(d) 4
Answer
C
26.
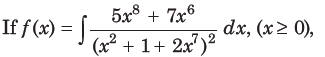
and f (0) = 0, then the value of f (1) is
(a) – 1/2
(b) – 1/4
(c)1/4
(d)1/2
Answer
C
27. Let f : [0, 1]→ R be such that f (xy) = f (x). f (y), for all x, y ∈[0, 1]and f (0) ≠ 0. If y = y (x) satisfies the differential equation,dy/dx= f (x) with y(0) = 1, then y(1/4) +y (3/4)is equal to
(a) 5
(b) 3
(c) 2
(d) 4
Answer
B
28. The sum of the following series
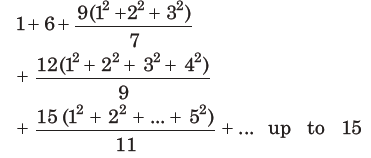
terms is
(a) 7510
(b) 7820
(c) 7830
(d) 7520
Answer
B
29. If x = 3 tan t and y = 3 sec t, then the value of d2 y/dx2 at t = π/4, is
(a)1/6
(b)16/√2
(c)13√2
(d)3/2√2
Answer
B
30. A hyperbola has its centre at the origin, passes through the point (4, 2) and has transverse axis of length 4 along the X-axis. Then the eccentricity of the hyperbola is
(a) 2
(b)2/√3
(c)3/2
(d) √3
Answer
B
