Class 12 Mathematics Sample Paper Set L
Please see below Class 12 Mathematics Sample Paper Set L with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.
CBSE Sample Paper for Class 12 Mathematics Set L
1.then x is equal to
(a)√145/10
(b)√146/12
(c)√145/12
(d)√145.11
Answer
C
2. The value of
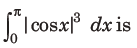
(a)2/3
(b) – 4/3
(c) 0
(d)4/3
Answer
D
3.
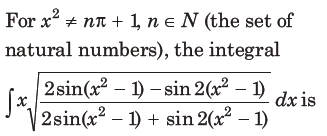
equal to (where C is a constant of integration)
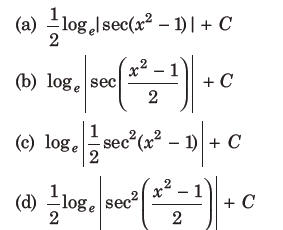
Answer
B
4. If y = y(x) is the solution of the differential equation, x dy/dx+2y=x2 satisfying y(1) =1, then y(1/2)is equal to
(a)13/16
(b)1/4
(c)49/16
(d)7/64
Answer
C
5. The equation of the line passing through (-4, 3, 1), parallel to the plane x + 2y – z – 5 = 0 and intersecting the line
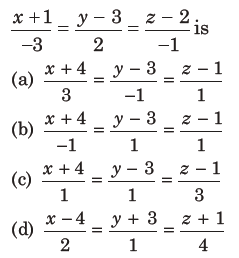
Answer
A
6 Let f :R→ R be a function defined as
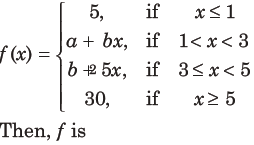
(a) continuous if a = – 5 and b = 10
(b) continuous if a = 5 and b = 5
(c) continuous if a = 0 and b = 5
(d) not continuous for any values of a and b
Answer
D
7. Axis of a parabola lies along X-axis. If its vertex and focus are at distances 2 and 4 respectively from the origin, on the positive X-axis, then which of the following points does not lie on it?
(a) (4, -4)
(b) (6, 4 2)
(c) (8, 6)
(d) (5, 2 6)
Answer
C
8. Consider the set of all lines px + qy + r = 0 such that 3p + 2q + 4r = 0. Which one of the following statements is true?
(a) Each line passes through the origin.
(b) The lines are concurrent at the point (3/4,1/2)
(c) The lines are all parallel
(d) The lines are not concurrent
Answer
B
9. Let α and β be two roots of the equation x2+2x+2=0, then α15 + β15 is equal to
(a) 256
(b) 512
(c) -256
(d) -512
Answer
C
10. If the fractional part of the number 2403/15 is k/15,, then k is equal to
(a) 14
(b) 6
(c) 4
(d) 8
Answer
D
11. 5 students of a class have an average height 150 cm and variance 18 cm2. A new student, whose height is 156 cm, joined them. The variance (in cm 2 ) of the height of these six students is
(a) 16
(b) 22
(c) 20
(d) 18
Answer
C
12. If a, b and c be three distinct real numbers in GP and a + b + c = xb, then x cannot be
(a) 4
(b) 2
(c) -2
(d) -3
Answer
B
13. The plane through the intersection of the planes x + y + z = 1and 2x + 3y – z + 4 = 0 and parallel to Y-axis also passes through the point
(a) (3, 3; -1)
(b) (-3, 1, 1)
(c) (3, 2, 1)
(d) (-3, 0, -1)
Answer
C
14 The maximum volume (in cu.m) of the right circular cone having slant height 3m is
(a)4/3π
(b) 2√3π
(c) 3√3π
(d) 6π
Answer
C
15.
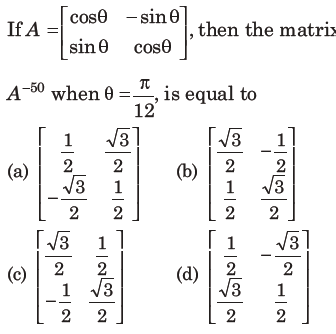
Answer
C
16. For x ∈ R – {0, 1}, let f1(x)=1/x,f2(x)=1-x and f3 (x),then j(x),is equal to
(a) f2 (x)
(b) f3 (x)
(c) f1(x)
(d)1/xf3 (x)
Answer
B
17. Consider a class of 5 girls and 7 boys.
The number of different teams consisting of 2 girls and 3 boys that can be formed from this class, if there are two specific boys A and B, who refuse to be the members of the same team, is
(a) 350
(b) 500
(c) 200
(d) 300
Answer
D
19. Three circles of radii a, b,c(a < b < c) touch each other externally. If they have X-axis as a common tangent, then
(a) a, b, c are in AP
(b)1/√a=1/√b+1/√c
(c) √a , √b, √c are in AP
(d)1/√b= 1/√a+ 1/√c
Answer
B
20. For any θ∈ (π/4,π/2),, , the expression 3 (sinθ – cosθ)4 +6 (sinθ + cosθ)2+4sin6θ equals
(a) 13 – 4 cos4 θ + 2sin2θ cos⊕2θ
(b) 13 – cos2θ+ 6cos4 θ
(c) 13- 4cos2θ + sin2θcos2θ
(d) 13 4 – cos6θ
Answer
D
21. If the Boolean expression (p⊕q)∧(~ p· q) is equivalent to p∧ q, where ⊕,· ∈{∧,v}, then the ordered pair(⊕,·×) is
(a) (∧, v)
(b) (∧, ∧)
(c) (v, ∧)
(d) (v, v)
Answer
A
22. Equation of a common tangent to the circle, x2+y2-6x=0 and the parabola, y2=4x , is
(a) √3y = 3x + 1
(b) 2√3y = 12x + 1
(c) √3y = x + 3
(d) 2√3y = – x – 12
Answer
C
23.
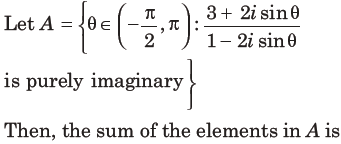
(a)3π/4
(b)5π/6
(c) π
(d)2π/3
Answer
D
25. The system of linear equations
x + y + z = 2
2x + 3y + 2z = 5
2x +3y+(a2-1)z=a+1
(a) has infinitely many solutions for a = 4
(b) is inconsistent when a = 4
(c) has a unique solution for|a|= √3
(d) is inconsistent when|a|= √3
Answer
D
26. The area (in sq units) bounded by the parabola y = x2 – 1, the tangent at the point (2, 3) to it and the Y-axis is
(a)8/3
(b)56/3
(c)32/3
(d)14/3
Answer
A
27.
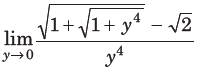
(a) exists and equals 1/4√2
(b) does not exist
(c) exists and equals 1/2√2
(d) exists and equals 1/2√2(√2+1)
Answer
A
28. Let 0<θ<π/2. If the eccentricity of the hyperbola x2/cos2θ- y2/sin2θ = 1 is greater than 2, then the length of its latus rectum lies in the interval
(a) (1,3/2-]
(b) (3,∞)
(c) (3/2,2]
(d) (2, 3]
Answer
B
29.
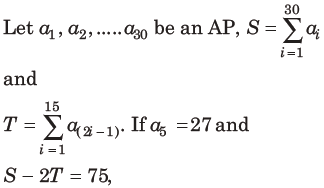
then a10 is equal to
(a) 42
(b) 57
(c) 52
(d) 47
Answer
C
30. Two cards are drawn successively with replacement from a well shuffled deck of 52 cards. Let X denote the random variable of number of aces obtained in the two drawn cards.
Then, P(X = 1) + P(X = 2) equals
(a)25/169
(b)52/169
(c)49/169
(d)24/169
Answer
A
