Please see below Class 12 Mathematics Sample Paper Set A with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.

CBSE Sample Paper for Class 12 Mathematics Set A

PART – A
Section – I

1. Find x and y such that

Answer : 

⇒ x – y = 5 …(i)
and 2x – y =12 …(ii)
Subtracting (i) from (ii), we get x = 7
From (i), y = x – 5 = 7 – 5 = 2

OR

For what value of x, the matrix

 is a skew-symmetric matrix?
Answer : 

2. PO + OQ = QO + OR show that the points P, Q, R are collinear.
Answer : 

3. Evaluate : ∫sin3x cos3x dx
Answer : 

OR

Evaluate : 

Answer : 

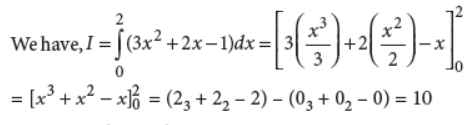
4. If (1/2,1/3n) are the direction cosines of a line, then find the value of n.
Answer : 

5. Show that the function f : N → N given by f(x) = 4x, is one-one but not onto.
Answer : For one-one : Consider, f(x1) = f(x2)
⇒ 4x₁ = 4x₂ ⇒ x₁ = x₂
Hence, f is one-one.
For onto : Let y be any element in N(co-domain), then
f(x) = y ⇒ 4x = y

OR

Let f : R → R be a function defined by f(x) = x3 + 4, then check whether f is a bijection or not.
Answer : 

6. If 

 is a singular matrix, then find the value of x.
Answer : Since the given matrix is singular.

⇒ (2 + x)(5 – 2) –3(–5 – 2x) + 4(1 + x) = 0
⇒ 13x = –25 ⇒ x = −25/13

7. Find the distance of the plane 3x – 6y + 2z + 11 = 0 from the origin.
Answer : We have, equation of plane is 3x – 6y + 2z + 11 = 0.
Its distance from origin (0, 0, 0) is

OR

Find the value of l such that the lines x/1 = y/3 = z/2λ and x/-3 = y/5 = z/2 are perpendicular to each other.
Answer : Direction ratios of the given lines are (λ, 3, 2l) and (–3,
5, 2) respectively. Since, the lines are at right angles, so
(λ) × (–3) + (3) × (5) + 2(2l) = 0
⇒ –3 + λ5 + 4l = 0 ⇒ λ = –3

8. If 

 then find AT – BT.
Answer : Given,

9. Let A and B be independent events with P(A) = 1/4 and P(A ∪ B) = 2P(B) – P(A). Find P(B).
Answer : We have, P(A) = 1/4
Now, P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= P(A) + P(B) – P(A) P(B) ( ∵ A, B are independent)
⇒ 1/4 + P(B) – (1/4) P(B) = 2P(B) – 1/4 (Given)
⇒ P(B) = 2/5

OR

A and B are events such that P(A) = 0.4, P(B) = 0.3 and P(A ∪ B) = 0.5. Then find P(B′ ∩ A).
Answer : Given, P(A) = 0.4, P(B) = 0.3 and P(A ∪ B) = 0.5.
Clearly, P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= 0.4 + 0.3 – 0.5 = 0.2
Now, P(B′ ∩ A) = P(A) – P(A ∩ B) = 0.4 – 0.2 = 0.2 = 1/5

10. Let R = {(3, 1), (1, 3), (3, 3)} be a relation defined on the set A = {1, 2, 3}. check whether R is symmetric, transitive or reflexive.
Answer : Given that, R = {(3, 1), (1, 3), (3, 3)} be defined on the set A = {1, 2, 3}.
Q (2, 2) ∉ R. Therefore, R is not reflexive.
Q (3, 1) ∈ R, (1, 3) ∈ R. Hence, R is symmetric.
Since, (1, 3) ∈ R, (3, 1) ∈ R but (1, 1) ∉ R
So, R is not transitive.

11. The position vectors of points A, B, C, D are ā, Ђ , 2ā +3Ђ and ā -2Ђ respectively. Find DB and AC.
Answer : 

12. Evaluate : 

Answer :

13. If P(A) = 7/13, P(B) =9/13 and P(A∩B) = 4/13 ,then find the value of P(A | B).
Answer : 

14. Find the order and degree for the differential equation x dy/dx + 2y =xy dy/dx.
Answer : Given, (1 − y)x dy/dx + 2y = 0
Order and degree for the above equation are 1 and 1 respectively.

15. Find the equation of a line passing through a point (2, –1, 3) and parallel to the line r̄ = (î +ĵ ) +λ (2î +ĵ −2k̂).
Answer : The given line is parallel to the vector 2î +ĵ −2k̂ and the required line is parallel to the given line. So, required line is parallel to the vector 2î +ĵ −2k̂ Thus, the equation of the required line passing through (2, –1, 3) is
r̄ = (2î +ĵ −2k̂) +μ (2î +ĵ −2k̂)

16. Find the number of equivalence relations on the set {1, 2, 3} containing (1, 3) and (3, 1).
Answer : Equivalence relations on the set {1, 2, 3} containing (1, 3) and (3, 1) are
A1 = {(1, 1), (2, 2), (3, 3), (1, 3), (3, 1)}
A2 = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (2, 3), (3, 1), (3, 2), (1, 3)}
So, only two equivalence relations exist.

Section – II

Case study-based questions are compulsory. Attempt any 4 sub parts from each question. Each sub-part carries 1 mark.

17. An owner of a car rental company have determined that if they charge customers ₹ x per day to rent a car, where 50 ≤ x ≤ 200, then number of cars (n), they rent per day can be shown by linear function n(x) = 1000 – 5x. If they charge ₹ 50 per day or less they will rent all their cars. If they charge ₹ 200 or more per day they will not rent any car. 

Based on the above information, answer the following question.
(i) Total revenue R as a function of x can be represented as
(a) 1000x – 5×2
(b) 1000x + 5×2
(c) 1000 – 5x
(d) 1000 – 5×2
Answer : A

(ii) If R(x) denote the revenue, then maximum value of R(x) occur when x equals
(a) 10
(b) 100
(c) 1000
(d) 50
Answer : B

(iii) At x = 220, the revenue collected by the company is
(a) ₹ 10
(b) ₹ 500
(c) ₹ 0
(d) ₹ 1000
Answer : C

(iv) The number of cars rented per day, if x = 75 is
(a) 675
(b) 700
(c) 625
(d) 600
Answer : C

(v) Maximum revenue collected by company is
(a) ₹ 40000
(b) ₹ 45000
(c) ₹ 55000
(d) ₹ 50000
Answer : D

18. In a family, on the occasion of Diwali celebration father, mother, daughter and son line up at random for a family photograph.
(i) Find the probability that son is at one end, given that father and mother are in the middle.
(a) 1
(b) 1/2
(c) 1/3
(d) 2/3
Answer : A

(ii) Find the probability that mother is at left end, given that son and daughter are together.
(a) 1/2
(b) 1/3
(c) 1/4
(d) 0
Answer : B

(iii) Find the probability that father and mother are in the middle, given that daughter is at right end.
(a) 1/4
(b) 1/2
(c) 1/3
(d) 2/3
Answer : C

(iv) Find the probability that mother and son are standing together, given that father and daughter are standing together.
(a) 0
(b) 1
(c) 1/2
(d) 2/3
Answer : D

(v) Find the probability that father and mother are on either of the ends, given that daughter is at second position from right end.
(a) 1/3
(b) 2/3
(c) 1/4
(d) 2/5
Answer : A

PART – B
Section – III

19. Find the value of the constant k so that the function f, defined below, is continuous at x = 0.

Answer : 

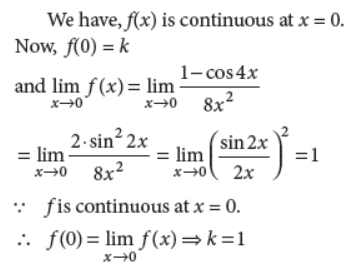
20. Evaluate :

Answer : 

OR

Evaluate : ∫| x |dx
Answer : 

21. If 0 < x < 1, then √(1+x2) [(x cos[cot-1 x]+ sin[cot-1 x])2-1]1/2
Answer : 

22. Show that the function f given by f(x) = x³ – 3x² + 4x, x ∈R is increasing on R. .
Answer : Here f(x) = x³ – 3x² + 4x
⇒ f ′(x) = 3x² – 6x + 4 = 3(x² – 2x) + 4
= 3(x² – 2x + 1) – 3 + 4
= 3(x – 1)² + 1 > 0 ∀x ∈R
⇒ f is increasing on R.

23. If ā=î+ĵ+2 k̂ and Ђ= 3î+2 ĵ − k̂ , then find (ā+3Ђ).(2ā-Ђ)
Answer : Here ā+3Ђ = î + ĵ + 2k̂+3(3î + 2ĵ −2k̂)
= 10î + 7ĵ − k̂
and 2ā−3Ђ =( î + ĵ + 2)k̂−(3î + 2ĵ −k̂)
= −î + 5k
and ∴ (ā+3Ђ) .(2ā−Ђ) = (10î + 7ĵ −k̂) .(î + 5k̂)
= 10 × (–1) + 7 × 0 + (–1) × 5 = –15

OR

ā=î+ĵ+k̂, Ђ= î+ĵ , ċ=î and (ā ×Ђ)×ċ = λa +μЂ, then find the value of λ + μ.
Answer : 

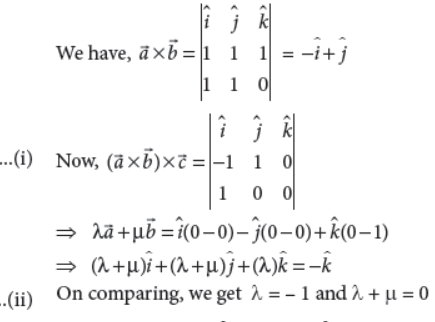
24. Find the area bounded by the curve x = 3y² – 9 and the line x = 0, y = 0 and y = 1.
Answer : We have, x = 3y² – 9 ⇒ 3y² = x + 9

Required area = area of shaded region

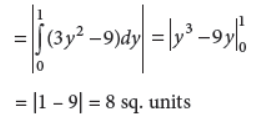
25. Two cards are drawn successively, without replacement, from a well-shuffled pack of 52 cards. Find the probability distribution of number of spades.
Answer : Let the random variable X be defined as the number of spades in a draw of 2 cards successively without replacement, then X can take values 0, 1, 2.
P(X = 0) = P(drawing no spade cards)

26. Differentiate (tan^-1 x^1/3 + tan^-1a^1/3 )
Answer : Let y = tan^–1x1/3 + tan^–1a1/3
Differentiating w.r.t. x, we get

27. Given

Answer : We have,

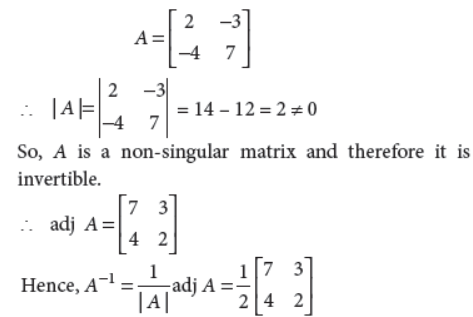
28. If l₁, m₁, n₁ and l₂, m₂, n₂ be the direction cosines of two lines, show that the direction cosines of the line perpendicular to both of them are proportional to (m₁n₂ – m₂n₁), (n₁l₂ – n₂l₁), (l₁m₂ – l₂m₁).
Answer : Let l, m, n be the direction cosines of the line perpendicular to each of the given lines. Then,
ll₁ + mm₁ + nn₁ = 0 …(i)
and ll₂ + mm₂ + nn₂ = 0 …(ii)
On solving (i) and (ii), we get

Hence, the direction cosines of the line perpendicular to the given lines are proportional to (m₁n₂ – m₂n₁),
(n₁l₂ – n₂l₁), (l₁m₂ – l₂m₁).

OR

Find the equation of a line passing through the point (– 3, 2, –4) and equally inclined to the axes.
Answer : Since, the line is equally inclined to the axes.

Section – IV

29. Determine the value of the constant k so that the function 

Answer : We have, L.H.L. (at x = 0)

30. Find the area of the region bounded by the lines y = |x – 3| and the lines x = 2, x = 4 and x-axis.
Answer : We have,

31. Let A = R –{3}, B = R –{1} and f : A → B be defined by f (x) = x-2/x-3 Then, prove that f is bijective.
Answer : Let x and y be two arbitrary elements in A.

Thus, every element in the co-domain B has its pre-image in A, so f is a surjective. Hence, f : A → B is
bijective.

OR

Let A = {x : –1 ≤ x ≤ 1} and f : A → A is a function defined by f(x) = x |x|, then check whether f is a bijection or not.
Answer : 

The graph shows f(x) is one-one, as any straight line parallel to x-axis cuts only at one point. Here, range of f(x) ∈ [–1, 1]. Thus range = co-domain. Hence, f(x) is onto. Therefore f(x) is one-one and onto, i.e, bijective.

32. A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening.
Answer : Let dimensions of the rectangle be x and y (as shown).
∴ Perimeter of window,

33. If 

(where C is a constant of integration), then find the value of ordered pair (K, A).
Answer : We have,

OR

34. Find the solution of the differential equation y² dx + (xy + x²) dy = 0.
Answer : 

or

Find the particular solution of ln , (dy/dx) = 3x + 4y , (y)0 =0.
Answer : 

35. Show that f(x) = | x – 3 |, ∀ x ∈R is continuous but not differentiable at x = 3.
Answer : 

Thus, Lf ′(3) ≠ Rf ′(3)
Hence, f(x) is not differentiable at x = 3.

36. Minimize z = x+2y, subject to x+2y ≥ 50, 2x–y ≤ 0, 2x+y ≤ 100, x, y ≥ 0.
Answer : First we draw the lines whose equations are
x + 2y = 50, 2x – y = 0 and 2x + y = 100 respectively.

The feasible region is BCPDB which is shaded in the figure.
The vertices of the feasible region are B(0, 25), C(10, 20), P(25, 50) and D(0, 100).
The values of the objective function z = x + 2y at these vertices are given below.

Corner points	Value of z = x + 2y
B(0, 25) C(10, 20) P(25, 50) D(0, 100)	50 (minimum) 50 (minimum) 125 200

∴ z has minimum value 50 at two consecutive vertices B and C.
∴ z has minimum value 50 at every point of segment joining the points B(0, 25) and C(10, 20).
Hence, there are infinite number of optimal solutions.

OR

Find the maximum value of z = 11x+8y subject to x≤ 4, y≤6, x+y≤6, x≥0, y≥0.
Answer : Convert the inequations into equations and draw the corresponding lines.
x + y = 6, x = 4, y = 6
As x, y ≥ 0, the solution lies in the first quadrant.

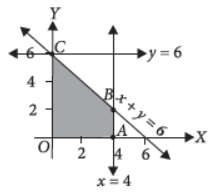
We have seen that O, A, B, C are the corner points.
Hence maximum value of the objective function z will occur at one of the corner points.
B is the point of intersection of the lines x + y = 6 and x = 4 i.e., B (4, 2)
We have points A(4, 0), B(4, 2) and C(0, 6)
Now, z = 11x + 8y
∴ z(A) = 11(4) + 8(0) = 44
z(B) = 11(4) + 8(2) = 60
z(C) = 11(0) + 8(6) = 48
z(O) = 11(0) + 8(0) = 0
∴ z has maximum value 60 at B(4, 2).

37. If A

Answer : 

OR

Find the inverse of the matrix

 by using adjoint method, if it exists. Also, find (adj A)².
Answer : 

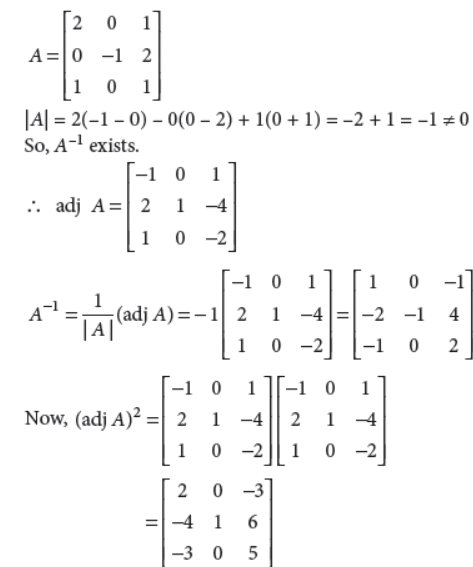
38. Find the equation of the plane passing through the point 2î-k̂ and parallel to the lines 

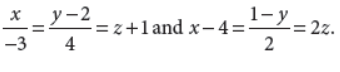
Answer : The required plane passes through the point with position vector

i.e. parallel to the lines whose direction ratios are

OR

A perpendicular is drawn from the point P(2, 4, –1) to the line x+5/1 = y+3/4 = z-6/-9 Find the equation of the perpendicular from P to the given line.
Answer : Let M be the foot of the perpendicular drawn from the point P(2, 4, –1) to the given line.
The coordinates of any point on the line

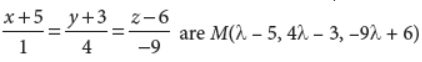
Direction ratios of PM are
λ – 7, 4λ – 7, –9λ + 7
The direction ratios of the given line are 1, 4, –9
Since PM is perpendicular to the given line.
∴ 1(λ– 7) + 4(4λ – 7) – 9(–9λ + 7) = 0
⇒ 98l – 98 = 0 ⇒ l = 1
Putting λ = 1, we have
M ≡ (–4, 1, –3)
Now, equation of PM = equation of the perpendicular
from P to the given line