Please see below Class 12 Mathematics Sample Paper Term 1 Set B with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Term 1 Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.

CBSE Sample Paper for Class 12 Mathematics Term 1 Set B

SECTION-A

In this section, attempt any 16 questions out of Questions 1 –20.
Each Question is of 1 mark weightage.

1. The domain of function cos–1(2x – 1) is:
(A) [0, 1]
(B) [–1, 1)
(C) (–1, 1)
(D) [0, π]

2. Find dy/dx where x = sin q and y = cos θ.
(A) cot θ
(B) tan θ
(C) –cot θ
(D) –tan θ

3. The value of the determinant

(A) 250
(B) –260
(C) –250
(D) 0

4. If matrix A = [9 10 11]. Write AA’ where A’ is the transpose of matrix A.
(A) 304
(B) 301
(C) 300
(D) 302

5. If y = 7x – x³ and x increase at the rate of 4 units per second, how fast is the slope of the curve changing when x = 2 ?
(A) –48
(B) –46
(C) –40
(D) –56

6. For the given matrix, the value of y is

(A) y = 3
(B) y = 14
(C) y = 21
(D) y = –20

7. Set A has 5 elements and set B has 6 elements. Then the number of injective mappings that can be defined from A to B is
(A) 744
(B) 712
(C) 724
(D) 720

8. If the matrix A =

is singular, then the value of x is:
(A) 1
(B) –2
(C) 2
(D) –1

9. If the function f(x) =

is continuous at x = 3, then the value of k is:
(A) 7
(B) 6
(C) 8
(D) 10

10. If a relation R on the set {4, 5, 6} be defined by R = {(5, 5)}, then R is
(A) reflexive
(B) transitive
(C) symmetric
(D) None of these

11. The principal value branch of cosec–1x is:
(A) (-π/2, π/2)
(B) [0, π] – { π/2}
(C) (π/2, -π/2)
(D) [-π/2, -π/2] – {0}

12. The derivative of log tan (π/4 + x/2) is:
(A) sin x
(B) sec x
(C) cosec x
(D) cot x

13. Consider a square matrix A =

. The given matrix is an example of
(A) Diagonal matrix
(B) Identity matrix
(C) Scalar matrix
(D) Null matrix

14. If y = x + logx³ then the value of dy/dx is
(A) 1 + 3/x
(B) 1 + 3/x²
(C) 1 + log x
(D) 3/x

15. If A =

then A² – 6A + 17I is:

16. The equation of the tangent to the curve y = –4x² + 9x + 17 at the point (1, 2) is:
(A) x – y = –10
(B) y – x = 1
(C) x + y = 1
(D) x – y = 10

17. The value of x for the given determinant

(A) -1/5
(B) -1/4
(C) 1/4
(D) -1/5

18. The equation of normal to the curve y = 10x² – 9 sin x at x = 0 is:
(A) y – 9x = 0
(B) x = –9y
(C) x – 9y = 0
(D) y – 9x = 0

19. Corner points of feasible region for an LPP are (0, 0), (2, 0), (2 ,1/2) , (0, 2). Let Z = 60x + 80y be the objective function. The maximum value of Z is:
(A) 140
(B) 120
(C) 130
(D) 160

20. The interval for which f(x) = x⁴ – 2x² is increasing on:
(A) (–∞, –1) ∪ (0, 1)
(B) (∞, 1) ∪ (0, –1)
(C) (–1, 0) ∪ (1, ∞)
(D) (1, 0) ∪ (1, –∞)

SECTION-B

In this section, attempt any 16 questions out of the Questions 21 -40.
Each Question is of 1 mark weightage.

21. It is the domain of the function f(x) = – √-5 – 6x – x²
(A) [–5, –1]
(B) [–2, 3]
(C) [1, –5]
(D) [–6, –1]

22. What is the derivative of sin²(x³) w.r.t. x:
(A) xsin x³.cos x³
(B) 2xsinx³.cosx³
(C) 6x²sinx³.cosx³
(D) 6xsinx³.cosx³

23. Corner points of the feasible region for an LPP are (0, 2), (4, 0), (0, 4). Let Z = 3x + 4y be the objective function. The minimum value of Z occurs at
(A) at (0, 0)
(B) at (4, 0)
(C) at (0, 4)
(D) mid point of (0, 0) and (4, 0)

24. Consider the curve y = x²/4 . The Slope of the line parallel to tangent to the curve at x = 2 is
(A) 1/4
(B) -1/2
(C) 1/3
(D) 1

25. If

then the value of y is
(A) 3
(B) ±6
(C) -1/4
(D) -2/3

26. Given a function f (x)= 2x³ −21x² +60x ,+ it4 h8as local maximum at x =
(A) 3
(B) 6
(C) 2
(D) 5

27. What is the principal value of sin-1(-√3/2) ?
(A) π/3
(B) -π/3
(C) π/2
(D) π/6

28. For what value of x, the matrix

is singular?
(A) 4
(B) 6
(C) 3
(D) 1

29. If y = tan -1(3x-x³/1-3x²) , 1/√3 < x < 1/√3 dy/dx will be
(A) 3/1+x²
(B) 2/1+x²
(C) 3/3+x²
(D) 2/3+x²

30. Let f : R → R be a function such that f(x) = 2x. What is the range of f ?
(A) (–∞, 0]
(B) [0, ∞)
(C) R–
(D) R+

31. What is the derivative of sin–1x ?
(A) 1/√1-x²
(B) -1/√1-x²
(C) 1/1+x²
(D) 1/x√x² – 1

32. If [a 1]

= 0, then a will be:
(A) –2
(B) 2
(C) 0
(D) 1

33. In LPP if (4, 0), (0, 0), (4, 4) and (0, 4) are the corner points of feasible region and Z = 3x + 4y Then Z will be maximum at point:
(A) (4, 0)
(B) (0, 0)
(C) (4, 4)
(D) (0, 4)

34. Find the local maxima and local minima of f(x) = 1/x²+2 .
(A) x = 1
(B) x = 0
(C) x = 2
(D) x = 6

35. If A = [2 –3 4], B =

(A) [8]
(B) [6]
(C) [2]
(D) [9]

36. The Given relation R = {(a, b) : a = b} is:
(A) symmetric relation
(B) transitive relation
(C) equivalence relation
(D) reflexive relation

37. What is the domain of f(x) = x³ – x² + 4x +7/3x + 11
(A) R – {-11/3}
(B) R
(C) R – {0}
(D) R – {11/3}

38. If

then what is the value of R.
(A) 6
(B) 17
(C) 15
(D) 10

39. The equation of tangent to the curve y(1 + x²) = 3 – x where it croses x-axis is:
(A) x + 3y = 9
(B) x + 6y = 2
(C) x – 10y = 3
(D) x + 10y = 3

40. If

, then what is the value of x ?
(A) 3
(B) 2
(C) 5
(D) 8

SECTION-C

In this section, attempt any 8 questions. Each question is of 1-mark weightage.
Questions 46-50 are based on a Case-Study.

41. The objective function is Z = 5x + 3y and the corner points are (0, 0), (2, 0), (0, 3) and (20/19 , 45/19) then Z is maximum at:
(A) (2, 0)
(B) (0, 0)
(C) (20/19 , 45/19)
(D) (0, 3)

42. If y = x² + ax + b has a minimum at x = 3, then what is the value of a
(A) –6
(B) 3
(C) –2
(D) 1

43. What is the least value of the function f(x) = cos–1x² in the interval [-1/√2 , 1/√2] ?
(A) π/6
(B) π/3
(C) π/4
(D) π/4

44. From the figure which point is not the corner point of feasible region

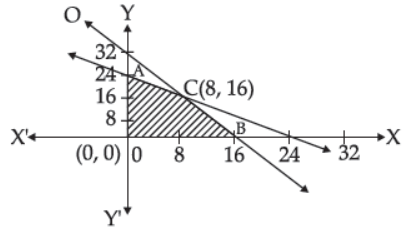
(A) (0, 24)
(B) (8, 16)
(C) (16, 0)
(D) (16, 16)

45. If A =

then what is the value of A – B.

CASE-STUDY

In the school project Sheetal was asked to construct a triangle and name it as ABC. Two angles A and B were given to be equal to tan-1 1/2 and tan-1 1/3 respectively.

46. The value of sin A is _______.
(A) 1/2
(B) 1/3
(C) 1/√5
(D) 2/√5

47. cos(A + B + C) = _______.
(A) 1
(B) 0
(C) –1
(D) 1/2

48. If B = cos–1 x, then x = _______.
(A) 1/√5
(B) 3/√10
(C) 1/√10
(D) 2/√5

49. If A = sin–1x; then the value of x is:
(A) 1/√5
(B) 2/√5
(C)1/√10
(D) 3/√10

50. The third angle, ∠C = _______.
(A) π/4
(B) π/3
(C) π/2
(D) 3π/4