Class 12 Mathematics Sample Paper Set B
Please see below Class 12 Mathematics Sample Paper Set B with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.
CBSE Sample Paper for Class 12 Mathematics Set B
PART – A
Section – I
1. Show that the relation R in the set A = {x ∈ Z : 0 ≤ x ≤ 12}, given by R = {(a, b) : a = b} is both symmetric and transitive.
Answer : The set A = {x ∈ Z : 0 ≤ x ≤ 12} = {0, 1, 2, …, 12}
R = {(a, b) : a = b} = {(0, 0), (1, 1), (2, 2),…, (12, 12)}
(i) Let (a, b) ∈ R ⇒ a = b ⇒ b = a
⇒ (b, a) ∈ R.
So, R is symmetric.
(ii) Let (a, b) ∈ R and (b, c) ∈ R ⇒ a = b = c
⇒ a = c ⇒ (a, c) ∈ R.
So, R is transitive.
OR
Give an example of a relation, which is transitive but neither reflexive nor symmetric.
Answer : Let A = {1, 2, 3} and defined a relation R on A as
R = {(1, 2), (2, 2)}.
Then, R is transitive, as (1, 2), (2, 2) ∈ R ⇒ (1, 2) ∈ R
But R is not reflexive, as 1 ∈ A but (1, 1) ∈/ R.
and also R is not symmetric, as (1, 2) ∈ R but (2, 1) ∈/ R.
2. (Image 2)
Answer :

3. Evaluate : (Image 3)
Answer :

OR
Evaluate :
Answer :

4. Find the values of x for which (Image 4)
Answer :
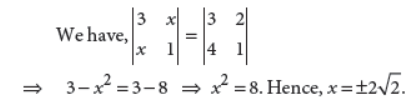
5. Find the equation of a line passing through (1, 2, –3) and parallel to the line x–2/1 = y+1/3 + z–1/4 ,
Answer : Since, the line is parallel to the line x–2/1 = y+1/3 + z–1/4
∴ D.R.’s of the required line are <1, 3, 4>
Hence, equation of the line passing through (1, 2, –3)
with d.r.’s <1, 3, 4> is x–1/1 = y–2/3 + z+3/4
OR
Find the vector equation of the plane passing through a point having position vector 2î + 3ĵ + 4k̂ and perpendicular to the vector 2î + ĵ –k̂.
Answer : Vector equation of plane passing through a point having position vector a̅ and perpendicular to n̅ is given by r̅.n̅ = a.n̅
Here a =2î + 3ĵ + 4k̂ and n̅= 2î + ĵ –k̂
∴ Required equation is r̅.(2î + ĵ –2k̂) = 4+3–8 = –1
6. Prove that the function f : R → R defined by f(x) = 3 – 4x is onto.
Answer : Let y ∈R be any real number, such that f(x) = y.
∴ y = 3 – 4x

7. Find the degree of the differential equation (Image 7)
Answer :

OR
Find the integrating factor of the differential equation (Image 7)
Answer :

8. An urn contains 10 black and 5 white balls. Two balls are drawn from the urn one after the other without replacement, then find the probability that both drawn balls are black.
Answer : Let E and F denote respectively the events that first and second ball drawn are black. We have to find P(E ∩ F).

9. Prove that if E and F are independent events, then the events E′ and F′ are also independent.
Answer : Since, E and F are independent events.
∴ P(E ∩ F) = P(E) P(F) …(i)
Now, P(E′ ∩ F′) = 1 – P(E ∪ F)
[∵ P(E′ ∩ F′) = P((E ∪ F)′)]
= 1 – [P(E) + P(F) – P(E ∩ F)]
= 1 – P(E) – P(F) + P(E) P(F) [Using (i)]
= (1 – P(E)) (1 – P(F)) = P(E′) P(F′)
Hence, E′ and F′ are also independent events.
OR
Given two independent events A and B, such that P(A) = 0.39 and P(B) = 0.6. Find P(A′ ∩ B′).
Answer : Since A and B are independent events, therefore A′ and B′ will also be independent.
So, P(A′ ∩ B′) = P(A′).P(B′) = (1 – P(A)) (1 – P(B))
= (1 – 0.39) (1 – 0.6)
= 0.61 × 0.4
= 0.244
10. The cartesian equation of a line is x+3/2 = y–5/4 = z+6/2 . Find its vector equation.
Answer : The given cartesian equation is x+3/2 = y–5/4 = z+6/2
The line passes through the point (–3, 5, –6) and is parallel to vector 2î + 4ĵ + 2k̂
Hence, the vector equation of the line is r̅ = –3î + 5ĵ –6k̂ + λ(2î + 4ĵ + 2k̂).
11. Let R be a relation on N defined by R = {(1 + x, 1 + x2) : x ≤ 5, x ∈N}. Then, verify the following :
(a) R is reflexive
(b) Domain of R = {2, 3, 4, 5, 6}
Answer : Clearly, R = {(2, 2), (3, 5), (4, 10), (5, 17), (6, 26)}
Domain of R = {x : (x, y) ∈R} = {2, 3, 4, 5, 6}
and R is not reflexive, as 1 ∈ N but (1, 1) ∈/R.
12. Evaluate :
Answer :
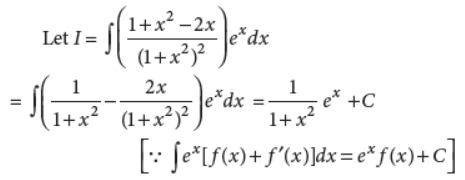
13. If A and B are two events such that P(A) = 0.53, P(B) = 0.24 and P(A ∩ B) = 0.42, then find P(B′ ∩ A).
Answer : P(B′ ∩ A) = P(A – B) = P(A) – P(A ∩ B)
= 0.53 – 0.42 = 0.11
14. If u̅ = î + 2ĵ , v̅ = –2î + 2ĵ and w̅ = 4î + 3ĵ Find scalars x and y respectively such that w̅ = xu̅ + yv̅.
Answer : We have, w̅ = xu̅ + yv̅
⇒ 4î + 3ĵ = x(î + 2ĵ) + y(–2î + ĵ)
⇒ (x −2y − 4)ɵi +(2x + y −3)ɵj = 0
⇒ x – 2y – 4 = 0 and 2x + y – 3 = 0
⇒ x = 2 and y = – 1
15. An urn contains 6 balls of which two are red and four are black. Two balls are drawn at random. Find the probability that they are of the different colours.
Answer : Total number of possible outcomes = 6C2 = 15
Number of favourable outcomes = 2C1 4C1 = 2×4 = 8
∴ Required probability = 8/15
16. Find the additive inverse of A + B, where A and B are given as (Image 16)
Answer :

Section – II
Case study-based questions are compulsory. Attempt any 4 sub parts from each question. Each sub-part carries 1 mark.
17. A cricket match is organised between students of Class XI and Class XII for which a team from each class is chosen. Remaining students of Class XI and XII are respectively sitting on the plane’s represented by the equation r̅.(î + ĵ + 2k̂) = 5 and r̅.(2î – ĵ + k̂) = 8 to cheers the team of their own class.
Based on the above answer the following : (Image )
(i) The cartesian equation of the plane on which student of class XI are seated is
(a) 2x – y + z = 8
(b) 2x + y + z = 8
(c) x + y + 2z = 5
(d) x + y + z = 5
Answer : C
(ii) The magnitude of the normal to the plane on which student of Class XII are seated, is
(a) √5
(b) √6
(c) √3
(d) √2
Answer : B
(iii) The intercept form of the equation of the plane on which student of Class XII are seated, is (Image 17)
Answer : B
(iv) Which of the following is a student of Class XII?
(a) A sitting at (1, 2, 1)
(b) B sitting at (0, 1, 2)
(c) C sitting at (4, 1, 1)
(d) none of these
Answer : C
(v) The distance of the plane, on which student of Class XII are seated, from the origin is
(a) 8 units
(b) 8/√6 units
(c) 5/√6 units
(d) none of these
Answer : B
18. A mobile company in a town has 500 subscribers on its list and collects fix charges of ₹ 300 per year from each subscriber. The company proposes to increase the annual charges and it is believed that for every increase of ₹ 1, one subscriber will discontinue service.
Based on the above information answer the following questions:
(i) If x denote the amount of increase in annual charges of each subscriber,then revenue, R, as a function of x can be represent as
(a) R(x) = 300 × 500 × x
(b) R(x) = (300 – 2x) (500 + 2x)
(c) R(x) = (500 + x) (300 – x)
(d) R(x) = (300 + x) (500 – x)
Answer : D
(ii) If mobile company increases ₹ 50 as annual charges, then R is equal to
(a) ₹ 157500
(b) ₹ 167500
(c) ₹ 17500
(d) ₹ 15000
Answer : A
(iii) If revenue collected by the mobile company is ₹ 156,400, then value of amount increased as annual charges for each subscriber, is
(a) 40
(b) 160
(c) Both (a) and (b)
(d) None of these
Answer : C
(iv) What amount of increase in annual charges will bring maximum revenue?
(a) 100
(b) 200
(c) 300
(d) 400
Answer : A
(v) Maximum revenue is equal to
(a) ₹ 15000
(b) ₹ 160000
(c) ₹ 20500
(d) ₹ 25000
Answer : B
PART – B
Section – III
19. For what value(s) of ‘a’ the matrix (Image 19)
Answer :

⇒ 1(2 – 5) – a (1 –10) + 2(1 – 4) = 0
⇒ –3 + 9a – 6 = 0 ⇒ a = 1
20. Evaluate : (Image 20)
Answer :

OR
Evaluate : (Image 20)
Answer :

21. Find the equation of the tangent to the curve y = x4 – 6x3 + 13x2 – 10x + 5 at the point (1, 3).
Answer : Here, y = x4 – 6x3 + 13x2 – 10x + 5 …(i)
Differentiating (i) w.r.t. x, we get
dy/dx = 4x3–18x2+26x–10
∴ (dy/dx)(1,3) = 4–18+26–10 = 2
Hence the equation of the tangent to (i) at (1, 3) is
y – 3 = 2(x – 1) ⇒ y = 2x + 1
22. Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8.
Answer : Let us draw the graph of given lines, as shown below:


23. Let A and B be two events such that P(A) = 3/8 P(B) = 5/8 and P(A∪B) = 3/4 Find the value of P(A| B)⋅P(A′|B).
Answer :

Also, we know that P(A′ ∩ B) + P(A ∩ B) = P(B)
[As A′ ∩ B and A ∩ B are mutually exclusive events]

OR
Two events E and F are independent. If P(E) = 0.3, P(E ∪ F) = 0.5, then find P(E | F) – P(F | E).
Answer : Since, E and F are independent events.
∴ P(E ∩ F) = P(E) P(F)
⇒ P(E|F) = P(E) and P(F|E) = P(F)
Now, P(E ∪ F) = P(E) + P(F) – P(E ∩ F)
⇒ 0.5 = 0.3 + P(F) – 0.3 P(F)
⇒ P(F)(1 – 0.3) = 0.5 – 0.3 ⇒ P(F) = 0.2/0.7 = 2/7
∴ P(E | F) – P(F | E) = P(E) – P(F)
= 0 3 − 2/7 = 3/10 − 2/7 = 1/70
24. Find the value of sin-1(1/√2) 3sin-1 (√3/2).
Answer :

25. A speaks truth in 60% of the cases and B in 90% of the cases. In what percentage of cases are they likely to contradict each other in stating the same fact?
Answer : Let E = the event of A speaking the truth
and F = the event of B speaking the truth
Then, P(E) = 60/100 = 3/5 and P(F) = 90/100 = 9/10
Required probability = P (A and B contradicting each other)
= P(EF̅ or E̅F) = P(EF̅)+ P(E̅F)
= P(E).P(F̅)+ P(E̅).P(F)
[∵ E and F are independent events]
= P(E) · [1 – P(F)] + [1 – P(E)] · P(F)

26. Find dy/dx for the equation x3 + y3 = sin(x + y).
Answer : We have, x3 + y3 = sin(x + y)
On differentiating both sides w.r.t. x, we get

27. Find the distance between the lines given by r̅ = î + ĵ + λ(î – ĵ + 3k̂) and r̅ = (2î – 3k̂)+μ(î – 2ĵ + 3k̂).
Answer : The given lines are parallel.

28. Solve log (dy/dx) = ax+by.
Answer : We have log (dy/dx) = ax+ay

OR
Solve the differential equation (x+y)2 dy/dx =1.
Answer :


Section – IV
29. Evaluate : (Image 29)
Answer :

30. Consider f : R+ → [4, ∞) given by f(x) = x2 + 4. Show that f is bijective function.
Answer :

31. Find the local maxima or local minima of f(x) = x3 – 6x2 + 9x + 15. Also, find the local maximum or local minimum values as the case may be.
Answer : Given that, f(x) = x3 – 6x2 + 9x + 15
⇒ f ′(x) = 3x2 – 12x + 9.
For local maxima or minima, we must have f ′(x) = 0.
Now, f ′(x) = 0 ⇒ 3(x2 – 4x + 3) = 0
⇒ 3(x – 3)(x – 1) = 0
⇒ x = 3 or x = 1
Case I : When x = 3
In this case, when x is slightly less than 3 then
f ′(x) is negative and when x is slightly more than 3 then f ′(x) is positive.
Thus, f ′(x) changes sign from negative to positive as x increases through 3.
So, x = 3 is a point of local minima.
∴ Local minimum value = f(3) = 15
Case II : When x = 1
In this case, when x is slightly less than 1 then f ′(x) is
positive and when x is slightly more than 1 then f ′(x) is negative.
Thus, f ′(x) changes sign from positive to negative as x increases through 1.
So, x = 1 is a point of local maxima.
∴ Local maximum value = f(1) = 19.
OR
Find the values of x for which the function f(x) = xx, x > 0 is (a) increasing (b) decreasing.
Answer :

32. Find a particular solution of the differential equation cos (dy/dx) = a(aεR); y = 1 when x=0.
Answer :

33. If (Image 33)
Answer : Given, y = Xxx
Taking log on both sides, we get log y = xx log x
Again, taking log on both sides, we get
log (log y) = log(xx log x)
⇒ log (log y) = log xx + log (log x)
⇒ log (log y) = x (log x) + log (log x) …(i)
On differentiating (i) both sides w.r.t. x, we get

34. If a, b are the roots of ax2 + bx + c = 0 and f(x) is continuous at x = a, where f(x) = (Image 34)
Answer : Given, a, b are the roots of ax2 + bx + c = 0,
therefore ax2 + bx + c = a (x – a) (x – b)
Since f (a) is continuous at x = a, therefore

OR
(Image 35) x ≠ 0 then for f to be continuous everywhere, what should be the value of f(0).
Answer :

35. Find the area of the region bounded by the parabola y2 = 4ax, its axis and two ordinates x = a and x = 2a.
Answer : Equation of parabola is y2 = 4ax
Its axis is y = 0 and vertex is (0, 0)

Section – V
36. Solve the following LPP graphically :
Maximize Z = x + y
Subject to the constraints,
2x + 5y ≤ 100
x/25 + y/40 ≤ 1
x ≥ 0, y ≥ 0
Answer : Given problem is
Maximize Z = x + y
Subject to the constraints, x ≥ 0, y ≥ 0, 2x + 5y ≤ 100,
x/25 + y/40 ≤ 1⇒ 8x + 5y ≤ 200
Let us convert the system of the inequations into equations.
l1 : 2x + 5y = 100 and l2 : 8x + 5y = 200
Both the lines intersect at B (50/3 , 40/3)
The solution set of the given system is the shaded region OABC.
The coordinates of corner points O, A, B, C are (0, 0),
(25, 0), (50/3 , 40/3) and (0, 20) respectively.

OR
Find the maximum value of Z = 5x + 2y subject to constraints 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0.
Answer : Let us convert the given inequations into equations and draw the corresponding lines.
We have, 3x + 5y = 15 and 5x + 2y = 10

Thus, Z has maximum value 10 at two points A(2, 0) and B (20/19 , 45/19)
37. Find the equation of the plane passing through the point A(1, 2, 1) and perpendicular to the line joining the points P(1, 4, 2) and Q(2, 3, 5). Also, find the distance of this plane from the line x+3/2 = y–5/–1 = z–7/1.
Answer : The line joining the given points
P(1, 4, 2) and Q(2, 3, 5) has direction ratios
<1 – 2, 4 – 3, 2 – 5> i.e., <– 1, 1, –3>
The plane through (1, 2, 1) and perpendicular to the
line PQ is –1(x – 1) + 1(y – 2) – 3(z – 1) = 0
⇒ x – y + 3z – 2 = 0

OR
Find the coordinates of the points on the line x+2/3 = y+1/2 = z–3/6 , which are at a distance of 2 units from the point (–2, –1, 3).
Answer :

38. If A (Image 38) and f(x) = x2 – 5x – 14, find f(A). Hence obtain A3.
Answer :


OR
Solve the following system of equations by matrix method :
2x + 5y = 1, 3x + 2y = 7
Answer :

