Please see below Class 12 Mathematics Sample Paper Term D Set A with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Term 1 Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.

CBSE Sample Paper for Class 12 Mathematics Term 1 Set D

Section A

In this section, attempt any 16 questions out of Questions 1-20. Each question is of 1 mark weightage.

1. If Δ =

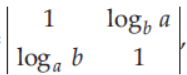
then Δ is equal to
(a) 1
(b) -1
(c) 0
(d) 2

2. If A = [aij ] 2 x 2 , where aij = e2ix sin j x. Then , A is equal to

3. If A and B are square matrices of the same order 3, such that lAl = 3 and AB = 3I, then the value of B is equal to
(a) 2
(b) 3
(c) 9
(d) 1

4. If a function f(x) = sin(8x)/x , x ≠ 0 is continuous at x = 0, then f (0) is equal to
(a) 4
(b) 8
(c) 10
(d) 5

5. The function given by f (x) = 3x³ – 3x² + x – 100 is
(a) increasing on R
(b) decreasing on R
(c) strictly decreasing on R
(d) None of these

6. The point at which the tangent to the curve y = 2×2 – x + 1 is parallel to y = 3x + 9will be
(a) (2, 1)
(b) (1, 2)
(c) (3, 9)
(d) (- 2, 1)

7. If A = [aij] 2 x 2 ,where aij = i2 + 2j2 , then A is equal to

8. Feasible region (shaded) for a LPP is shown in following figure.

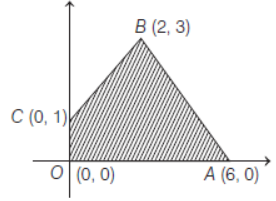
Maximum of Z = 10x – 2y is
(a) 60
(b) 40
(c) 80
(d) 70

9. The function f :N → N, N being the set of natural numbers, defined by f (x) = 2x + 3 is
(a) injective and surjective
(b) injective but not surjective
(c) not injective but surjective
(d) neither injective nor surjective

10. If A is a square matrix satisfying A’ A= I, then the value of lAl² is
(a) – 1
(b) 1
(c) 2
(d) – 2

11. If the domain and range of cosine function are [0, p] and [-1, 1] respectively, then, it is
(a) one-one
(b) onto
(c) both one-one and onto
(d) None of these

12. Find the values of a, b, c and d from the equation

(a) a = 1, b = 3, c = 4 and d = 2
(b) a = 2, b =1, c = 4 and d = 3
(c) a = 1, b = 2, c = 3 and d = 4
(d) a = 1, b = 3 , c = 2 and d = 4

13. Suppose there is a relation R between the positive numbers x and y given by xRy if and only if x ≤ y² . Then, which one of the following is correct?
(a) R is reflexive but not symmetric
(b) R is symmetric but not reflexive
(c) R is neither reflexive nor symmetric
(d) None of the above

14. The value of the constant ‘k’ so that the function f(x) =

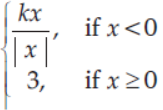
is continuous at x = 0 is
(a) – 3
(b) 0
(c) 3
(d) – 1

15. If the function f(x) =

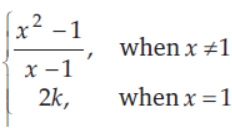
is given to be continuous at x = 1, then the value of k is equal to
(a) 1
(b) 2
(c) 0
(d) – 1

16. If C is a matrix having 2 rows and 3 columns, then number of elements in matrix C is
(a) 6
(b) 3
(c) 2
(d) 5

17. If A =

then|adjA|is equal to
(a) 4³
(b) 4⁶
(c) 4²
(d) 4⁵

18. If matrix A = [a_ij] 3×1 , where a_ij = i³ + j³ , then A is equal to

19. If R and R’ are symmetric relations (not disjoint) on a set A, then the relation RÇ R’ is
(a) not symmetric
(b) symmetric
(c) cannot determine
(d) None of these

20. Let R be a relation on the set N of natural numbers defined by ‘nRmÛnis a factor of m’. Then, which one of the following is correct?
(a) R is reflexive, symmetric but not transitive
(b) R is transitive, symmetric but not reflexive
(c) R is reflexive, transitive but not symmetric
(d) R is an equivalence relation

Section B

In this section, attempt any 16 questions out of Questions 21-40. Each question is of 1 mark weightage.

21. The value of a for which the following is continuous at x = 3:

(a) 9
(b) 12
(c) 3
(d) 15

22. The function f : R → R is defined by f(x) = 3^-x
I. f is one-one function. II. f is onto function.
III. f is a decreasing function.
Which of the above statement(s) is/are correct?
(a) I and II
(b) II and III
(c) I and III
(d) All of these

23. The curve y = xe^x has minimum value equal to
(a) -1/e
(b) 1/e
(c) – e
(d) e

24. The maximum value of Z = 11x + 7y Subject to the constraints 2x + y ≤ 6, x ≤ 2 and x ≥ 0, y ≥ 0 is
(a) 36
(b) 38
(c) 40
(d) 42

25. A trust fund has ₹ 30000 that must be invested in two different types of bonds. The first bond pays 5% interest per year, and the second bond pays 7% interest per year. If the trust must obtain an annual total interest of ₹ 2000, then using matrix multiplication, the amounts invested in two types of bonds are respectively
(a) ₹ 5000 and ₹ 25000
(b) ₹ 25000 and ₹ 5000
(c) ₹ 500 and ₹ 25000
(d) ₹ 5000 and ₹ 2500

26. If Z = 2x + 3y subject to the constraints x + y ≤ 1, x ≥ 0 and y ≥ 0, then maximum of Z is
(a) 1
(b) 2
(c) 3
(d) 4

27. Minimum of Z = 10x – 3y subject to the constraints x + y ≤ 7, 2x – 3y + 6 ≥ 0 and x ≥ 0, y ≥ 0 is
(a) -5
(b) -6
(c) 18
(d) -8

28. Maximum value of Z = 5x + 2y, if the feasible region (shaded) for a LPP is shown in following figure.

(a) 260
(b) 252
(c) 280
(d) 290

29. If A =

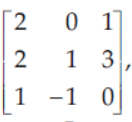
then A² – 5A + 6I is equal to

30. The function f (x) = sin x is
I. strictly increasing in [0,π/2] II. strictly decreasing in [π/2 , π]
III. neither increasing nor decreasing in [0, π ]
(a) I and Il are true
(b) II and III are true
(c) Only II is true
(d) Only III is true

31. The function f (x) = tan-1(sin x + cos x) is an increasing function in
(a) (π/4 , π/2)
(b) (-π/2 , π/4)
(c) (0,π/2)
(d) (-π/2,π/2)

32. The distance between the origin and the normal to the curve y = e²x + x² at x = 0 is
(a) 2 units
(b) √3/2 units
(c) √5/2 units
(d) 2/√5 units

33. If y = log₂ [log₂ (x)], then dy/dx is equal to
(a) log₂e/log_ex
(b) log₂e/x log _x2
(c) log₂x/log_e2
(d) log₂e/x log _ex

34. If

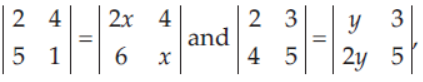
then the value of x + y is
(a) √3 -2
(b) 2 √3
(c) √3 +2
(d) None of these

35. Let f(x) = ex , g(x) = sin^-1 x and h (x) = f [g (x)], then h'(x)/h(x) is equal to
(a) e sin^-1 x
(b) 1√1-x²
(c) sin-1 x
(d) 1/1-x²

36. If f (x) = -3/4 x⁴ – 8x³ – 45/2 x² + 105 , then which of the following holds?
I. f (x) has local maxima at x = 2.
II. f (x) has local maxima at x = 5.
III. f (x) has local minima at x = – 3.
(a) Only I is true
(b) Only III is true
(c) Both I and II are true
(d) All I, II and III are true

37. If y = cos(sin x )² , then at x = √π/2 , dy/dx is equal to
(a) 2
(b) -1
(c) 5
(d) 0

38. If Δ =

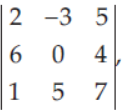
then M₂₁/M₃₂ -1 is equal to
(a) 1
(b) 2
(c) 3
(d) 4

39. If the graphical representation of an LPP is shown below

Then, sum of values of Z = 2x + 3y occurs at all the corner points is
(a) 32
(b) 33
(c) 29
(d) 47

40. If the adjoint of a 3 x 3 non-singular matrix P is

then the possible values of the determinant of P are
(a) ± 2
(b) ± 1
(c) ± 3
(d) ± 4

Section C

In this section, attempt any 8 questions. Each question is of 1 mark weightage. Questions 46-50 are based on Case-Study.

41. If the function f(x) =

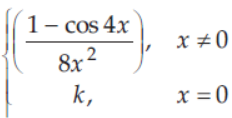
is continuous at x = 0, then the value of k is
(a) 2
(b) -1
(c) 0
(d) 1

42. If y = logsinx(tan x) , then dy/dx at x = π/4 is
(a) 4/log₂
(b) -4/log₂
(c) 1/log₂
(d) None of these

43. If f (x) = logx (loge x ), then f ‘ (x) at x = e is equal to
(a) 1
(b) 2
(c) 0
(d) 1/e

44. Equation of tangent at the curve y be = -x/ a , where it crosses the Y-axis is
(a) x/a + y/b = 1
(b) x/a – y/b = 1
(c) x²/a² + y²/b² = 1
(d) x²/a² – y²/b² = 1

45. The points at which the tangent passes through the origin for the curve y = 4x³ – 2x⁵ are
(a) (0, 0), (2, 1) and (-1, -2)
(b) (0, 0), (2, 1) and (- 2, – 1)
(c) (2, 0), (2,1) and (- 3 , 1)
(d) (0, 0), (1,2) and (- 1, -2)

CASE STUDY

For awareness on Covid-19 protocol, Indian Government planned to fix a hoarding board at the face of a building on the road of a busy market. Sagar, Roy and Asif are the three engineers who are working on the project, P and P’ are considered to be two person viewing the hoarding board 40 m and 50 m respectively, away from the building. All three engineers suggested to the firm to place the hoarding board at three different locations namely R, S and T. R is at the height of 20 m from the ground level. For the viewer P, the angle of elevation of S is double the angle of elevation of R. The angle of elevation of T is triple the angle of elevation of R for the same viewer.
Look at the given figure.

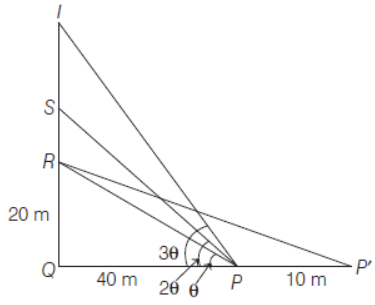
Based on the above information, answer the following questions.

46. Measure of ∠RPQ is equal to
(a) tan-1(3)
(b) tan-1(1)
(c) tan-1(1/2)
(d) tan-1(2)

47. Measure of ∠SPQ is equal to
(a) tan-1(4)
(b) tan-1(4/3)
(c) tan-1(3)
(d) tan-1(3/4)

48. Measure of ∠TPQ is equal to
(a) tan^-1(11/2)
(b) tan^-1(2/11)
(c) tan^-1(3)
(d) tan^-1(11)

49. Measure of ∠RP’Q is equal to
(a) tan-1(1/5)
(b) tan-1(2/3)
(c) tan-1(3/2)
(d) tan-1(2/5)

50. Domain and Range of tan-1 is equal to
(a) R,(0 , π/2)
(b) R,(-π/2 , π/2)
(c) R^– ,(-π/2 , π/2)
(d) R⁺ ,(-π/2 , π/2)