Class 12 Mathematics Sample Paper Set H
Please see below Class 12 Mathematics Sample Paper Set H with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.
CBSE Sample Paper for Class 12 Mathematics Set H
SECTION – A
1. Form the differential equation representing the family of curves y=A/x+5, by eliminating the arbitrary constant A.
Sol. y=A/x+5
⇒ (y − 5)x = A
⇒ (y − 5) × 1 + x × dy/dx = 0
∴ dy/dx = 5−y/x .
2. If A is a square matrix of order 3, with A = 9 , then write the value of |2adj.A| .
Sol. |2adj.A| = 23 |adj.A| = 8 |A|3−1 = 8 × 92 = 648.
3. Find the acute angle between the planes r̅.(î − 2ĵ− 2k̂) =1 and r̅.(3î − 6ĵ+ 2k̂ ) = 0 .
Sol. The angle between the two planes is same as the angle between their normal vectors.
The normals of the given planes are î − 2ĵ− 2k̂ and 3î − 6ĵ+ 2k̂ .

OR
Find the length of the intercept, cut off by the plane 2x + y − z = 5 on the x-axis.
Sol. For x-intercept, put y = 0, z = 0 in 2x + y − z = 5
∴ x = 5/2 = x-intercept
4. If y log(cos ex ), then find dy/dx.
Sol. y = log(cos ex )
∴ dy/dx = 1/cos ex × (−sinex) × ex = −ex tan ex.
SECTION – B
5. Find :
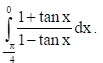
Sol.

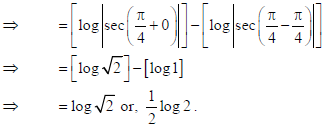
6. Let * be an operation defined as *:R×R→R such that a *b = 2a + b, a, b ∈ R. Check if * is a binary operation. If yes, find if it is associative too.
Sol. As a, b ∈ R ∴ 2a + b ∈ R . That is, a *b ∈ R .
Hence, * is a binary operation.
Now (a *b)*c = (2a + b)*c, a,b,c ∈ R
⇒ (a *b)*c = 4a + 2b + c
Also, a *(b*c) = a *(2b + c) = 2a + 2b + c ≠ (a *b)*c .
Hence, * isn’t associative.
7. X and Y are two points with position vectors 3a̅ + b̅ and a̅ −3b̅ respectively. Write the position vector of a point Z which divides the line segment XY in the ratio 2 : 1 externally.
Sol.
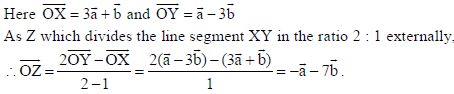
OR
Let a̅ = î + 2ĵ− 3k̂ and b̅ = 3î − ĵ+ 2k̂ be two vectors. Show that the vectors a̅ + b̅ and a̅ − b̅ are perpendicular to each other.
Sol. If a̅ + b̅ and a̅ − b̅ are perpendicular to each other then, (a̅ + b̅).(a̅ − b̅) = 0
Now (a̅ + b̅).(a̅ − b̅) = a̅.a̅ − a̅.b̅ + b̅.a̅ − b̅.b̅ = |a̅|2 − |b̅|2 = |î + 2ĵ−3k̂|2 − |3î − ĵ+ 2k̂|2
⇒ = (1+ 4 + 9) − (9 +1+ 4) = 0.
Hence, a̅ + b̅ and a̅ − b̅ are perpendicular to each other.
8. If A and B are symmetric matrices, such that AB and BA are both defined, then prove that AB− BA is a skew symmetric matrix.
Sol. We have (AB− BA)T = (AB)T − (BA)T = BTAT −ATBT = BA−AB = −(AB− BA)
[As A and B are symmetric matrices so, AT = A, BT = B.
Hence, AB− BA is a skew symmetric matrix.
9. 12 cards numbered 1 to 12 (one number on one card), are placed in a box and mixed up thoroughly. Then a card is drawn at random from the box. If it is known that the number on the drawn card is greater than 5, find the probability that the card bears an odd number.
Sol. Let A : the card bears odd number and B : number on the card is greater than 5.
Clearly A ={1,3,5,7,9,11}, B ={6,7,8,9,10,11,12} and A∩B ={7,9,11}

10. Out of 8 outstanding students of a school, in which there are 3 boys and 5 girls, a team of 4 students is to be selected for a quiz competition. Find the probability that 2 boys and 2 girls are selected.
Sol.

OR
In a multiple choice examination with three possible answers for each of the five
questions, what is the probability that a candidate would get four or more correct answers just by guessing?
Sol. Here n = 5,
p = probability of getting correct answer by guessing, from 3 possible answers = 1/3

11. Solve the following differential equation :
dy/dx + y = cos x − sin x
Sol. The D.E. is of the form dy/dx + P(x)y = Q(x), where P(x) = 1, Q(x) cos x − sin x
∴ I.F. = e∫1dx = ex
The solution is given by ex × y = ∫ex ×(cos x − sin x)dx +C
∴ ex × y = ex ×(cos x) + C or, y = cos x + Ce−x [∵ ∫ex{f (x) + f ‘(x)}dx = exf (x) + C
12. Find : ∫x tan−1 x dx .
Sol.

OR
Find :
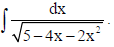
Sol.

SECTION – C
13. Using properties of determinants, find the value of x, for which

Sol.

On expanding along C1 , we get
0 − 0 + (12 + x)(4x2 − 0) = 0
Either (12 + x) = 0 or, 4x2 = 0
∴x = 0 or,−12 .
14. Solve the differential equation dy/dx = 1 + x2 + y2 + x2y2 , given that y =1 when x = 0.
Sol.

OR
Find the particular solution of the differential equation dy/dx = xy / x2 + y2 given that y =1
when x = 0 .
Sol.


15. Let A = R −{2} and B = R −{1}. If f :A→B is a function defined by f (x) = x −1/x−2, show that f is one-one and onto. Hence, find f −1 .
Sol.

OR
Show that the relation S in the set A ={x ∈ Z: 0 ≤ x ≤12} given by
S ={(a,b) : a,b ∈ A, |a − b| is divisible by 3} is an equivalence relation.
Sol. S ={(a,b) : a,b ∈ A, |a − b| is divisible by 3} is defined on the set A ={x ∈ Z: 0 ≤ x ≤12}.
Clearly, S is reflexive, as 3 divides |a − a| = 0 , for all a ∈ A.
Further if (a, b) ∈ S, then 3 divides |a − b| . Therefore, 3 divides −(b − a) = b − a as well.
Hence, (b, a) ∈ S, which follows that S is symmetric.
Similarly, if (a, b) ∈ S and (b, c) ∈ S, then |a − b| and |b − c| are both divisible by 3.
That is, |a − b| = 3m i.e., a − b = ±3m and |b − c| = 3n i.e., b − c = ± 3n
So, (a − b) + (b − c) = a − c = ±3(m+ n) ⇒ |a − c| = 3(m+ n)
Therefore, |a − c| is divisible by 3.
This shows that S is transitive as (a, c) ∈ S.
Thus, S is an equivalence relation in the set A.
16.

Sol.

17. If x = sin t, y = sin pt , prove that

Sol. We have x = sin t, y = sin pt
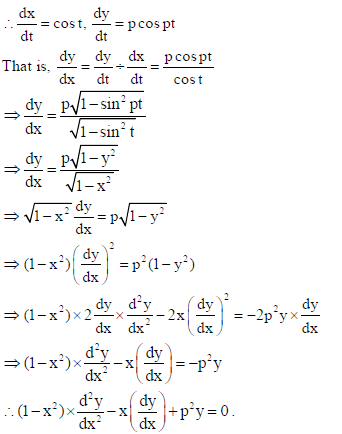
OR
Sol.

18. Prove that :
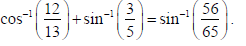
Sol.
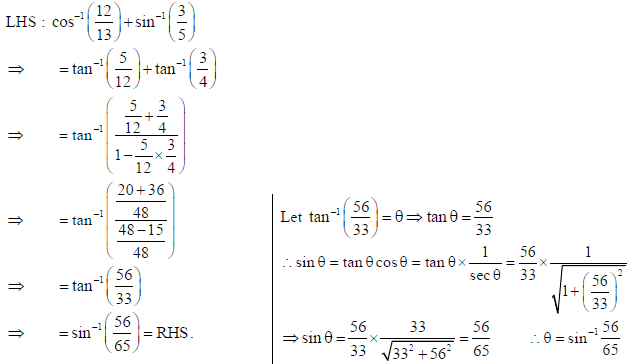
19. If y = (x)cosx + (cos x)sin x , find dy/dx.
Sol.

20. Prove that

Sol.


21. Find the value of x, for which the four points A(x, –1, –1), B(4, 5, 1), C(3, 9, 4) and D(–4, 4, 4) are coplanar.
Sol.
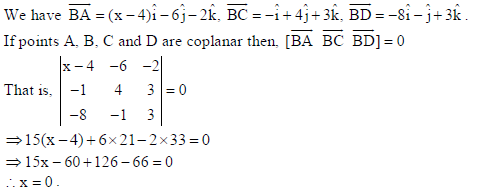
22. A ladder 13 m long is leaning against a vertical wall. The bottom of the ladder is dragged away from the wall along the ground at the rate of 2 cm/sec. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall?
Sol. Consider the ladder of 13 m length be AB.
Also let at any time t, the lower end of the ladder be at a distance of x m from the wall BC and at
that moment, its height on the wall be y m
Consider the figure shown.
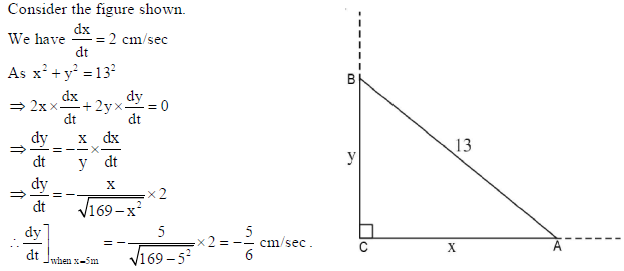
Hence the height on the wall is decreasing at the rate of 5/6 cm/sec.
23. Find the vector equation of the plane determined by the points A(3, –1, 2), B(5, 2, 4) and C(–1, –1, 6). Hence find the distance of the plane, thus obtained, from origin.
Sol. Equation of plane determined by A(3, –1, 2), B(5, 2, 4) and C(–1, –1, 6) is
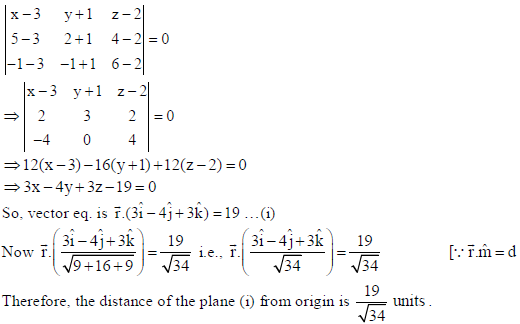
SECTION – D
24. Using integration, find the area of the greatest rectangle that can be inscribed in an ellipse


25. An insurance company insured 3000 cyclists, 6000 scooter drivers and 9000 car drivers. The probability of an accident involving a cyclist, a scooter driver and a car driver are 0.3, 0.05 and 0.02 respectively. One of the insured persons meets with an accident. What is the probability that he is a cyclist?
Sol. Let the events are defined as E1 : Person chosen is a cyclist,
E2 : Person chosen is a scoter-driver,
E3 : Person chosen is a car driver and,
A : Person meets with an Accident.

26. Using elementary row transformations, find the inverse of the matrix
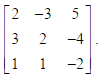
Sol.
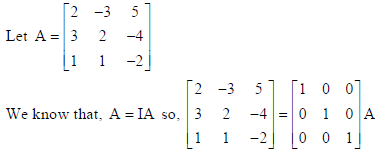

OR
Using matrices, solve the following system of linear equations :
x + 2y − 3z = −4,
2x + 3y + 2z = 2,
3x −3y − 4z = 11.
Sol.
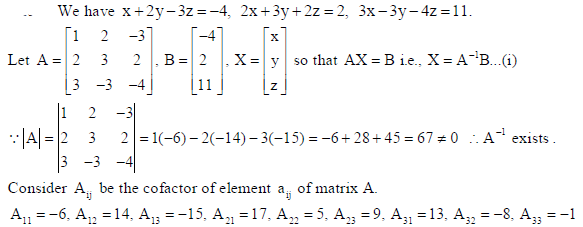
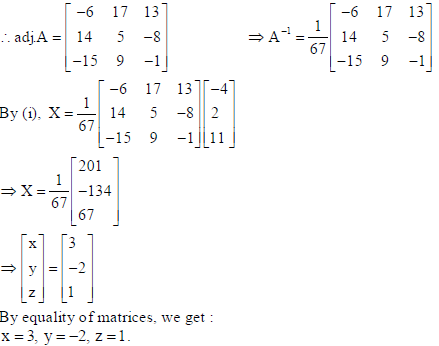
27. Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9 .
Sol.

OR
Using the method of integration, find the area of the region bounded by the lines
3x − 2y +1= 0, 2x + 3y − 21= 0 and x − 5y + 9 = 0 .
Sol.

28. A dietician wishes to mix two types of food in such a way that the vitamin contents of the mixture contains at least 8 units of vitamin A and 10 units of vitamin C. Food I contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C. It costs `50 per kg to produce food I. Food II contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C and it costs `70 per kg to produce food II. Formulate this problem as a LPP to minimize the cost of a mixture that will produce the required diet. Also find the minimum cost.
Sol. Let the dietician mix x kg of food I and y kg of food II.
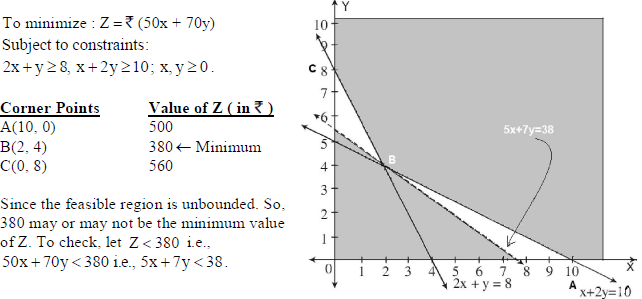
Note that the feasible region and 5x + 7y < 38 do not have any common point.
∴ Minimum value of Z is `380 when x = amount of food I = 2 kg and, y = amount of food II = 4 kg .
29. Find the vector equation of a line passing through the point (2, 3, 2) and parallel to the line r̅ = (−2î + 3ĵ) + λ(2î −3ĵ+ 6k̂ ) . Also, find the distance between these lines.
Sol. As the d.r.’s of parallel lines are proportional so, the equation of line passing through (2, 3, 2)
and parallel to r̅ = (−2î + 3ĵ) + λ(2î −3ĵ+ 6k̂ ) is : r̅ = (2î + 3ĵ+ 2k̂ ) + λ(2î − 3ĵ+ 6k̂) .
Now a̅1 = −2î + 3ĵ, a̅2 = 2î + 3ĵ+ 2k̂, b̅ = 2î −3ĵ+ 6k̂
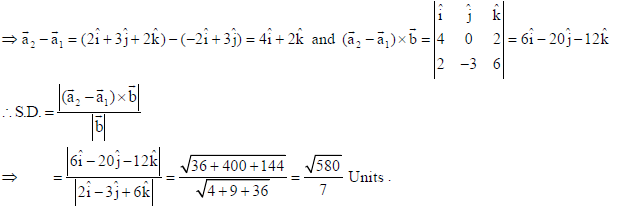
OR
Find the coordinates of the foot of the perpendicular Q drawn from P(3, 2, 1) to the plane 2x − y + z +1= 0 . Also, find the distance PQ and the image of the point P treating this plane as a mirror.
Sol.

