Three Dimensional Geometry MCQ Questions Class 12 Mathematics
Please refer to MCQ Questions for Class 12 Mathematics Chapter 11 Three Dimensional Geometry with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 12 Mathematics. Students should refer to MCQ Questions for Class 12 Mathematics with Answers to score more marks in Grade 12 Mathematics exams. Students should read the chapter Three Dimensional Geometry and then attempt the following objective questions.
Please refer to MCQ Questions for Class 12 Mathematics Chapter 11 Three Dimensional Geometry with answers below.
MCQ Questions for Class 12 Mathematics Chapter 11 Three Dimensional Geometry with answers
MCQ Questions for Class 12 Mathematics Chapter 11 provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. The distance of the plane 2x y z − + + = 3 6 14 0 from the origin is
(a) 14
(b) 2
(c) –2
(d) 11
Answer
B
Question. The equation of plane which passes through the points (2, 3, –4) and (1, –1, 3) and parallel to x-axis, is
(a) 7y -4z – 50 =0
(b) 4y- 7z- 5 =0
(c) 4y+ 7z +5=0
(d) 7y+ 4z- 5 =0
Answer
D
Question. The equation of the plane through the points (–1, 1, 1), (1, –1, 1) and perpendicular to the plane x+2y +2z = 5, is
(a) 2x -2y-3z +3=0
(b) 2x -2y+3z -3=0
(c) x +y-3z +3=0
(d) 2x +2y-3z +3=0
Answer
D
Question. From the point P( a, b, c ) the normals drawn to planes YZ ZX and are PA PB and respectively, then the equation of plane OAB is
(a) bcx +acy+ abz = 0
(b) bcx- acy + abz = 0
(c) bcx+acy +abz = 0
(d) − bcx +acy+ abz = 0
Answer
B
Question.

Answer
C
Question. The equation of the plane passing through the points (3, 2, –1), (3, 4, 2) and (7, 0, 6) is 5x+3y-2z= λ , where λ is equal to
(a) 23
(b) 25
(c) 20
(d) –27
Answer
A
Question. If the DC’s of a line are (1/c,/c, 1/c), then
(a) c < 0
(b) c = ± √3
(c) 0 <c<1.5
(d) c > 2
Answer
B
Question. The cartesian equation of the plane
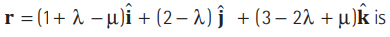
(a) 2x+ y=5
(b) 2x-y=5
(c) 2x+z=5
(d) 2x-z=5
Answer
C
Question. The equation of the plane passing through the point (–1, 3, 2) and perpendicular to planes x+ 2y+ 3z = 5 and 3x +3y+z=9, is
(a) 7X- 8Y- 3Z+ 25 =0
(b) 7X- 8Y + 3Z+ 25 =0
(c) 7X-8Y + 3Z +25 = 0
(d) 7X+8Y +3Z – 25 = 0
Answer
B
Question. Ratio in which the xy-plane divides the join of (1, 2, 3) and (4, 2, 1) is
(a) 3 : 1internally
(b) 3 : 1 externally
(c) 1 : 2 internally
(d) 2 : 1 internally
Question. The shortest distance between lines x-3/3= y-8/-1=y-8/-1=z-3/-3= and x+3,-3 = y+7/2= z-6/4 is
(a) 3√30
(b) √30
(c) 2√30
(d) 4√30
Answer
A
Question. The equation of the line passing through the point (1, 2, 3) and perpendicular to x+ 2y -5z + 9= 0 is
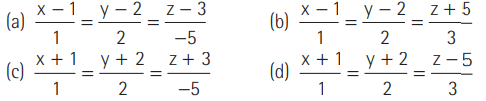
Answer
A
Question. The point of intersection of the line x/1= y-1/2= z+2/3 and plane 2x+3y+z=0 is
(a) (0, 1, –2)
(b) (1, 2, 3)
(c) (–1, 9, –25)
(d) (-1/11, 9/11,- 25/11)
Answer
D
Question. The length of perpendicular from (2,1,5) to the line x-11/10= y+2/-4= z+8/-11 and the coordinates of the foot are
(a) √14, (1, 2, -3)
(b) √14, (1, 2, 3)
(c) √14, (1, 2, 3)
(d) None of these
Answer
C
Question. The equation of perpendicular from (3, –1, 11) to the line
(a) x-3/1= y+1/-6= z-11/4
(b) x-3/1= y+1/6 = z-11/4
(c) x+3/-1 = y+1/-6 = z-11/4
(d) x+3/-1= y+1/-6= z-11/4
Answer
A
Question. If a, b andc are three unit vectors equally inclined to each other at angle θ. Then, angle between a and the plane of b and c is
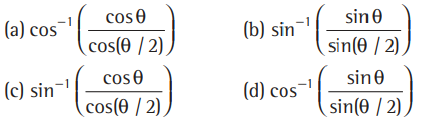
Answer
A
Question. The plane x -y- z = 4 is rotated through an angle 90° about its line of intersection with the plane x+ y+ 2z = 4. Then, the equation of the plane in its new position is
(a) x+y + 4z =20
(b) x+ 5y+ 4z =20
(c) x+ y- 4z =20
(d) 5x+ y+ 4z=20
Answer
D
Question.

(a) 1/4
(b) −1/4
(c) 1/8
(d) −1/8
Answer
A
Question. Let the vectors, a, b, c and d be such that (a xb) x(c x d) = 0. Let P1 and P2 be planes determined by the pairs of vectors a, b and c, d respectively. Then, the angle between p1 and p2
(a) 0
(b) π/4
(c) π/3
(d) π/2
Answer
A
Question. Two systems of rectangular axes have the same origin. If plane cut the intercepts a’, b’, c′ on coordinates axes for Ist system and intercepts a’,b’,c′ on 2nd system, then pick the correct alternatives

Answer
A
Question. A variable plane at a distance of the one unit from the origin cuts the coordinates axes at A B, and C. If the centroid D (x, y,) z of ∆ ABC satisfies the relation 1/x2 + 1/y2+1/z;=k, , then the value of k is
(a) 3
(b) 1
(c) 1/3
(d) 9
Answer
D
Question. The line x+2y – z-3=0, x+3y -z -4 =0 is parallel to
(a) xy-plane
(b) yz-plane
(c) zx-plane
(d) z-axis
Answer
C
Question. Under what condition does a straight line//50 is parallel to the xy-plane ?
(a) l = 0
(b) m = 0
(c) n = 0
(d) l = 0, m = 0
Answer
C
Question. There is a point P(a ,a ,a ) on the line passing through the origin and equally inclined with axes. The equation of plane perpendicular to OP and passing through P cuts the intercepts on axes. The sum of whose reciprocals is
(a) a
(b) 3/2 a
(c) 3a/a
(d) 1/a
Answer
D
Question. The equation of the plane through the points (1, 2, 3),(– 1, 4, 2) and (3, 1,1) is
(a) 5x+y+ 12z -23=0
(b) 5x+ 6y + 2z -23 =0
(c) x+ 6y +2z-13=0
(d) x+ y+ z −13 = 0
Answer
B
Question. If a plane meets the coordinate axes at A , B and C such that the centroid of the triangle is (1, 2, 4), then the equation of the plane is
(a) x+ 2y +4z=12
(b) 4x+2y+z=12
(c) x+2y +4z =3
(d) 4x+2y+z = 3
Answer
B
Question. If for a plane, the intercepts on the coordinate axes are 8, 4, and 4, then the length of the perpendicular from the origin to the plane is
(a) 8 /3
(b) 3/ 8
(c) 3
(d) 4 /3
Answer
A
Question. If the distance of the point (1, 1, 1) from the origin is half its distance from the plane x+ y+ z+ k = 0, then k is equal to
(a) ± 3
(b) ± 6
(c) 3, -9
(d) 3, -9
Answer
D
Question. The equation of the plane through the intersection of the planes x+ y +z = 1 and 2x+ 3y-z+4=0 parallel to x-axis is
(a) y- 3z+ 6 =0
(b) 3y- z+ 6 =0
(c) y+ 3z + 6 =0
(d) 3y-2z + 6=0
Answer
A
Question. A plane makes intercepts 3 and 4 respectively on z-axis and x-axis. If plane is parallel to y-axis, then its equation is
(a) 3x+ 4z =12
(b) 3z+4x=12
(c) 3y+4z =12
(d) 3z+4y=12
Answer
A
Question. The equation of the plane which bisects the line joining (2, 3, 4) and (6, 7, 8), is
(a) x – y – z – 15 = 0
(b) x- y+ z − 15 = 0
(c) x+ y + z – 15 = 0
(d) x + y+ z + 15 = 0
Answer
C
Question. The points A( -1,3,0), B(2,2,1) and C(1,1,3) determine a plane. The distance from the plane to the point D( 5,7,8) is
(a) √66
(b) √71
(c) √73
(d) √76
Answer
A
Question. Equation of the plane which passes through the line of intersection of the planes P = ax+ by+ c z+ d =0, P’ =a’ x +b’ y+ c’ z +d ′ = 0 and parallel to x-axis, is
(a) Pa -P’ a’ = 0
(b) P/a =’p’/a’= 0
(c) Pa + P’ a’ = 0
(d) p/a = p’/a’
Answer
D
Question. If M denotes the mid-point of the line joining

Answer
A
Question. If the foot of the perpendicular from the origin to a plane is ( a,b,c), then equation of the plane is
(a) x/a +y/b + z/c=1
(b) ax +by+ c z =1
(c) ax +by +c z=a2+b2+c2
(d) ax by +c z = 0
Answer
C
Question.

(a) acute angles
(b) obtuse angles
(c) right angles
(d) None of these
Answer
A
Question. The shortest distance between the lines

(a) √29 units
(b) 29 units
(c) √29/2/units
(d) 2 √29 units
Answer
D
Question. Distance of the point (α, β, γ) from y-axis is
(A) b
(B) |b|
(C) |b|+ |g|

Answer
D
Question. If the direction cosines of a line are k, k, k, then

Answer
D
Question. The distance of the plane
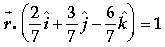
from the origin is
(A) 1
(B) 7
(C) 1/7
(D) None of these
Answer
A
Question. The reflection of the point (α, β, γ) in the xy-plane is
(A) (α, β, 0)
(B) (0, 0, γ)
(C) (–α, –β, γ)
(D) (α, β, –γ)
Answer
D
Question. The area of the quadrilateral ABCD, where A(0, 4, 1), B(2, 3, –1), C(4, 5, 0) and D(2, 6, 2), is equal to
(A) 9 sq. units
(B) 18 sq. units
(C) 27 sq. units
(D) 81 sq. units
Answer
A
Read the following text and answer the following questions on the basis of the same:
The Indian coast guard, while patrolling, saw a suspicious boat with people. They were nowhere looking like fishermen. The coast guard were closely observing the movement of the boat for an opportunity to seize the boat. They observed that the boat is moving along a planar surface. At an instant of time, the coordinates of the position of the coast guard helicopter and the boat is (1, 3, 5) and (2, 5, 3) respectively

We hope you liked the above MCQ Questions for Class 12 Mathematics Chapter 11 Three Dimensional Geometry. In case you have any questions please put them in the comments box below and our teache
Question. If the line joining the positions of the helicopter and the boat is perpendicular to the plane in which the boat moves, then the equation of the plane is
(A) –x + 2y – 2z = 6
(B) x + 2y + 2z = 6
(C) x + 2y – 2z = 6
(D) x – 2y – 2z = 6
Answer
C
Question. If the coast guard decide to shoot the boat at that given instant of time, then what is the distance (in meters) that the bullet has to travel?
(A) 5 m
(B) 3 m
(C) 6 m
(D) 4 m
Answer
B
Question. If the coast guard decides to shoot the boat at that given instant of time, when the speed of bullet is 36 m/sec, then what is the time taken for the bullet to travel and hit the boat?
(A) 1/8 seconds
(B) 1/14 seconds
(C) 1/10 seconds
(D) 1/12 seconds
Answer
D
Question. At that given instant of time, the equation of line passing through the positions of the helicopter and boat is

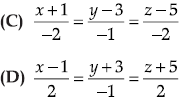
Answer
A
Question. At a different instant of time , the boat moves to a different position along the planar surface . What should be the coordinates of the location of the boat if the coast guard shoots the bullet along the line whose equation is
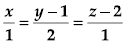
for the bullet to hit the boat

Answer
D
Read the following text and answer the following questions on the basis of the same :
Suppose the floor of a hotel is made up of mirror polished Salvatore stone . There is a large crystal chandelier attached to the ceiling of the hotel room . Consider the floor of the hotel room as a plane having the equation x – y + z = 4 and the crystal chandelier is suspended at the point ( 1 , 0 , 1 ) .

Question. Find the direction ratios of the perpendicular from the point (1, 0, 1) to the plane x – y + z = 4.
(A) (–1, –1, 1)
(B) (1, –1, –1)
(C) (–1, –1, –1)
(D) (1, –1, 1)
Ans. Option (D) is correct.
Question. Find the length of the perpendicular from the point (1, 0, 1) to the plane x – y + z = 4.
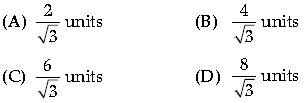
Ans. Option (A) is correct.
Question. The equation of the perpendicular from the point (1, 0, 1) to the plane x – y + z = 4 is

Ans. Option (C) is correct
Question. The equation of the plane parallel to the plane x – y + z = 4, which is at a unit distance from the point (1, 0, 1) is
(A) x – y + z + (2 – 3)
(B) x – y + z – (2 + 3)
(C) x – y + z + (2 + 3)
(D) Both (A) and (C)
Answer
D
Question. The direction cosine of the normal to the plane x – y + z = 4 is

Answer
B
Read the following text and answer the following questions on the basis of the same:
A mobile tower stands at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1) on it. The mobile tower is tied with 3 cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at the point (2, 3, 1) as shown in the figure.

Question. The equation of the plane passing through the points A, B and C is
(A) 3x – 2y + 4z = –11
(B) 3x + 2y + 4z = 11
(C) 3x – 2y – 4z = 11
(D) –3x + 2y + 4z = –11
Ans. Option (B) is correct.
Answer
B
Question. The height of the tower from the ground is

Answer
A
Question. The equation of the perpendicular line drawn from the top of the tower to the ground is

Answer
C
Question. The co-ordinates of the foot of the perpendicular drawn from the top of the tower to the ground are

Answer
D
Question. The area of ΔABC is

Answer
B
Read the following text and answer the following questions on the basis of the same:
P1 : x + 3y – z = 0 and P2 : y + 2z = 0 are two intersecting planes. P3 is a plane passing through the point (2, 1, –1) and through the line of intersection of P1 and P2.

Question. Find the direction cosines of the plane P3.

Answer
B
Question. Equation of P3 is _______.
(A) 4x + y – 2z = 10
(B) x + y – 2z = 3
(C) x + 9y + 11z = 0
(D) 4x – y + z = 0
Answer
C
Question. Equation of plane parallel to P3 and passing through (1, 2, 3) is _______.
(A) x + 9y + 11z – 52 = 0
(B) x + 9y + 11z – 20 = 0
(C) 4x + y – 2z + 10 = 0
(D) 4x + y – 2z + 1 = 0
Answer
A
Question. ______ is a point on P3.
(A) (1, 2, 3)
(B) (–1, 4, 3)
(C) (–6, –3, 3)
(D) (6, 3, –3)
Answer
C
Question. Distance of P3 from origin is _______ units.
(A) 0
(B) 1
(C) 1/√5
(D) 11/10
Answer
A
Read the following text and answer the following questions on the basis of the same:
Consider the plane p1: 2x – 3y + 4z + 9 = 0 and the point P(1, –2, 3). p1 is a plane parallel to p2 and containing the point P.

Question. Equation of is
(A) 2x – 3y + 4z +9 = 0
(B) 2x – 3y + 4z + 20 = 0
(C) 2x – 3y + 4z – 20 = 0
(D) 2x – 3y + 4z – 9 = 0
Answer
C
Question. Distance between π₁ and π₂ is
(A) 5
(B) √29
(C) √13
(D) 2√3 units .
Answer
B
Question. A is the foot of perpendicular from P to π₁ . Equation of PA is
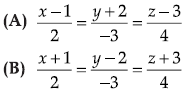
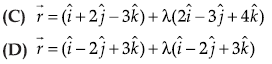
Answer
A
Question. The co – ordinates of A are
( A ) ( 0 , 0 , 0 )
( B ) ( -1,2,3 )
( C ) ( -1 , 1 , -1 )
( D ) ( 1, 4 , -2 )
Answer
C
Question. The image of P on π1 is
(A) ( -1 , 1 , -1 )
(B) ( -1,2 , -3 )
(C) ( -3,4 , -5 )
(D) ( 0 , 0 , 0 )
Answer
C
