Class 12 Mathematics Sample Paper Set K
Please see below Class 12 Mathematics Sample Paper Set K with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.
CBSE Sample Paper for Class 12 Mathematics Set K
1.
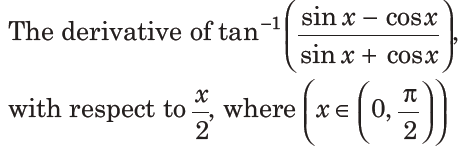
(a) 1
(b)2/3
(c)1/2
(d) 2
Answer
D
2. For an initial screening of an admission test, a candidate is given fifty problems to solve. If the probability that the candidate can solve any problem is 4/5 , then the probability that he is unable to solve less than two problem is
(a) 201/5(1/5)49
(b)316/25(4/5)48
(c)54/5(4/5)49
(d) 164/25(1/5)48
Answer
C
3. A value of a such that
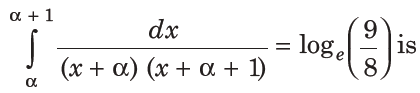
(a) – 2
(b)1/2
(c) – 1/2
(d) 2
Answer
A
4. Let α ∈(0, π / 2) be fixed. If the integral
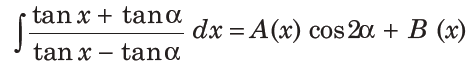
sin 2α + C, where C is a constant of integration, then the functions A(x) and B(x) are respectively
(a) x + α and loge |sin(x+α)
(b) x – α and loge |sin(x-α)|
(c) x – α and loge |cos(x-α)|
(d) x + α and loge |sin(x-α)|
Answer
B
5. The angle of elevation of the top of a vertical tower standing on a horizontal plane is observed to be 45° from a point A on the plane. Let B be the point 30 m vertically above the point A.
If the angle of elevation of the top of the tower from B be 30°, then the distance (in m) of the foot of the tower from the point A is
(a) 15 (3 + √3)
(b) 15(5 – √3)
(c) 15(3 – √3)
(d) 15 (1 + √3)
Answer
A
6. Let S be the set of all a ∈R such that the equation, cos2x + α sin x = 2α – 7 has a solution. Then, S is equal to
(a) R
(b) [1, 4]
(c) [3, 7]
(d) [2, 6]
Answer
D
7. A plane which bisects the angle between the two given planes 2x – y + 2z – 4 = 0 and x + 2y + 2z – 2 = 0, passes through the point
(a) (1, – 4, 1)
(b) (1, 4, – 1)
(c) (2, 4, 1)
(d) (2, – 4, 1)
Answer
D
8.
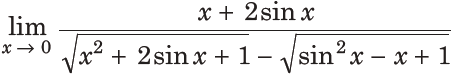
(a) 6
(b) 2
(c) 3
(d) 1
Answer
B
9. A group of students comprises of 5 boys and n girls. If the number of ways, in which a team of 3 students can randomly be selected from this group such that there is at least one boy and at least one girl in each team,is 1750, then n is equal to
(a) 28
(b) 27
(c) 25
(d) 24
Answer
C
10. An ellipse, with foci at (0, 2) and (0, – 2) and minor axis of length 4,passes through which of the following points?
(a) ( √2, 2)
(b) (2, √2)
(c) (2,2 √2)
(d) (1, 2 √2)
Answer
A
11. The boolean expression ~ (p ⇒ (~q)) is equivalent to
(a) p ∧ q
(b) q ⇒~ p
(c) p v q
(d) (~ p) ⇒ q
Answer
A
12. A circle touching the X-axis at (3, 0) and making a intercept of length 8 on theY-axis passes through the point
(a) (3, 10)
(b) (3, 5)
(c) (2, 3)
(d) (1, 5)
Answer
A
13.
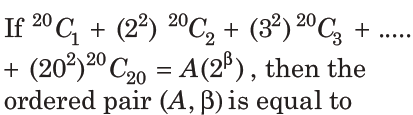
(a) (420, 19)
(b) (420, 18)
(c) (380, 18)
(d) (380, 19)
Answer
B
14. A value of q ∈(0, π / 3), for which
(a)π/9
(b)π/18
(c)7π/24
(d)7π/36
Answer
A
15. The equation of a common tangent to the curves, y2 = 16 and xy = – 4, is
(a) x – y + 4 = 0
(b) x + y + 4 = 0
(c) x – 2y + 16 = 0
(d) 2x – y + 2 = 0
Answer
A
16. Let z ∈ C with I m (z) = 10 and it satisfies
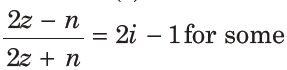
natural number n, then
(a) n = 20 and Re(z) = – 10
(b) n = 40 and Re(z) = 10
(c) n = 40 and Re(z) = – 10
(d) n = 20 and Re(z) = 10
Answer
C
17. A triangle has a vertex at (1, 2) and the mid-points of the two sides through it are (-1, 1) and (2, 3). Then, the centroid of this triangle is
Answer
B
18. If a1, a2, a3,… are in AP such that a1+a7+a16=40, then the sum of the first 15 terms of this AP is
(a) 200
(b) 280
(c) 120
(d) 150
Answer
A
19. If [x]denotes the greatest integer ≤ x ,then the system of liner equations [sin θ]x + [- cosθ]y = 0, [cot θ]x + y = 0
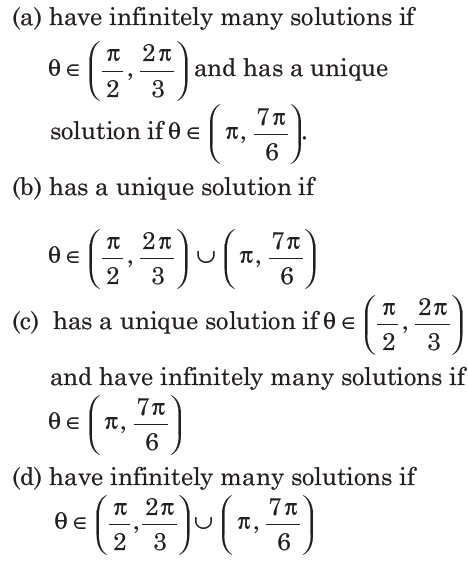
Answer
A
20. A straight line L at a distance of 4 units from the origin makes positive intercepts on the coordinate axes and the perpendicular from the origin to this line makes an angle of 60° with the line x + y = 0. Then, an equation of the line L is
(a) x + √3 y = 8
(b) (√3 + 1) x + ( √3 – 1)y = 8√2
(c) √3 x + y = 8
(d) ( √3 – 1)x + ( 3 + 1)y = 8√2
Answer
D
21. Let f (x) = 5 -|x – 2|and g(x) =|x + 1|, x ∈R. If f (x) attains maximum value at a and g(x) attains minimum value
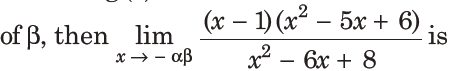
(a) 1/2
(b) – 3 /2
(c) – 1/ 2
(d) 3/2 D
Answer
A
22. Let a∈R and the three vectors
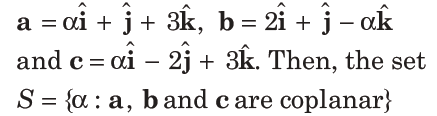
(a) is singleton
(b) is empty
(c) contains exactly two positive numbers
(d) contains exactly two numbers only one of which is positive
Answer
B
23. A person throws two fair dice. He wins `R.s. 15 for throwing a doublet (same numbers on the two dice), wins R.s. 12 when the throw results in the sum of 9, and loses R.s. 6 for any other outcome on the throw. Then, the expected gain/loss (in R.s.) of the person is
(a)1/2 gain
(b)1/4loss
(c)1/2loss
(d) 2 gain
Answer
C
24. The tangents to the curve y = (x – 2)2-1 at its points of intersection with the line x – y = 3, intersect at the point
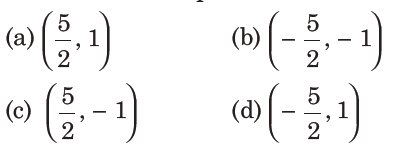
Answer
C
25. If α, β and y are three consecutive terms of a non-constant GP such that the equations ax2+ 2βx +y = 0 and x2 + – 1 = 0 have a common root, then, α(β + y) is equal to
(a) 0
(b) ab
(c) ag
(d) bg
Answer
D
26. Let A, B and C be sets such that Φ ≠ A ∩ B ⊆ C.Then, which of the following statements is not true?
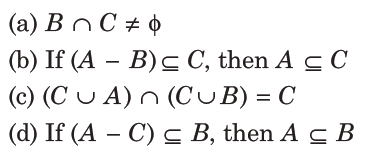
Answer
D
27. The general solution of the differential equation (y2-x3)dx-xydy=0(x≠0) is (where,C is a constant of integration)
(a) y2 -2x2+Cx3 = 0
(b) y2 -2x3+Cx2 = 0
(c) y2 +2x2+Cx3 = 0
(d) y2 -2x3+Cx2 = 0
Answer
B
28. If the area (in sq units) bounded by the parabola y2 = 4λx and the line y = λx, λ> 0, is 1/9 , then λ is equal to
(a) 2 √6
(b) 48
(c) 24
(d) 4 √3
Answer
C
29. The length of the perpendicular drawn from the point (2, 1, 4) to the plane containing the lines
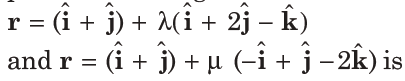
(a) 3
(b)1/3
(c) 3
(d)1/√3
Answer
C
30. The term independent of x in the expansion of
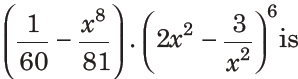
equal to
(a) – 72
(b) 36
(c) – 36
(d) – 108
Answer
C
