Class 12 Mathematics Sample Paper Term 1 Set A
Please see below Class 12 Mathematics Sample Paper Term 1 Set A with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Term 1 Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.
CBSE Sample Paper for Class 12 Mathematics Term 1 Set A
SECTION-A
In this section, attempt any 16 questions out of Questions 1 –20.
Each Question is of 1 mark weightage.
1. What is the principal value branch of sec–1 x ?
(A) (–1, 1)
(B) [–1, 1]
(C) [0,π] , – {π/2}
(D) [0,π]
Answer
C
2. What is the derivative of the function y = xtanx ?
(A) xtanx(xsecx + sec x logx)
(B) x tanx [tanx/x + sec2 logx]
(C) x tanx (2x sec x + tanx log x))
(D) x tanx (tan x/x – sec2 x logx)
Answer
B
3. Matrix A =[aij] m x n is a square matrix if
(A) m > n
(B) m < n
(C) m = 1
(D) m = n
Answer
D
4. Calculate the determinant of the given matrix
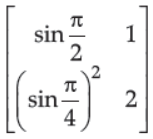
(A) 1/2
(B) -1/2
(C) 3/2
(D) None of the above
Answer
A
5. Absolute maximum of the function 2x + 5 in [5, 10] ?
(A) 5
(B) 10
(C) 20
(D) 25
Answer
D
6. If

(A) –6
(B) –36
(C) 6
(D) 36
Answer
D
7. Given set A = {a, b, c}. An identity relation in set A is:
(A) R= {(a, b), (a, c)}
(B) R= {(a, a), (b, b), (c, c)}
(C) R= {(a, a), (b, b), (c, c), (a, c)}
(D) R= {(c, a), (b, a), (a, a)}
Answer
B
8. For a square matrix A = [aij] the quantity calculated for any element aij in A as the product of (-1)i+j and determinant of the square sub-matrix of order (n-1) obtained by leaving the ith row and jth column of A is known as
(A) Cofactor
(B) Minor
(C) Coefficient
(D) Elements
Answer
A
9. What is the absolute minimum of the function |x – 3| in the interval [4, 5] ?
(A) 2
(B) 4
(C) 6
(D) 8
Answer
A
10. What is the general interval for sine function to become a bijective function?
(A) [nπ – π/2 , nπ + π/2]
(B) [nπ , nπ + π/2]
(C) [-π/2 , nπ + π/2]
(D) [π – π/2 , π+π/2]
Answer
A
11. Let R be relation from R to R the set of real numbers defined by R = {(x, y): x, y Î R and x – y + √3 is an irrational number}. Then, R is:
(A) Reflexive
(B) Transitive
(C) Symmetric
(D) An equivalence relation
Answer
D
12. if x = at4, y = at3 then dy/dx will be
(A) 3/4t
(B) 3/4t2
(C) 3/4
(D) 3t/4
Answer
A
13. Every Identity matrix is a :
(A) Zero matrix
(B) Row matrix
(C) Scalar matrix
(D) Column matrix
Answer
C
14. If y = sin x log x then the value of dy/dx is
(A) sin x log x – 1
(B) sin x/x + cos x log x
(C) cos x/x + sin x log x
(D) 1/x – cos x log x
Answer
B
15. For Matrix A =


Answer
C
16. Which of the following line perpendicular to the tangent to curve y = x2 – 5 at x=1.
(A) 2y+x – 35 = 0
(B) 2x−3y+35 = 0
(C) 4x+7y+35 = 0
(D) 3x+7y+21= 0
Answer
A
17. Calculate the value of x such that the matrix A =

(A) –1, 2
(B) 2, 3
(C) 1
(D) No such value exist
Answer
A
18. If y = √sin x+y , then dy/dx is equal to
(A) cos x/2y-1
(B) cos x/ 1-2y
(C) sin x/1-2y
(D) sin x/2y-1
Answer
A
19. Maximize Z = x + y, subject to x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
(A) the value of z is minimum at every point on line x – y = –1
(B) there is no feasible region with these constraints.
(C) the value of z is minimum at every point on line –x + y = 1
(D) None
Answer
B
20. Which of the following is true for the given function?
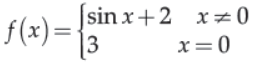
(A) Continuous at x = 0
(B) Not continuous at 0
(C) differentiable at 0
(D) None of the above
Answer
B
SECTION-B
In this section, attempt any 16 questions out of the Questions 21 -40.
Each Question is of 1 mark weightage.
21. Which of the following functions from Z into Z are bijections?
(A) f(x) = x3
(B) f(x) = x + 8
(C) f(x) = 4x + 1
(D) f(x) = x2 + 7
Answer
B
22. If y = log (1-x2/1+x2) , then dy/dx is equal to
(A) 4×3/1-x4
(B) -4x/1-x4
(C) 1/4-x4
(D) -4x3/1-x3
Answer
B
23. The feasible region for an LPP is always a ___________ polygon.
(A) Concave
(B) Convex
(C) Both A and B
(D) None
Answer
B
24. Local maximum of the function 3x4 −20x3 +36x2 +322 in (−10,10) ?
(A) 2
(B) 3
(C) 0
(D) 5
Answer
A
25. If the matrix A is both symmetric and skew symmetric, then
(A) A is a diagonal matrix
(B) A is a zero matrix
(C) A is a square matrix
(D) None of these
Answer
B
26. f(x) = [x] The function is:
(A) Not Continuous
(B) continuous
(C) Differentiable
(D) None of these
Answer
A
27. What is the domain of the sec–1 x ?
(A) [−∞,∞]
(B) (−∞,∞)
(C) (–1, 1)
(D) (−∞,−1]∪[1,∞)
Answer
D
28. If A =

(A) a27
(B) a9
(C) a6
(D) a2
Answer
C
29. The tangent to the curve y = e2x at the point (0, 1) meets x-axis at :
(A) (0, 1)
(B) (-1/2 , 0)
(C) (2, 0)
(D) (0, 2)
Answer
B
30. Consider the set A = {1, 3, 5, 7}. The number of reflexive relations on set A is :
(A) 212
(B) 122
(C) 24
(D) 42
Answer
A
31. The interval on which the function f (x) = 2x3 + 9x2 + 12x -1 is decreasing is :
(A) [–1, ∞)
(B) (–2, –1)
(C) (–∞, –2]
(D) [–1, 1]
Answer
B
32. If A =
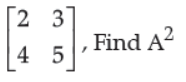

Answer
B
33. A corner point of a feasible region is a point in the region which is the __________ of two boundary lines.
(A) Intersection
(B) Disjoint
(C) Middle point
(D) None
Answer
A
34. The function f(x) = 2x3 – 3x2 – 12x + 4, has
(A) two points of local maximum
(B) two points of local minimum
(C) one maxima and one minima
(D) no maxima or minima
Answer
C
35. If A =

then A2 – 5A + 7I2 is equal to
(A) 0
(B) 1
(C) –1
(D) 2
Answer
A
36. The principal value of tan−1(-√3) is :
(A) π/3
(B) -π/3
(C) 2π/3
(D) π/6
Answer
B
37. The principal value of sec -1(2/√3) is :
(A) π/3
(B) π/2
(C) π/6
(D) π/4
Answer
C
38. Evaluate the determinant Δ =

(A) –17
(B) log318
(C) log28
(D) 15/2
Answer
D
39. The points at which the tangents to the curve y = x3 – 12x + 18 are parallel to x-axis are :
(A) (2, 2), (–2, –34)
(B) (2, 34), (–2, 0)
(C) (0, 34), (–2, 0)
(D) (2, 2), (–2, 34)
Answer
D
40. If matrix A = [1 2 3]. Write A.A’ where A’ is the transpose of matrix A.
(A) 4
(B) 21
(C) 14
(D) 28
Answer
C
SECTION-C
In this section, attempt any 8 questions. Each question is of 1-mark weightage.
Questions 46-50 are based on a Case-Study.
41. Z = 20x1 + 20x2, subject to x1 ≥ 0, x2 ≥ 2, x1 + 2x2 ≥ 8, 3x1 + 2x2 ≥ 15, 5x1 + 2x2 ≥ 20.
The minimum value of Z occurs at :
(A) (8, 0)
(B) (5/2 , 15/4)
(C) (0, 10)
(D) (7/2 , 9/4)
Answer
D
42. Maximum slope of the curve y = –x3 + 3x2 + 9x – 27 is :
(A) 0
(B) 12
(C) 16
(D) 32
Answer
B
43. The curve y = x1/5 has at (0, 0)
(A) a vertical tangent (parallel to y-axis)
(B) a horizontal tangent (parallel to x-axis)
(C) an oblique tangent
(D) no tangent
Answer
A
44. The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y.
Compare the quantity in Column A and Column B

(A) The quantity in column A is greater.
(B) The quantity in column B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined on the basis of the information supplied.
Answer
B
45. Is the value of the determinant

dependent on the value of θ.
(A) Yes
(B) No
(C) None of the above
(D) All of the above
Answer
B
CASE-STUDY
Neha wants to prepare a handmade gift box for her sister’s birthday at home. For making lower part of box; the takes a square piece of card board of side 10 cm.

Based on the given information, answer the following questions.
46. If x cm be the length of the square card board which is to be cut off from corners of the square piece of side 10 cm, the possible value of x will be given by the interval.
(A) [0, 10]
(B) (0, 20)
(C) (0, 5)
(D) None of these
Answer
C
47. Volume of the open box formed by folding up the cutting corner can be expressed as
(A) V = x(10 – 2x)2
(B) V = (x – 10)(10 – 2x)2
(C) V = x(10 – 2x)(10 + 2x)
(D) V = (x – 5)(10 – 2x)2
Answer
A
48. The values of x for which dV/dx = 0 are,
(A) 5/3 ,-2
(B) 5, 5/3
(C) 5 – , 3/2
(D) 5, 3
Answer
B
49. Neha is intrested in maximising the volume of the box. So, what should be the side of the square to be cut off so that the volume of the box is maximum.
(A) 4 cm
(B) 3 cm
(C) 5 cm
(D) 5/3 cm
Answer
C
50. The maximum volume of the box is
(A) 1000/9 cm3
(B) 2000/9 cm3
(C) 2000/27 cm3
(B) 1000/cm3
Answer
C
