Please refer to Chapter 11 Permutations and Combinations MCQ Class 11 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 11 Mathematics. Students should refer to MCQ Questions for Class 11 Mathematics with Answers to score more marks in Grade 11 Mathematics exams. Students should read the chapter Permutations and Combinations and then attempt the following objective questions.

MCQ Questions Class 11 Mathematics Chapter 11 Permutations and Combinations

The Permutations and Combinations MCQ Class 11 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.

Question: The number of words which can be formed out of the letters of the word ARTICLE, so that vowels occupy the even place is 
(a) 1440
(b) 144
(c) 7!
(d)⁴C₄x³C₃ 

Different words are being formed by arranging the letters of the word ‘SUCCESS’. All the words obtained by written in the form of a dictionary.

Question: The rank of the word ‘SUCCESS’ in the dictionary is
(a) 328
(b) 329
(c) 330
(d) 331 

Question: Statement I The number of non-negative integral solutions of

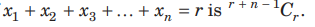
Statement II The number of ways in which n identical things can be distributed into r different groups is ^n+r-1 C _n. A The number of words in which the two C are together but no two S are together, is
(a) 120
(b) 96
(c)24
(d) 420 

Question: The number of words in which the consonants appear in alphabetic order is
(a) 42
(b) 40
(c) 420
(d) 280 

Assertion and Reason
Each of these questions contains two statements : Statement I (Assertion) and Statement II (Reason). Each of these questions also has four alternative choices, only one of which is the correct answer. You have to select one of the codes (a), (b), (c) and (d) given below.
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I.
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I.
(c) Statement I is true; Statement II is false.
(d) Statement I is false; Statement II is true..
Question: Statement I A number of four different digit is formed with the help of the digits 1, 2, 3, 4, 5, 6, 7 in all possible ways. Then, number of ways which are exactly divisible by 4 is 200.
Statement II A number divisible by 4, if unit place digit divisible by 4.   

Question: Statement I The number of different car licence plates can be constructed, if the licences contain three letters of the English alphabet followed by a three digit number is (26)3x (900)  (if repetitions are allowed).
Statement II The number of permutations of n different things taken r at a time when each things may be repeated any number of times is n^r   

Question: Statement I From a group of 8 men and 4 women at team of 5, including atleast one woman can be formed in 736 ways.
Statement II Number of ways of selecting at least one woman from m ^{m +n} C _n–^m C _n   

Question: Statement I Number of rectangle on a chess board is 8C₂x8C_2..
Statement II To form a rectangle we have to select any two of the horizontal line and any two of the vertical line. 

Question: Statement I Product of five consecutive natural numbers is divisible by 4!.
Statement II Product of n consecutive natural numbers is divisible by (n+1)! )

Question: Statement I The sum of the digits in the tens place of all numbers formed with the help of 2, 3, 4, 5 taken all at a time is 84.
Statement II The sum of the digits in the units place of all numbers formed with the help of  a₁,a₂,…,a_n taken all at a time is (n -1)!(a₁+a₂+..+a_n) (repetition of digits is not allowed).

Question: Statement I Number of ways in which 10 identical toys can be distributed among 3 students, if each receives atleast one toys is ⁹C₂.
Statement II Number of positive integral solutions of x+ y+ z+ w = 7 is ⁶C₂ 

Question: Statement I Number of ways in which Indian team (11 players) can bat, if Yuvraj wants to bat before Dhoni and Pathan wants to bat after Dhoni is 11!/3!.
Statement II Yuvraj, Dhoni and Pathan can be arranged in batting order in 3! ways. 

Question:  Statement I The number of ways distributing 10 identical balls in 4 distinct boxes such that no box is empty is ⁹C₃ .
Statement II The number of ways of choosing any 3 places, from 9 different places is ⁹C₃ 

Question:  In a shop there are five types of ice-creams available.
A child buys six ice-creams.
Statement I The number of different ways the child can buy the six ice-creams is ¹⁰C₅.
Statement II The number of different ways the child can buy the six ice-creams is equal to the number of different ways of arranging 6 A’s and 4 B’s in a row. 

Question:  Statement I Let E = { 1,2 ,3 4 }  and F = {a,b}. Then, the number of onto functions from E to F is 14.
Statement II Number of ways in which four distinct objects can be distributed into two different boxes is
14, if no box remains empty.

Question:  Statement I The number of non-negative integral solutions of

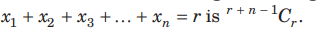
Statement II The number of ways in which n identical things can be distributed into r different groups is ^n+r-1C_n. 

Question: Let T_n be the number of all possible triangles formed by joining vertices of an n-sided regular polygon. If T_n+1-T_n= 10, then the value of n is 
(a) 7
(b) 5
(c) 10
(d) 8 

Question:  Let A B and two sets containing 2 elements and 4 elements respectively. The number of subsets of A B × having 3 or more elements is 
(a) 256
(b) 220
(c) 219
(d) 211   

Question:  Let X = {1 ,2 , 3,4 ,5.} The number of different ordered pairs (Y, Z) that can formed such that Y ⊆ X, Z X ⊆ x and Y ∩ zis empty, is
(a) 5²
(b) 3⁵
(c) 2⁵
(d) 5³ 

Question: Eight chairs are numbered 1 to 8. Two women and 3 men wish to occupy one chair each. First the women choose the chairs from amongst the chairs 1 to 4 and then men select from the remaining chairs.
Find the total number of possible arrangements.
(a) 1440
(b) 1450
(c) 1460
(d) None of these 

Question: The number of different four digit numbers that can be formed with the digits 2, 3, 4, 7 and using each digit only once is 
(a) 120
(b) 96
(c) 24
(d) 100 

Question: If the letters of the word RACHIT are arranged in all possible ways as listed in dictionary. Then, what is the rank of the word RACHIT? 
(a) 479
(b) 480
(c) 481
(d) 482 

Question: How many different non-digit numbers can be formed from the digits of the number 223355888 by rearrangement of the digits so that the odd digits occupy even places?
(a) 16
(b) 36
(c) 60
(d) 180 

Question: How many even numbers of 3 different digits can be formed from the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 (repetition of digits is not allowed)?
(a) 224
(b) 280
(c) 324
(d) None of these 

Question: In how many ways can the letters of the word PERMUTATIONS be arranged, if the words start with P and end with S?
(a) 1814400
(b) 1814405
(c) 1824050
(d) None of these  

Question: Find the number of different words that can be formed from the letters of the word TRIANGLE, so that no vowels are together. 
(a) 14000
(b) 14500
(c) 14400
(d) 14402   

Question: The number of 5-digits telephone numbers having atleast one of their digits repeated, is
(a) 90000
(b) 100000
(c) 30240
(d) 69760   

Question: We are to form different words with the letters of the word INTEGER. Let m1 be the number of words in which I and N are never together and m2 be the number of words which begin with I and end with R, then m₁/m₂  is equal to
(a) 30
(b) 60
(c) 90
(d) 180   

Question: If the letters of the word KRISNA are arranged in all possible ways and these words are written out as in a dictionary, then the rank of the word KRISNA is
(a) 324
(b) 341
(c) 359
(d) None of these

Question: The sum of the digits in unit place of all the numbers formed with the help of 3, 4, 5 and 6 taken all at a time is
(a) 432
(b) 108
(c) 36
(d) 18   

Question: Find the number of permutations of n distinct things taken r together, in which 3 particular things must occur together.

Question: There are 10 persons named P₁,p₂,p₃,…p₁₀· Out of 10 persons, 5 persons are to be arranged in a line such that in each arrangement P₁ must occur whereas P₄ and P₅ do not occur. Find the number of such possible arrangements.
(a) 4210
(b) 4200
(c) 4203
(d) 4205 

Question: If the letters of the word MOTHER are written in all possible orders and these words are written out as in a dictionary, then the rank of the word MOTHER is 
(a) 240
(b) 261
(c) 308
(d) 309 

Question: In a circus there are ten cages for accommodating ten animals. Out of these four cages are so small that five out of 10 animals cannot enter into them. In how many ways will it be possible to accommodate ten animals in these ten cages?
(a) 66400
(b) 86400
(c) 96400
(d) None of these 

Question: The total number of permutations of n (>1) different things taken not more than r at a time, when each thing may be repeated any number of times is 
(a) n(nⁿ-1)/n-1
(b) n^r-1/n-1
(c) n(n^r-1)/n-1 
(d) None of these 

Question: If a denotes the number of permutations of x + 2 things taken all at a time, b the number of permutations of x things taken 11 at a time and c the number of permutations of x − 11 things taken all at a time such that a = 182 bc, then the value of x is
(a) 15
(b) 12
(c) 10
(d) 18 

Question: The number of ways in which seven persons can be arranged at a round table, if two particular persons may not sit together is
(a) 480
(b) 120
(c) 80
(d) None of these 

Question: The number of ways in which 10 candidates A₁, A₂,….,  A₁₀  can be ranked such that A₁ is always above A₁₀ is
(a) 5!
(b) 2(5!)
(c) 10!
(d) 1/2(10!) 

Question: 20 persons are invited for a party. In how many different ways can they and the host be seated at circular table, if the two particular persons are to be seated on either side of the host?
(a) 20 !
(b) 2⋅18 !
(c) 18 !
(d) None of these 

Question: In how many ways can 15 members of a council sit along a circular table, when the Secretary is to sit on one side of the Chairman and the Deputy Secretary on the other side?
(a) 2 12 × !
(b) 24
(c) 2x 15 !
(d) None of these 

Question: How many numbers lying between 10 and 1000 can be formed from the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 repetition of digits is allowed) ?
(a) 1024
(b) 810
(c) 2346
(d) None of these 

Question: Let A be a set containing 10 distinct elements. Then, the total number of distinct functions from A to A is
(a) 10!
(b) 10¹⁰
(c) 2¹⁰
(d) 2¹⁰ -1   

Question: In how many ways can 5 boys and 5 girls sit in a circle so that no two boys sit together?
(a) 5! ×5 ! 
(b) 4! x 5!
(c) 5!x 5!/2
(d) None of these 

Question: How many 10-digit numbers can be written by using the digits 1 and 2 ?
(a) 10 C₁+⁹C₂
(b) 2¹⁰
(c) ¹⁰C₂
(d) 10!   

Question: The figures 4, 5, 6, 7, 8 are written in every possible order. The number of numbers greater than 56000 is
(a) 72
(b) 96
(c) 90
(d) 98 

Question: The number of times the digits 3 will be written when listing the integers from 1 to 1000 is 
(a) 269
(b) 300
(c) 271
(d) 302 

Question: If ⁿC₁₂= ⁿC₈ , then n is equal to
(a) 20
(b) 12
(c) 6
(d) 30