Please see below Class 12 Mathematics Sample Paper Term 1 Set E with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Term 1 Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.

CBSE Sample Paper for Class 12 Mathematics Term 1 Set E

Section A

In this section, attempt any 16 questions out of Questions 1-20. Each question is of 1 mark weightage.

1. The domain of (cos^-1x) is
(a) [0, π]
(b) [-1, 1]
(c) [0, 1]
(d) None of these

2. On the set N of all natural numbers, define the relation R by aRb if GCD of a and b is 2.
Then, R is
(a) reflexive but not symmetric
(b) symmetric only
(c) reflexive and transitive
(d) not reflexive, not symmetric, not transitive

3. The solution set of the inequation x + 2y > 4 is
(a) half plane that contains the origin
(b) open half plane not containing the origin
(c) whole xy-plane except the points lying on the line 2x + y = 5
(d) None of the above

4. The function f(x) =

(a) x = 0
(b) x = 1
(c) x = -1
(d) None of these

5. The function f (x) = tan x – x
(a) always increases
(b) always decreases
(c) never increases
(d) sometimes increases and sometimes decreases

6. If A =

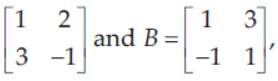
then the value of |A| + | B | is
(a) 28
(b) 7
(c) – 3
(d) 4

7. Minor of an element of a determinant of order n(n ≥ 2) is a determinant of order
(a) n
(b) n – 1
(c) n – 2
(d) n + 1

8. If

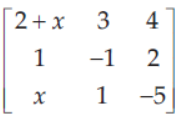
is a singular matrix, then 13x is
(a) – 25
(b) 25
(c) 5
(d) – 5

9. If f (x) = 2x and g(x) = x²/2 + 1 , then which of the following can be a discontinuous function?
(a) f (x) + g (x)
(b) f (x) – g(x)
(c) f (x)× g (x)
(d) g(x)/f(x)

10. If Δ =

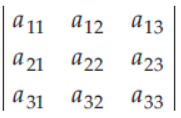
and A_ij is cofactor of a_ij , then value of D is given by
(a) a₁₁ A₃₁ + a₁₂A₃₂ + a₁₃A₃₃
(b) a₁₁A₁₁ + a₁₂A₂₁ + a₁₃A₃₁
(c) a₂₁A₁₁ + a₂₂A₁₂ + a₂₃A₁₃
(d) a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁

11. Corner points of the feasible region for an LPP are : (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5).
Let Z = 2x + 3y the objective function. The minimum value of Z occurs at
(a) (0, 2) only
(b) (3, 0) only
(c) the mid-point of the line segment joining the points (0, 2) and (3, 0) only
(d) any point on the line segment joining the points (0, 2) and (3, 0)

12. The objective function of an LPP is
(a) a constraint
(b) a function to be optimised
(c) a relation between the variables
(d) None of the above

13. If y = a + bx² , and x d²y/dx² = k ,dy/dx , then k is equal to
(a) 0
(b) 5
(c) 1
(d) 2

14. The principal value of cot-1(-√3) is
(a) π/6
(b) -π/6
(c) 5π/6
(d) None of these

15. If A is any square matrix of order 2 x 2 such that |A| = 3, then the value of |adjA| is
(a) 3
(b) 1/3
(c) 9
(d) 27

16. Matrices A and B will be inverse of each other only, if
(a) AB= BA
(b) AB= BA= O
(c) AB= O and BA= I
(d) AB= BA= I

17. If A is matrix of order m x n and B is a matrix such that AB’ and B’A are both defined, then order of matrix B is
(a) m x m
(b) n x n
(c) n x m
(d) m x n

18. If A is a square matrix of order 3, with |A| = 9, then the value of | 3 adjA|
(a) 2187
(b) 81
(c) 8
(d) 324

19. The element a₂₃ of a 3 x 3matrix A = [a_ij], whose elements are given by a_ij = |i2 – j2 |/5 is
(a) 1
(b) 2
(c) 3
(d) 0

20. If A and B are square matrices of the same order, then (A + B) (A – B) is equal to
(a) A² – B² 
(b) A² – BA – AB – B²
(c) A²– B² + BA – AB
(d) A² – BA + B² + AB

Section B

In this section, attempt any 16 questions out of Questions 21-40. Each question is of 1 mark weightage.

21. The interval on which the function f (x) =2x³ + 9x² + 12x – 1 is decreasing, is
(a) [-1, ∞]
(b) [-2, -1]
(c) [-∞, -2]
(d) [- 1, 1]

22. Derivative of cot^-1

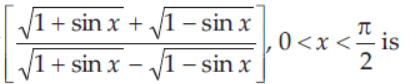
(a) 1/2
(b) 1
(c) 2
(d) None of these

23. The corner points of the feasible region determined by the following system of linear inequalities 2x + y ≤ 10, x + 3y ≤ 15, x , y ≥ 0 are (0 ,0) (5, 0) (3, 4) and (0, 5). Let Z = px + qy , where p , q > 0. Condition on p and q, so that the maximum of Z occurs at both (3, 4) and (0, 5), is
(a) p = q
(b) p = 2q
(c) p = 3 q
(d) q = 3 p

24. Let X be the set of all persons living in Delhi. The persons a and b in set X are said to be related, if the difference in their ages is atmost 4 yr. The relation is
(a) an equivalence relation
(b) reflexive and transitive but not symmetric
(c) symmetric and transitive but not reflexive
(d) reflexive and symmetric but not transitive

25. If A and B are invertible matrices, then which of the following is not correct?
(a) adj A= |A| A^-1
(b) det (A)^-1= [det(A)^-1]
(c) (AB)^-1= B^-1 A^-1
(d) (A+B)^-1 = B^-1+A^-1

26. If area of a triangle is 35 sq units with vertices (2, – 6), (5, 4) and (k, 4), then k is
(a) 12
(b) – 2
(c) – 12, -2
(d) 12, -2

27. The function f (x) = √3 sin 2x + cos 2x + 10 is one-one in the interval
(a) [-π/2 , π/2]
(b) [-π/4 , π/4]
(c) [-π/3 ,π/3]
(d) [-π/3 , π/6]

28. If y = tan-1 (3x-x³/1-3x²) , 1/√3 < x < 1/√3 , then dy/dx is
(a) 3/1+x²
(b) 1/1+x²
(c) -3/1+x²
(d) 3/1-x²

29. Which of the following functions is decreasing on (0 , π/2) ?
(a) sin²x
(b) tan x
(c) cos x
(d) cos³x

30. Let R be set of real numbers. If f : R → R is defined by f (x) = ex , then f is
(a) surjective but not injective
(b) injective but not surjective
(c) bijective
(d) neither surjective nor injective

31. If

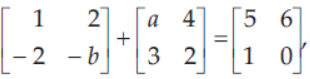
then a² + b² is equal to
(a) 20
(b) 22
(c) 12
(d) 10

32. If y = √3x + 2 + 1/√2x²+ 4 , then dy/dx is equal to

33. If y = sin x and z = cos x, then dy/dz at x = π/4 is equal to
(a) 1
(b) – 1
(c) 0
(d) 2

34. If x + y = K is normal to y² = 12x , then K is
(a) 3
(b) 9
(c) – 9
(d) – 3

35. If A, B are symmetric matrices of same order, then AB – BA is a
(a) skew-symmetric matrix
(b) symmetric matrix
(c) zero matrix
(d) identity matrix

36. Let X be the set of all citizens of India. Elements x, y in X are said to be related, if the difference of their age is 5 yr. Which one of the following is correct?
(a) The relation is an equivalence relation on X
(b) The relation is symmetric but neither reflexive nor transitive
(c) The relation is reflexive but neither symmetric nor transitive
(d) None of the above

37. If Z = x – 2y be the objective function and min Z = -10. The minimum value occurs at point
(a) (14, 2)
(b) (2/3 , 16/3)
(c) (2, 3)
(d) (0, 0)

38. Solve the linear programming problem, minimise Z = 2x – 3y subject to the constraints 2x + 3y ≤ 20, x – y ≤ 10 and x ≥ 0, y ≥ 0.
(a) Z = 0
(b) Z = -10
(c) Z = -20
(d) Z = 20

39. sin (π/3 – sin^-1(-1/2)) is equal to
(a) 1/2
(b) 1/3
(c) 1/4
(d) 1

40. If A =

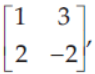
then A-1 equals

Section C

In this section, attempt any 8 questions. Each question is of 1 mark weightage. Questions 46-50 are based on Case-Study.

41. The derivative of cos-1(2x-1) w.r.t. cos-1 x is
(a) 2
(b) -1/2√1-x²
(c) 2/x
(d) 1 – x²

42. The points at which the tangents to the curve y = x³ – 12x + 18 are parallel to X-axis are
(a) (2, – 2) and(- 2, – 34)
(b) (2, 34) and(- 2, 0)
(c) (0, 34) and(- 2,0)
(d) (2, 2) and(- 2, 34)

43. Let f(x) =

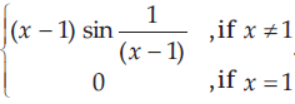
Then, which of the following is true?
(a) f (x) is not differentiable at x = 1
(b) f (x) is differentiable at x = 1
(c) cannot say
(d) None of the above

44. If y = (tan^-1 x²) , then the value of (x²+1)² y² + 2x(x²+1) y₁ is
(a) 2
(b) 3
(c) 4
(d) None of these

45. If x = ex/y , then dy/dx is equal to
(a) x-y/x log x
(b) y-x/log x
(c) y-x/x log x
(d) x-y/log x

CASE STUDY

In a college, an architecture design a auditorium for its cultural activities purpose. The shape of the floor of the auditorium is rectangular and it has a fixed perimeter, say P.

Based on the above information, answer the following questions.

46. If l and b represents the length and breadth of the rectangular region, then relation between the variable is :
(a) l + b = P
(b) l² + b² = p²
(c) 2(l + b) = P
(d) l +2b = P

47. The area (A) of the floor, as a function of l can be expressed as
(a) A = Pl + l/2
(b) A = Pl + l²/2
(c) A = Pl – 2l²/2
(d) A = l2/2 + pl²

48. College manager is interested in maximising the area of floor ‘A’. For this purpose, the value of lmust be
(a) p/4
(b) p/3
(c) p/2
(d) P

49. The value of b, for which the area of floor is maximum, is
(a) p/16
(b) p/4
(c) P/3
(d) p/2

50. Maximum area of floor is
(a) p²/64
(b) p²/28
(c) p²/16
(d) p²/4