Mathematical Reasoning MCQ Class 11 Mathematics
Please refer to Chapter 14 Mathematical Reasoning MCQ Class 11 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 11 Mathematics. Students should refer to MCQ Questions for Class 11 Mathematics with Answers to score more marks in Grade 11 Mathematics exams. Students should read the chapter Mathematical Reasoning and then attempt the following objective questions.
MCQ Questions Class 11 Mathematics Chapter 14 Mathematical Reasoning
The Mathematical Reasoning MCQ Class 11 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question: If p, q r and are simple propositions with truth value true, false and true respectively, then the truth value of ((~p ν q ) ∧~r) ⇒ p
(a) true
(b) false
(c) true, if r is false
(d) true, if q is true
Answer
A
Question: If p = He is intelligent.
q = He is strong.
Then, symbolic form of statement ‘‘It is wrong that he is intelligent or strong,’’ is
(a) ~ p ν~ p
(b) ~ (p ∧ q)
(c) ~ (p ν q )
(d) p v ~ q
Answer
C
Question: Let p and q be two statements. Then, p ν q is false, if
(a) p is false and q is true
(b) both p and q are false
(c) both p and q are true
(d) None of these
Answer
B
Question: In the truth table for the statement (~ p→ ~q ) (~q⇒ ~ p), the last column has the truth value in the following order
(a) TTTF
(b) FTTF
(c) TFFT
(d) TTTT
Answer
C
Question: If p: A man is happy.
q: A man is rich.
Then, the statement, “If a man is not happy, then he is not rich” is written as
(a) ~ p → ~ q
(b) ~ q → p
(c) ~ q → ~ p
(d) q → p ~ p
Answer
A
Question: Which of the following is the inverse of the proposition “If a number is a prime, then it is odd.”
(a) If a number is not a prime, then it is odd
(b) If a number is not a prime, then it is not odd
(c) If a number is not odd then it is not a prime
(d) If a number is not odd, then it is a prime
Answer
B
Question: If p ⇒ (q ν r) is false, then the truth values of p, q, r are respectively,
(a) T, F, F
(b) F, F, F
(c) F, T, T
(d) T, T, F
Answer
A
Question: The false statement in the following is

Answer
B
Question: Let
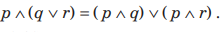
Then, this law is known as
(a) Commutative law
(b) Associative law
(c) De Morgan’s law
(d) Distributive law
Answer
D
Question:
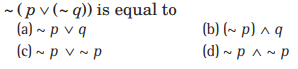
Answer
B
Question: (~ (~p )) ∧ q is equal to
(a) ~ p ν ∧ q
(b) p ∧ q
(c) p ∧ ~ q
(d) ~ p ∧ ~ q
Answer
B
Question: For the following three statements
p:2 is an even number
q :2 is a prime number.
r : Sum of two prime numbers is always even, then the symbolic statement(p ∧ q) → ~ r means
(a) 2 is an even and prime number and the sum of two prime numbers is always even
(b) 2 is an even and prime number and the sum of two prime numbers is not always even
(c) 2 is an even and prime number, then the sum of two prime numbers is not always even
(d) 2 is an even and prime number, then the sum of two prime numbers is always even
Answer
C
Question: Let p be the proposition Mathematics is interesting and let q be the proposition that Mathematics is difficult, then the symbol p ∧ q means
(a) Mathematics is interesting implies that Mathematics is difficult.
(b) Mathematics is interesting implies and is implied by Mathematics is difficult.
(c) Mathematics is interesting and Mathematics is difficult.
(d) Mathematics is interesting or Mathematics is difficult.
Answer
C
Question: For two statements p and q p: A quadrilateral is a parallelogram, q : The opposite sides are parallel.
Then, the compound proposition, “A quadrilateral is a parallelogram if and only if the opposite sides are parallel” is represented by
(a) p ν q
(b) p→ q
(c) p ∧ q
(d) p ↔ q
Answer
D
Question: If p q and are two statements such that p: the questions paper is easy p : the questions paper is easy q: we shall pass, then the symbolic statement ~p → p ~ q means
(a) If the question paper is easy, then we shall pass
(b) If the question paper is not easy, then we shall not pass
(c) The question paper is easy and we shall pass
(d) The question paper is easy or we shall pass
Answer
B
Question: If p, q, r and s are four simple statements, such as
p: The school bus will come
q : I go to school
r : I shall meet my friends
s : I shall go out for a movie, then the compound statement, “If the school bus does not come or I will not go to school, then I shall meet my friend and go out for a movie.” is represented by
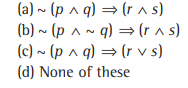
Answer
A
Question: Which of the following is true for the statements p and q?
(a) p ∧ q is true when at least one of p and q is true
(b) p → q is true when p is true and q is false
(c) p ↔ q is true only when both p q and are true
(d) ~ (p ν q) is false only when both p q and are false
Answer
D
Question: p ν q is true when
(a) both p and q are true
(b) p is true and q is false
(c) p is false and q is true
(d) All of these
Answer
D
Question: Which of the following is true?
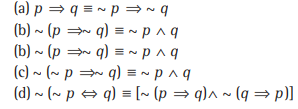
Answer
C
Question: The statement (~p ∧ q) ν ~ is
(a) p ν q
(b) p ∧ q
(c) ~ (p ν q)
(d) ~ (p ∧ q)
Answer
D
Question: Negation of the statement p →(q ∧r ) is

Answer
D
Question: ~ [{~ p) ∧ q] is equal to
(a) p ν (~ q)
(b) p ν q
(c) ~ (p ν q)
(d) ~(p ∧ q)
Answer
A
Question: If statements p and r are false and q is true, then truth value of ~ p ⇒ (q ∧ r) ν is r is
(a) T
(b) F
(c) either T or F
(d) neither T nor F
Answer
B
Question: Which of the following is always true?
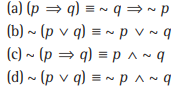
Answer
C
Question: If p and q are simple propositions, then p ⇒ ∼ q is true when
(a) both p q and are true
(b) both p q and are false
(c) p is false and q is true
(d) None of these
Answer
C
Question: The statement p ⇒(q⇒ p) is equivalent to
(a) p ⇒ (p ⇒q)
(b) p ⇒(p ν q)
(c) p ⇒(p ∧ q)
(d) p ⇒ (p⇔ q)
Answer
B
Question: Let truth values of p be F and q be T. Then, truth value of ~ (~ p ν q) is
(a) T
(b) F
(c) either T or F
(d) neither T nor F
Answer
B
Question: Which of the following is logically equivalent to

Answer
D
Question: If p, q, are true statements and r s, are false statements, then the truth value of ~ ((p ∧ ~r )v (~q v s )) is
(a) true
(b) false
(c) false for any p
(d) None of these
Answer
B
Question: ~ (p ν q) ν (~ p ∧ q) is logically equivalent to
(a) ~ p
(b) p
(c) q
(d) ~ q
Answer
A
Question: Which of the following is equivalent to (p ∧ q)?
(a) p → ~ q
(b) ~ (~ p ∧ ~ q)
(c) ~ ( p → ~ q)
(d) None of these
Answer
B
Question: If the compound statement p →( ~p v q ) is false, then the truth value of p q and are respectively
(a) T, T,
(b) T, F
(c) F, T
(d) F, F
Answer
B
Question:

Answer
D
Question: The negation of the compound statement (p v q) ∧ r is
(a) (~ p v ~ q) ∧ ~ r
(b) (~p ∧ ~ q) v ~ r
(c) ~ ( p v q) ⇒ r
(d) p ∧ q
Answer
B
Question: The negation of (p v q) ) ∧ ( p v~ r) is
(a) (~ p ∧ ~ q) v (p v ~ r)
(b) (~ p ∧ ~ q) ∧ (~p ∧ r)
(c) (~ p ∧ ~ q) v (~ p ∧ r)
(d) None of these
Answer
B
We hope you liked the above Mathematical Reasoning MCQ Class 11 Mathematics. In case you have any questions please put them in the comments box below and our teachers will provide you a response.
