Conic Sections MCQ Class 11 Mathematics
Please refer to Chapter 11 Conic Sections MCQ Class 11 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 11 Mathematics. Students should refer to MCQ Questions for Class 11 Mathematics with Answers to score more marks in Grade 11 Mathematics exams. Students should read the chapter Conic Sections and then attempt the following objective questions.
MCQ Questions Class 11 Mathematics Chapter 11 Conic Sections
The Conic Sections MCQ Class 11 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. The tangent drawn at any point P to the parabola y2 = 4ax meets the directrix at the point K, then the angle which KP subtends at its focus is
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer
D
Question: If the lines 3x-4y-7=0 and 2x-3y-5=0 are two diameters of a circle of area 49π sq units, the equation of the circle is
(a) x2+ y2+ 2x- 2y- 62=0
(b) x2+ y2– 2x + 2y- 62=0
(c) x2+ y2 -2x + 2y-47=0
(d) x2+ y2 + 2x- 2y-47=0
Answer
C
Question: If the pair of lines ax2+ 2(a+b) xy+by2= 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector, then
(a) 3a2+2ab+3b2=0
(b) 3a2+10ab+3b2=0
(c) 3a2-2ab+3b2=0
(d) 3a2-10ab+3b2=0
Answer
A
Question: Let C be the circle with centre (0, 0) and radius 3. The equation of the locus of the mid-points of the chords of the circleC that subtend an angle 2π/3 at its centre is
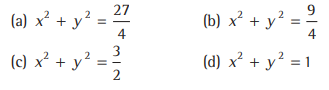
Answer
B
Question: A circle touches the x-axis and also touches the circle with centre at (0, 3) and radius 2. The locus of the centre of the circle is
(a) a parabola
(b) a hyperbola
(c) a circle
(d) an ellipse
Answer
A
Question: The smallest circle with centre on y-axis and passing through the point (7, 3) has radius
(a) √58
(b) 7
(c) 3
(d) 4
Answer
B
Question: If the lines 2x+3y+1=0 and 3x-y-4=0 along diameters of a circle of circumference 10π, then the equation of the circle is
(a) x2 + y2 -2x +2y -23=0
(b) x2 + y2 -2x +2y -23=0
(c) x2 + y2 -2x +2y -23=0
(d) x2 + y2 +2x -2y -23=0
Answer
A
Question: The intercept on the line y=x by the circle x2+y2-2x=0 is AB. Equation of the circle on AB as a diameter is
(a) x2 +y2 – x- y =0
(b) x2 +y2 – x +y=0
(c) x2 +y2 + x +y=0
(d) x2 +y2 +x -y=0
Answer
A
Question: If a circle passes through the point(a ,b) and cuts the circle x2+y2 = 4 orthogonally, then the locus of its centre is
(a) 2ax+2by+(a2+b2+4) =0
(b) 2ax+2by+(a2+b2+4) =0
(c) 2ax- 2by+(a2+b2+4) =0
(d) 2ax- 2by- (a2+b2+4) =0
Answer
B
Question: A variable circle passes through the fixed point A(p, q) and touches x-axis. The locus of the other end of the diameter through A is
(a) (x-p)2=4gy
(b) (x-q)2=4py)
(c) (y-p)2=4qx
(d) (y-q)2=4px
Answer
A
Question: 41. If the circles x2+ y2 +2ax +cy +a= 0 and x2 +y2 -3ax +dy-1=0 intersect in two distinct points P and Q, then the line 5 0 x by a + − = passes through P and Q for
(a) no value of a
(b) exactly one value of a
(c) exactly two values of a
(d) infinitely many values of a
Answer
A
Question: How many common tangents can be drawn to the following circles x2+y2= 6 and x2+y2+6x+2y+1=0 ?
(a) 4
(b) 3
(c) 2
(d) 1
Answer
A
Question: The line 3x-2y=k meets the circle x2+ y2=4r2 at only one point, if k2
(a) 20r2
(b) 52/9 r2
(c) 52/9r2
(d) 20/9r2
Answer
B
Question: If the line 3x-4y-k=0,(k>0) touches the circle x2+y2-4x-8y-5=0 at (a ,b ) then k+ a+ b is equal to
(a) 20
(b) 22
(c) −30
(d) −28
Answer
A
Question: Find the equation of the circle which passes through the points (2, 3) and (4, 5) and the centre lies on the straight line y-4X+3=0 .
(a) x2+ y2 – 4x – 10y +25= 0
(b) x2 +y2 -4x -10y – 25= 0
(c) x2 +y2 -4x+ 10y -25= 0
(d) None of the above
Answer
A
Question: If the line x /a+y/ b=1 moves such that 1/a2+1/b2=1/c2‘ where c is a constant, then the locus of the foot of the perpendicular from the origin to the line is
(a) straight line
(b) circle
(c) parabola
(d) ellipse
Answer
B
Question: A line through P(1 , 4) intersect a circle x2+y2=16 at A B and , then A and B,then pA·PB is equal to
(a) 1
(b) 2
(c) 3
(d) 4
Answer
A
Question: A line through (0, 0) cuts the circle x2+y2-2ax=0 at A B and , then locus of the centre of the circle drawn AB as diameter is
(a) x2+ y2– 2ay =0
(b) x2+y2+ay=0
(c) x2+ y2+ ax =0
(d) x2+y2-ax=0
Answer
D
Question: The equation of the tangents to the circle x2+y2=4,which are parallel to x y + + = 2 3 0, are
(a) x-2y=2
(b) x +2y= ±2√3
(c) x+2y= ± 2 √5
(d) x- 2y = ± 2√5
Answer
C
Question:
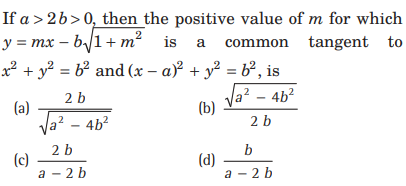
Answer
A
Question: If a circle passes through the point of intersection of the coordinate axes with the lines λx-y +1=0 and x -2y + 3 0, then the value of λ is
(a) 2
(b) 4
(c) 6
(d) 3
Answer
A
Question: The square of the length of the tangent from (3,-4) to the circle x2+y2-4x-6y+3=0 is
(a) 20
(b) 30
(c) 40
(d) 50
Answer
C
Question: The length of the tangent drawn from any point on
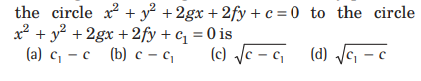
Answer
D
Question: The tangent at (1,7) to the curve x2= y- 6 touches the circle x2+y2+16x+12y+c=0 at
(a) (6, 7)
(b) (- 6,7 )
(c) ( 6,7)
(d) (-6,7)
Answer
D
Question: The normal at the point (3, 4) on a circle cuts the circle at the point (–1, –2). Then, the equation of the circle is
(a) x2+ y2+ 2x-2y -13 =0
(b) x2 +y2– 2x-2y -11 =0
(c) x2+ y2 -2x +2y +12 =0
(d) x2 +y2 -2x -2y +14 =0
Answer
B
Question: Centre of circle whose normals are x2-2xy-3x+6y=0 is
(a) (3,3/2)
(b) (3,3/2)
(c) (3/2,3)
(d) None of these
Answer
A
Question: If line ax by + = 0 touches x2+y2+2x+4y=0 and is a normal to the circle x2+y2-4x+2y-3=0, then value of (a ,b ) will be
(a) (2,1)
(b) (1, –2)
(c) (1, 2)
(d) (–1, 2)
Answer
C
Question. If the tangents at P and Q on the parabola meet in T, then SP, ST and SQ are in
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
B
Question. AB, AC are tangents to a parabola y2 = 4ax; p1 ,p2 , p3 are the lengths of the perpendiculars from A, B,C on any tangent to the curve, then p1 ,p2 , p3 are in
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
B
Question. The length of the chord of the parabola y2 = x which is bisected at the point (2, 1) is
(a) 2√3
(b) 4√3
(c) 3√2
(d) 2√5
Answer
D
Question. The DPQR of area A is inscribed in the parabola y2 = 4ax such that the vertex P lies at the vertex of the parabola and the base QR is a focal chord. The modules of the difference of the ordinates of the points Q and R is
(a) A/2a
(b) A/a
(c) 2A/a
(d) 4A/a
Answer
C
Question. On the parabola y = x2, the point atleast distance from the straight line y = 2x – 4 is
(a) (1, 1)
(b) (1, 0)
(c) (1, -1)
(d) (0, 0)
Answer
A
Question. If the equation of parabola is x2 = – 9y , then equation of directrix and length of latusrectum are
(a) y = -9/4 ,8
(b) x = 9/4 ,9
(c) y = -9/4 ,8
(d) None of these
Answer
C
Question. Consider the following statements
I. The equation of the parabola whose focus is at the origin is y2 = 4ax.
II. The line lx + my + n = 0 will touch the parabola
y2 = 4ax , if ln = am2.
Which of these is/are correct ?
(a) Only (I)
(b) Only (II)
(c) Both of these
(d) None of these
Answer
C
Question. The number of distinct normals that can be drawn to parabola y2 = 16x from the point (2, 0), is
(a) 1
(b) 2
(c) 3
(d) 0
Answer
A
Question. The length of the chord of the parabola x2 = 4y passing through the vertex and having slope cota is
(a) 4 cosa cosec2a
(b) 4 tana sec a
(c) 4 sin a sec2a
(d) None of these
Answer
A
Question. If the vertex of the parabola is the point (– 3, 0) and the directrix is the line x + 5 = 0, then its equation is
(a) y2 = 8(x+ 3)
(b) x2 = 8(y+ 3)
(c) y2 = – 8(x+ 3)
(d) y2 = 8(x+ 5)
Answer
A
Question. The arithmetic mean of the ordinates of the feet of the normals from (3, 5) to the parabola y2 = 8x is
(a) 4
(b) 0
(c) 8
(d) None of these
Answer
B
Question. The line x – 1 = 0 is the directrix of the parabola y2 – kx + 8 = 0. Then, one of the value of k is
(a) 1/8
(b) 8
(c) 4
(d) 1/4
Answer
C
Question. If the focus of a parabola is (0, – 3) and its directrix is y = 3 and its equation is
(a) x2 = – 12y
(b) x2 = 12y
(c) y2 = – 12x
(d) y2= 12x
Answer
A
Question. If two different tangents of y2 = 4ax are the normals to x2 = 4by , then
(a) |b|>1/2√2
(b) |b|<1/2√2
(c) |b |> 1/√2
(d) |b |< 1/√2
Answer
B
Question. Equation of chord of the parabola y2 = 16 whose mid-point is (1, 1), is
(a) x + y = 2
(b) x – y = 0
(c) 8x + y = 9
(d) 8x – y = 7
Answer
D
Question. The chord AB of the parabola y2 = 4ax cuts the axis of the parabola at C. If A = (at12 , 2at1 ) B = (at22 , 2at2 ) and AC: AB= 1:3, then
(a) t2 = 2t1
(b) t2 + 2t1 = 0
(c) t1 + 2t2 = 0
(d) None of these
Answer
B
Question. AB is a chord of the parabola x2 = 4ax with vertex A, BC is drawn perpendicular to ABmeeting the axis atC. The projection of BC on the axis of the parabola is
(a) a
(b) 2a
(c) 4a
(d) 8a
Answer
C
Question. The focal chord to y2 = 16 is tangent to (x – 6)2 + y2 = 2 , then the possible values of the slope of this chord are
(a) {-1,1}
(b) {-2,2}
(c) {-2,1/2}
(d) {2,-1/2}
Answer
A
Question. Let P be the point (1, 0) and Q a point on the locus y2 = 8x . The locus of mid-point of PQ is
(a) x2 – 4y + 2 = 0
(b) x2 – 4y + 2 = 0
(c) y2 + 4y + 2 = 0
(d) y2 – 4y + 2 = 0
Answer
D
Question. If a parabolic reflector is 20 cm in diameter and 5 cm deep, then the focus is
(a) (0, 5)
(b) (5, 0)
(c) (0, -5)
(d) (-5, 0)
Answer
B
Question. Find the area of the triangle formed by the lines joining the vertex of the parabola x2 = 12 to the ends of its latusrectum.
(a) 19 sq units
(b) 18 sq units
(c) 20 sq units
(d) 17 sq units
Answer
B
Question. Find the length of the line segment joining the vertex of the parabola y2 = 4ax and a point on the parabola where the line segment makes an angle q to the x-axis.
(a) 2a cosΘ /sin2Θ
(b) 4a cosΘ /sin2Θ
(c) 4a cosΘ /3sin2Θ
(d) None of these
Answer
B
Question. If a ¹ 0 and the line 2bx + 3cy + 4d = 0 passes through the points of intersection of the parabolas y2 = 4ax and x2 = 4ay , then
(a) d2 + (2b + 3c)2 = 0
(b) d2 + (3b + 2c)2 = 0
(c) d2 + (2b – 3c)2 = 0
(d) d2 + (3b+ 2c)2 = 0
Answer
A
Question. The circle x2 + y2 + 2λx = 0, λ∈R, touches the parabola y2 = 4x externally. Then,
(a) λ> 0
(b) λ < 0
(c) λ > 1
(d) None of these
Answer
A
Question. The shortest distance between the parabolas y2 = 4x and y2 = 6x is
(a) 2
(b) √5
(c) 3
(d) None of these
Answer
B
Question. A parabola is drawn with focus at (3, 4) and vertex at the focus of the parabola y2 – 12x – 4y + 4 = 0. The equation of the parabola is
(a) x2 – 6x – 8y + 25 = 0
(b) y2 – 8x – 6 + 25 = 0
(c) x2 – 6x + 8y – 25 = 0
(d) x2 – 6x – 8y – 25 = 0
Answer
A
Question. The normal to the parabola y2 = 8x at the point (2, 4) meets the parabola again at the point
(a) (-18, -12)
(b) (-18,12)
(c) (18, 12)
(d) (18, -12)
Answer
D
Question. Three distinct normals to the parabola y2 = x are drawn through a point (c,0), then
(a) c = 1/4
(b) c = 1/2
(c) c > 1/2
(d) None of these
Answer
C
Question. If y1 , y2 , y3 , and are the ordinates of the vertices of a triangle inscribed in the parabola y2 = 4ax , then its area is
(a) 1/2a (y1 – y2)(y2-y3)(y3– y1)
(b) 1/4a (y1 – y2)(y2-y3)(y3– y1)
(c) 1/8a (y1 – y2)(y2-y3)(y3– y1)
(d) None of the above
Answer
C
Question. The locus of a point on the variable parabola y2 = 4ax , whose distance from focus is always equal to k, is equal to (a is parameter)
(a) 4x2 + y2 – 4kx = 0
(b) x2 + y2 – 4kx = 0
(c) 2x2 + 4y2 – 8kx = 0
(d) 4x2 – y2 + 4kx = 0
Answer
A
Question. The radius of circle when a attains its maximum value
(a) 1/√10
(b) 1/√5
(c) 1
(d) 5
Answer
B
Question. The slope of the tangent when radius of the circle is maximum is
(a) 1
(b) 1
(c) 0
(d) 2
Answer
C
Question. The equation of the parabola whose focus is the point (0, 0) and the tangent at the vertex is x – y + 1 = 0 is
(a) x2 + y2 – 2xy – 4x – 4y – 4 = 0
(b) x2 + y2 – 2xy + 4x – 4y – 4 = 0
(c) x2 + y2 – 2xy – 4x + 4y – 4 = 0
(d) x2 + y2 – 2xy – 4x + 4y – 4 = 0
Answer
C
Question. Axis of a parabola is y = x and vertex and focus are at a distance 2 and 2 √2 respectively from the origin. Then, equation of the parabola is
(a) (x – y )2 = 8(x + y – 2)
(b) (x – y )2 = 2(x + y – 2)
(c) (x – y )2 = 4(x + y – 2)
(d) (x + y )2 =2(x – y + 2)
Answer
A
Question. The minimum area bounded by the tangent and the coordinate axes is
(a) 1
(b) 1/3
(c) 1/2
(d) 1/4
Answer
D
Directions (Q. Nos. 14-18) Each of these questions contains two statements : Statement I (Assertion) and Statement II (Reason). Each of these questions also has four alternative choices, only one of which is the correct answer. You have to select one of the codes (a), (b), (c) and (d) given below.
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I.
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I.
(c) Statement I is true; Statement II is false.
(d) Statement I is false; Statement II is true.
Question. Statement I If normal at the ends of double ordinate x = 4 of parabola y2 = 4x meet the curve again at P and P¢ respectively, then PP’ = 12 units.
Statement II If normal at t1 of y ax 2 = 4 meet the parabola again at t2, then t2 = t1 -2/t1
Answer
C
Question. Statement I The lines from the vertex to the two extremities of a focal chord of the parabola y2 = 4ax are at an angle of π/2
Statement II If extremities of focal chord of parabola are (at12 ,2at1 ) and (at22 , 2at2) , then t1t2 = – 1.
Answer
B
Question. Statement I The latusrectum of a parabola is 4 units, axis is the line 3x + 4 y – 4 = 0 and the tangent at the vertex is the line 4x – 3 y + 7 = 0, then the equation of directrix of the parabola is 4x – 3 y + 8 = 0.
Statement II If P be any point on the parabola and let PM and PN are perpendiculars from P on the axis and tangent at the vertex respectively, then (PM)2 = (latusrectum) (PN)
Answer
D
Question. Statement I Slope of tangents drawn from (4, 10) to parabola y2 = 9x are 1/4,9/4
Statement II Two tangents can be drawn to parabola from any point lying outside parabola.
Answer
B
Question. Statement I In parabola y ax 2 = 4 , the circle drawn taking focal radii as diameter touches y-axis.
Statement II The portion of the tangent intercepted between point of contact and directrix subtends 90° angle at focus.
Answer
B
Question. If two tangents drawn from a point P to the parabola y2 = 9x are at right angles, then the locus of P is
(a) x = 1
(b) 2x + 1 = 0
(c) x = -1
(d) 2x – 1 = 0
Answer
C
Question. A parabola has the origin as its focus and the line x = 2 as the directrix. Then, the vertex of the parabola is at
(a) (2, 0)
(b) (0, 2)
(c) (1, 0)
(d) (0, 1)
Answer
C
Question. The equation of the tangent to the parabola y2 = 8x is y = x + 2. The point on this line from which the other tangent to the parabola is perpendicular to the given tangent is
(a) (0, 2)
(b) (2, 4)
(c) (-2, 0)
(d) (-1, 1)
Answer
C
Question. Let P be a point whose coordinates differ by unity and the point does not lie on any of the axes of reference. If the parabola y2 = 4x + 1 passes through P, then the ordinate of P may be
(a) 3
(b) -1
(c) 5
(d) 1
Answer
(A,C)
Question. Parabola y2 = 4x and the circle having it’s centre at (6, 5) intersect at right angle. Possible point of intersection of these curves can be
(a) (9, 6)
(b) (2,√8)
(c) (4, 4)
(d) (3, 2√3)
Answer
(a,c)
Question. If the normals at two points P and Q of a parabola y2 = 4ax intersect at a third point R on the curve, then the product of ordinates of P and Q is
(a) 4a2
(b) 2a2
(c) – 4a2
(d) 8a2
Answer
D
Question. If the tangent and normal at any point P of a parabola meet the axes in T andG respectively, then
(a) ST ¹ SG = SP
(b) ST – SG ¹ SP
(c) ST = SG = SP
(d) ST = SG × SP
Answer
C
Question. The locus of the vertices of the family of parabolas y = a2 x2 /3 + a2 x/2 – 2a is
(a) xy = 35/36
(b) xy = 64/105
(c) xy = 105/64
(d) xy = 3/4
Answer
C
Question. If tangents at A and B on the parabola y2 = 4 intersect at pointC, then ordinates of A,C and Bare
(a) always in AP
(b) always in GP
(c) always in HP
(d) None of these
Answer
A
Question. The number of real tangents that can be drawn to the curve y2 + 2xy + x2 + 3y + 1 = 0 from the point (1, – 2) is
(a) one
(b) two
(c) zero
(d) None of these
Answer
C

We hope you liked the above Conic Sections MCQ Class 11 Mathematics. In case you have any questions please put them in the comments box below and our teachers will provide you a response.

