Permutations and Combinations Class 11 Mathematics Important Questions
Please refer to Permutations and Combinations Class 11 Mathematics Important Questions with answers below. These solved questions for Chapter 7 Permutations and Combinations in NCERT Book for Class 11 Mathematics have been prepared based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these solved problems properly as these will help them to get better marks in your class tests and examinations. You will also be able to understand how to write answers properly. Revise these questions and answers regularly. We have provided Notes for Class 11 Mathematics for all chapters in your textbooks.
Important Questions Class 11 Mathematics Chapter 7 Permutations and Combinations
Question. There are 6 students A, B, C, D, E, F.
(i) In how many ways can they be seated in a line so that C and D do not sit together?
(ii) In how many ways can a committee of 4 be formed so as to always include C?
(iii) In how many ways can a committee of 4 be formed so as to always include C but exclude E?
Answer : (i) 480 (ii) 10 (iii) 4
Question. (i) There are n stations on a railway line. The number of kinds of tickets printed (no return tickets) is 105. Find the number of stations.
(ii) Twelve persons meet in a room and each shakes hand with all others. Find the number of hand- shakes.
Answer : (i) 15 (ii) 66
Question. There are 7 men and 3 ladies contesting for two vacancies; an elector can vote for any number of candidates not exceeding the number of vacancies. In how many ways can he vote?
Answer : 55
Question. A party of 6 is to be formed from 10 boys and 7 girls so as to include 3 boys and 3 girls. In how many different ways can the party be formed if two particular girls refuse to join the same party?
Answer : 3600
Question. Given, n–1Cr : nCr : n+1Cr = 6 : 9 : 13. Find n and r.
Answer : n = 12
Question. If nPr = 2520 and nCr = 21, find r.
Answer : 5
Question. Find the number of sides of a polygon having 44 diagonals.
Answer : n = 11
Question. We wish to select 6 persons from 8 persons, but if the persons A is chosen, then B must be chosen. In how many ways can the selection be made?
Answer : 22
Question. In how many ways, 50 different things can be distributed among 5 person so that three of them get 12 things each and two get 7 things each.
Answer : [ 50! / ( (12!)3 .(7!)2 .3! ) ] . 5!
Question. Six “X” s (crosses) have to be placed in the squares of the figure given below, such that each row contains at least one X. In how many different ways can this be done?
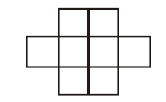
Answer : 26
Question. Out of 6 gentlemen and 4 ladies a committee of 5 is to be formed. In how many ways can this be done so as to include at least one lady in each committee?
Answer : 246
Question. Find the number of zeroes in 100!
Answer : 24
Question. There are 15 gates to enter a city from north and 10 gates to enter the city from east. In how many ways a person can enter the city?
Answer : 25
Question. In how many ways 5 different red balls, 3 different black balls and 2 different white balls can be arranged along a row?
Answer : 10 !
Question. There are 6 single choice questions in an examination. How many sequence of answers are possible, if the first three questions have 4 choices each and the next three have 5 each?
Answer : 8000
Question. Three tourists want to stay in five different hotels. In how many ways can they do so if :
(a) each hotel can not accommodate more than one tourist?
(b) each hotel can accommodate any number of tourist?
Answer : (a) 60 (b) 125
Question. (a) How many words can be formed using letters of the word EQUATION taken all at a time?
(b) How many of these begin with E and end with N?
(c) How many of these end and begin with a consonants?
(d) In how many of these vowels occupy the first, third, fourth, sixth and seventh positions?
Answer : (a) 40320 (b) 720 (c) 4320 (d) 720
Question. In how many ways can six persons be arranged in a row?
Answer : 720
Question. How many 5-digit odd numbers can be formed using digits 0, 1, 2, 3, 4, 5 without repeating digits?
Answer : 288
Question. Find number of different 4 letter words can be formed using the letters of the word ‘HISTORY’.
Answer : 840
Question. A city has 12 gates, In how many ways can a person enter the city through one gate and come out through a different gate?
Answer : 132
Question. In how many ways 5 different red balls, 3 different black balls and 2 different white balls can be placed in 3 different boxes such that each box contains only 1 ball.
Answer : 720
Question. Five person entered the lift cabin on the ground floor of an 8-floor house. Suppose each of them can leave the cabin independently at any floor beginning with the first. Find the total number of ways in which each of the five persons can leave the cabin
(i) at any one of the 7 floors (ii) at different floors
Answer : (i) 75 (ii) 2520
Question. How many 5-digits numbers divisible by 4 can be formed using digits 0, 1, 2, 3, 4, 5, without repetition of digits.
Answer : 144
Question. How many six-digit numbers divisible by 25 can be formed using digits 0, 1, 2, 3, 4, 5?
Answer : 42
Question. If 18Cr = 18Cr+2, find rC5.
Answer : 56
Question. Determine n, if 2nC3 : nC3 = 11 : 1.
Answer : n = 6
Question. A committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of (i) exactly 3 girls (ii) at least 3 girls
Answer : (i) 504 (ii) 588
Question. A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if the team has
(i) no girls ? (ii) at least one boy and one girl? (iii) at least three girls?
Answer : (i) 21 (ii) 441 (iii) 91
Question. Determine the number of 5 card combinations out of a deck of 52 cards if at least one of the 5 cards has to be a king?
Answer : 886656
Question. A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected from the lot.
Answer : 200
Question. A committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of at most 3 girls?
Answer : 1632
Question. A sports team of 11 students is to be constituted, choosing at least 5 from class XI and at least 5 from class XII. If there are 25 students in each of these classes, in how many ways can the teams be consitituted?
Answer : 2.25 C .25 C
Question. There are ten points in a plane. Of these ten points, four points are in a straight line and with the exception of these four points, no three points are in the same straight line. Find
(i) the number of triangles formed
(ii) the number of straight lines formed.
(iii) the number of quadrilaterals formed, by joining these ten points.
Answer : (i) 116 (ii) 40 (iii) 185
Question. How many different teams of 7 players can be chosen from 10 players?
Answer : 120
Question. If nCr–1 = 36, nCr = 84 and nCr+1 = 126, find n and r.
Answer : n = 9, r = 3
Question. Find the number of triangles which can be formed having vertices at angular points of a convex polygon of m sides.
Answer : mC3
Question. Sudha wants to choose any 9 stamps from a set of 11 different stamps. How many diferent selections can she make?
Answer : 55
Question. There are 4 oranges 5 apples and 6 mangoes in a fruit basket. In how many ways can a person make a selection of fruits from among the fruits in the basket?
Answer : 209
Question. In an examination a minimum is to be secured in each of 5 subjects for a pass. In how many ways can a student fail?
Answer : 31
Question. Five balls of different colours are to be placed in three boxes of different size. Each box can hold all five balls. In how many different ways can we place the balls so that no box remains empty.
Answer : 150
Question. To fill 12 vacancies there are 25 candidates of which 5 are from scheduled castes. If 3 of the vacancies are reserved for scheduled caste candidates while the rest are open to all, find the number of ways in which the selections can be made.
Answer : 5C3 × 20C9 + 5C4 × 20C8 + 5C5 × 20C7
Question. In how many ways can a committee be selected from 15 persons if the committee is to have
(i) 3 members, (ii) 13 members
Answer : (i) 455 (ii) 105
Question. How many lines can be drawn through 21 points on a circle?
Answer : 210
Question. There are 12 seats in the first row of a theater of which 4 are to be occupied. Find the number of ways of arranging 4 persons so that:
(i) no two persons sit side by side.
(ii) each person has exactly one neighbour.
Answer : (i) 3024 (ii) 864
Question. Create two fair dice which when rolled together have an equal probability of getting any sum from 1 to 12.
Answer : {1, 2, 3, 4, 5, 6}; {0, 0, 0, 6, 6, 6}
Question. How many seven-letters words can be formed by using the letter of the word SUCCESS so that:
(i) the two C are together but not two S are together?
(ii) no two C and no two S are together?
Answer : (i) 24 (ii) 96
Question. In how many ways can a pack of 52 cards be
(i) distributed equally among four players in order?
(ii) divided into 4 groups of 13 cards each?
(iii) divided into four sets of ’20, 15, 10, 7 cards?
(iv) divided into four sets, three of them having 15 cards each and the fourth having 7 cards?
Answer : (i) 52! / (13!)4 (ii) 52! / 4!(13!)4 (iii) 52! / 20!15!10!7! (iv) 52! / (15!)3 3! 7!
Question. A train is going from Cambridge to London stops at nine intermediate station. Six persons enter the train during the journey with six different tickets. How many different sets of tickets they have had ?
Answer : 8145060
Question. Find the number of polynomials of the form x3 + ax2 + bx + c which are divisible by x2+ l and where a, b, c belong to {1, 2,…, n}.
Answer : ‘n’
Question. You have n objects, each of weight w. When they are weighed in pairs, the sum of the weights of all the possible pairs is 120. When they are weighed in triplets, the sum of the weights of all possible triplets is 480. Find n.
Answer : 10
Question. A boat’s crew consists of 8 men, 3 of whom can only row on one side and 2 only on the other. Find the number of ways in which the crew can be arranged.
Answer : 1728
Question. Find the number of all whole numbers formed on the screen of a calculator which can be recog- nized as numbers with (unique) correct digits when they are read inverted. The greatest number formed on its screen is 999999.
Answer : 100843
Question. How many three digit numbers are of the form xyz with x < y; z < y and x≠ 0.
Answer : 240
Question. (i) A committee consisting of 2 men and 2 women is to be chosen from 5 men and 6 women. In how many ways can this be done?
(ii) A committee of 3 persons is to be constituted from a group of 2 men and 3 women. In how many ways can this be done? How many of these committees would consist of 1 man and 2 women?
Answer : (i) 150 (ii) 10; 6
Question. A bookshelf contains 7 different Mathematics textbooks and 5 different physics textbooks. How many groups of 3 Mathematics and 3 Physics textbooks can be selected?
Answer : 350
Question. Seven points lie on a circle. How many chords can be drawn by joining these points?
Answer : 21
Question. If nC8 = nC6, determine n and hence nC2 .
Answer : n = 14; nC2 = 91
Question. Find n, if nC6 : n–3C3 = 33 : 4.
Answer : n = 11
Question. How many selections of 4 books can be made from 8 different books?
Answer : 70
Question. Out of 7 men and 4 ladies a committee of 5 is to be formed. In how many ways can this be done so as to include at least 3 ladies?
Answer : 91
Question. A candidate is required to answer six out of ten questions which are divided into two groups, each containing five questions and he is not permitted to attempt more than 4 from any group. In how many ways can he make up his choice?
Answer : 200
Question. In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 courses are compulsory for every student?
Answer : 35
Question. How many quadrilaterals can be formed joining the vertices of a convex polygon of n sides?
Answer : nC4
Question. There are 10 professors and 20 students out of whom a committee of 2 professors and 3 students is to be formed. Find in how many ways these committee can be formed if
(i) a particular professor is included?
(ii) a particular professor is excluded ?
Answer : (i) 1C1 × 9C1 × 20C3 (ii) 9C2 × 20C3
Question. From 6 boys and 7 girls a committee of 5 is to be formed so as to include at least one girl. Find the number of ways in which this can be done.
Answer : 7C1 × 6C4 + 7C2 × 6C3 + 7C3 × 6C2 + 7C4 × 6C1 + 7C5 × 6C0 or 12C5 – 6C5
Question. A man has 7 friends and he wants to invite 3 of them at a party. Find how many parties to each of 3 different friends he can give and how many times any particular friend will attend the parties?
Answer : 35; 15
Question. A delegation of 6 members is to be sent abroad out of 12 members. In how many ways can the selection be made so that
(i) A particular member is included ? (ii) A particular member is excluded?
Answer : (i) 462 (ii) 462
