Trigonometric Functions MCQ Class 11 Mathematics
Please refer to Chapter 3 Trigonometric Functions MCQ Class 11 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 11 Mathematics. Students should refer to MCQ Questions for Class 11 Mathematics with Answers to score more marks in Grade 11 Mathematics exams. Students should read the chapter Relations and Functions and then attempt the following objective questions.
MCQ Questions Class 11 Mathematics Chapter 3 Trigonometric Functions
The Trigonometric Functions MCQ Class 11 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. The value of sec2θ + cosec2q is equal to
(a) tan2θ + cot2θ
(b) sec2θ cosec2θ
(c) secθ cosecθ
(d) sin2θ cos2θ
Answer
B
Question:

Answer
A
Question: If in two circles, arcs of the same length subtend angles of 60° and 75° at the centre, find the ratio of their radii.
(a) 4 : 5
(b) 5 : 4
(c) 6 : 5
(d) 5 : 6
Answer
B
Question: Find the length of an arc of a circle of radius 5 cm subtending a central angle measuring 15°.
(a) 5π/13 cm
(b) 5π/12 cm
(c) 7π/12 cm
(d) None of these
Answer
B
Question: Find the degree measure corresponding to the radian 11/16.
(a) 39°22′ 32″
(b) 39° 22′ 30″
(c) 39° 23′ 33″
(d) None of these
Answer
B
Question:

Answer
B
Question: The value of the expression
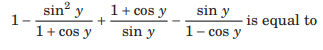
(a) 0
(b) 1
(c) sin y
(d cos y
Answer
D
Question: If f (x ) = cos2 x+sec2x, then
(a) f(x ) < 1
(b) f(x) = 1
(c) 2<f(x)<1
(d) f (x)≥ 2
Answer
D
Question: If sin θ + =cosec θ= 2, then sin2θ + cosec 2θ is equal to
(a) 1
(b) 4
(c) 2
(d) None of these
Answer
D
Question: Which of the following number is rational ?
(a) sin15°
(b) cos15°
(c) sin 15cos 15°
(d) sin 15cos 75°
Answer
C
Question. The angles of a triangle are in A.P. and the ratio of angle in degrees of the least to the angle in radians of the greatest is 60 : p, find the angles in degrees.
(a) 30°, 60°, 90°
(b) 40°, 60°, 90°
(c) 30°, 30°, 120°
(d) 20°, 130°, 30°
Answer
A
Question. The value of 4sina sin (α + π/3) sin (α + 2π/3) =
(a) sin3 α
(b) sin2 α
(c) sin α
(d) sin2 α
Answer
A
Question. Find x from the equation cosec (90° + q) + x cosq cot (90° + q) = sin(90° + q).
(a) cot θ
(b) tan θ
(c) – tan θ
(d) – cot θ
Answer
B
Question. If cosq = -3/5 and p < θ < 3π/2 , then the value of cosecθ + cotθ/secθ – tanθ is
(a) 1/6
(b) 1/7
(c) 1/5
(d) 1/2
Answer
A
Question. If a and b lie between 0 and π/4 , find tan 2a, given that cos(α + β) = 4/5 and sin (α – β) = 5/13 .
(a) 50/33
(b) 56/33
(c) 52/33
(d) 48/33
Answer
B
Question. Find the value of tan(a + b), given that cota = 1/2 , α ∈ (π,3/2 π) and sec β = -5/3 , β ∈ (π/2 , π)
(a) 1/11
(b) 2/11
(c) 5/11
(d) 3/11
Answer
B
Question. A wheel rotates making 20 revolutions per second. If the radius of the wheelis 35 cm, what linear distance does a point of its rim travel in three minutes? (Take p = 22/7)
(a) 7.92 km
(b) 7.70 km
(c) 7.80 km
(d) 7.85 km
Answer
A
Question. Find the angle in radian through which a pendulum swings it its length is 75 cm and tip describes an arc of length 21 cm.
(a) 7/25
(b) 6/25
(c) 8/25
(d) 3/25
Answer
A
Question. The circular measures of two angles of a triangle are 1/2 and 1/3 find the third angle in English system.
(a) 130°15′20′′
(b) 132°15′20′′
(c) 132°16′22′′
(d) 122°16′44′′
Answer
C
Question. The value of 4sina sin (α +π/3) sin (α + 2π/3) =
(a) sin3 α
(b) sin2 α
(c) sin α
(d) sin2 α
Answer
A
Question. Convert 6 radians into degree measure.
(a) 343°38′11′′
(b) 348°33′11′′
(c) 433°38′11′′
(d) 343°37′12′′
Answer
A
Question. If sinA = 3/5 and A is in first quadrant, then the values of sin2A, cos2A and tan2A are
(a) 24/25, 7/25, 24/7
(b) 1/25, 7/25, 1/7
(c) 24/25, 1/25, 24/7
(d) 1/25, 24/25, 1/24
Answer
A
Question. If tanq = 3 and q lies in III quadrant, then find the value of sinq.
(a) 1/√10
(b) 2/√10
(c) -3/√10
(d) -5/√10
Answer
C
Question. Find the radian measure of 520°.
(a) 13π/9
(b) 26π/9
(c) 17π/9
(d) 6π/9
Answer
B
Question. Find the value of sin(40° + q) cos(10° + q) – cos(40° + q) sin(10° + q).
(a) 1/2
(b) 1/4
(c) 1
(d) 0
Answer
A
Question. Find the degree measure of (π/9)c and (-π/3)c
(a) 20°, –60°
(b) 30°, 60°
(c) 20°, 40°
(d) 40°, 50°
Answer
A
Question. If sinA/sinB = m and cosA/cosB = n, then find the value of tan B; n2 < 1 < m2.
(a) n2
(b) ± √1 – n2/m2 – 1
(c) n2/(m2 – 1)
(d) m2
Answer
B
Question. Evaluate 2 cos (22,1/2)°. cos(67,1/2) .
(a) 2
(b) 2
(c) 1/√2
(d) 0
Answer
C
Question. The large hand of a clock is 42 cm long. How much distance does its extremity move in 20 minutes?
(a) 88 cm
(b) 80 cm
(c) 75 cm
(d) 77 cm
Answer
A
Question. Find the value of sin20° sin40° sin80°.
(a) √3/8
(b) √3/2
(c) √3/4
(d) √3
Answer
A
Question. If 3 sinq + 5 cosq = 4, then find the value of 5 sinq – 3 cosq.
(a) ±3 √2
(b) ±5 √2
(c) ± √2
(d) ±7 √2
Answer
A
Question. Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm as shown in figure. [Use π =22/7]
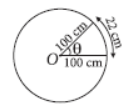
(a) 12°30′
(b) 12°36′
(c) 11°36′
(d) 11°12′
Answer
B
Question. If x sin π/4 cos2 π/3 = tan2(π 3) cosec(π/6)/sec(π /4) )cot2(π /6) , then x =
(a) 2
(b) 4
(c) 8
(d) 16
Answer
C
Question. The value of 3(sinx – cosx)4 + 6(sinx + cosx)2 + 4(sin6x + cos6x) =
(a) 11
(b) 12
(c) 13
(d) 14
Answer
C
Question. If sinq = 3sin(q + 2a), then the value of tan(q + a) + 2tana is
(a) 3
(b) 2
(c) –1
(d) 0
Answer
D
Question. Find the degree measure corresponding to π/32 rad.
(a) 5°37′30′′
(b) 5°30′20′′
(c) 4°30′30′′
(d) 4°20′20′′
Answer
A
Question. Find the radius of the circle in which a central angle of 60° intercepts an arc of length 37.4 cm (Use π = 22/7)
(a) 37.5 cm
(b) 32.8 cm
(c) 35.7 cm
(d) 34.5 cm
Answer
C
Question. If cos x = 4/5 , where x ∈[0, π/2], then the value of cos (x/2) is equal to
(a) 1/10
(b) 2/5
(c) 3/√10
(d) −2/5
Answer
C
Question. If tanq = -4/3 , then sinq is
(a) -4/5 but not 4/5
(b) -4/5 or 4/5
(c) 4/5 but not -4/5
(d) -3/4 or 3/4
Answer
B
Question. The value of √3 cosec 20° – sec 20° is
(a) 1
(b) 7
(c) 2
(d) 4
Answer
D
Question. If tanA + cotA = 4, then tan4A + cot4A is equal to
(a) 110
(b) 191
(c) 80
(d) 194
Answer
D
Question. Express 50° 37′ 30′′ in radian.
(a) 7π/32
(b) 5π/32
(c) 9π/32
(d) π/32
Answer
C
Question. If x sin3q + y cos3q = sinq cosq and x sinq = y cosq, then x2 + y2 is equal to
(a) 2
(b) 0
(c) 3
(d) 1
Answer
D
Question. If sinA – 6 cosA = √7 cosA, then cosA + √6 sinA is equal to
(a) √6 sinA
(b) √7 sinA
(c) √6 cos A
(d) √7 cos A
Answer
B
Question. If A + B = 5π/4, then value of (1 + tan A)(1 + tan B) equals
(a) 1
(b) 2
(c) –2
(d) –1
Answer
B
Question: If tan x +cot x=2, then sin 2n x+cos2n x is equal to
(a) 2n
(b) -1/2
(c) 1/2
(d) None of these
Answer
D
Question: If m sin θ = n sin (θ +2α), then tan (θ +α) cot α is equal to
(a) (m+n) (m-n)
(b) m- n/m+ n
(c) m+n/m -n
(d) 2(m+n )(m-n)
Answer
C
Question:

(a) n = 6
(b) n = 1,2,3,…, 8
(c) n = 5
(d) None of these
Answer
A
Question: If sin A- sin C/cos C -cos A = cot B, then A, B and C , are in
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
A
Question:
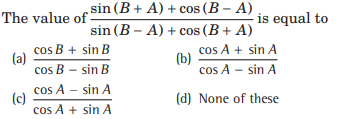
Answer
B
Question: The value of 1- tan2 15°/1+tan2 15° is
(a) 1
(b) 3
(c) 3
(d) 2
Answer
C
Question: If cos (α+β, =4/5 ,sin (α -β) = 5/13 and α, β, lies between 0 and π/4 , then tan 2α is equal to
(a) 16/63
(b) 56/33
(c) 28/33
(d) None of these
Answer
B
Question: The value of(cos A + cos B/sin A- sin B)n + (sin A + sin B/ cos A – cos B)n (where, n is an even) is
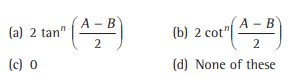
Answer
B
Question: If tan θ = 1/2 and tan Φ = 1/3, then the value of θ +Φ is
(a) π/6
(b) π
(c) 0
(d) π/4
Answer
D
Question: If cos x+ cos y+ cos α = 0 and sin x sin y +sin α = 0, then cot ( x+y/2) is equal to
(a) sin α
(b) cos α
(c) cot α
(d) sin (x+y/2)
Answer
C
Question. The value of 3 tan610° – 27 tan410° + 33 tan210° equals
(a) 0
(b) –1
(c) 1
(d) None of these
Answer
C
Question. Find the value of 2cos45° sin15°.
(a) √3 + 1/2
(b) 1/2
(c) √3 – 1/2
(d) √3/2
Answer
C
Question. If cot x = 4/3 and x lies in third quadrant, then find the value of sec x.
(a) 1/4
(b) 7/4
(c) 2/4
(d) –5/4
Answer
D
ASSERTION – REASON TYPE QUESTIONS
(a) Assertion is correct, reason is correct; reason is a correct explanation for assertion.
(b) Assertion is correct, reason is correct; reason is not a correct explanation for assertion
(c) Assertion is correct, reason is incorrect
(d) Assertion is incorrect, reason is correct.
Question. Assertion : The solution of the equation
tan θ + tan(θ+ π/3) + tan(θ+ 2π/3) = 3
is θ = nπ/3 + π/12, n ∈ I.
Reason : If tan θ = tan α, then θ = nπ + α, n ∈ I.
Answer
A
Question. Assertion : Area of unit circle is π unit2.
Reason : Radian measure of 40° 20′ is equal to l2lπ/ 540 radian.
Answer
B
Question. Assertion : cos(π + x).cos (–x)/sin(π – x).cos(π/2 + x)= cot2 x
Reason : cos (π + θ) = –cos θ and cos (–θ) = cos θ.
Also, sin (π – θ) = sin θ and sin (–θ) = –sin θ.
Answer
A
Question. Assertion : The ratio of the radii of two circles at the centres of which two equal arcs subtend angles of 30° and 70° is 21 : 10.
Reason : Number of radians in an angle subtended at the centre of a circle by an arc is equal to the ratio of the length of the arc to the radius of the circle.
Answer
D
Question. Assertion : The measure of rotation of a given ray about its initial point is called an angle.
Reason : The point of rotation is called a vertex.
Answer
B
Question. Assertion : The second hand rotates through an angle of 180° in a minute.
Reason : The unit of measurement is degree in sexagesimal system.
Answer
D
Question. Assertion : The degree measure corresponding to (–2) radian is –114° 19 min.
Reason : The degree measure of a given radian measure
= 180/π × Radian measure.
Answer
D
Question. Assertion : In a unit circle, radius of circle is 1 unit.
Reason : 1 min (or 1′) is divided into 60s.
Answer
B
Question. Assertion: cosec x is negative in third and fourth quadrants.
Reason : cot x decreases from 0 to – ∞ in first quadrant and increases from 0 to ∞ in third quadrant.
Answer
C
Question. Assertion : If tan(π/2 sinθ) = cot(π/2 cosθ), then sin θ + cos θ = ± √2.
Reason : – √2 ≤ sin θ + cos θ ≤ √2.
Answer
D
Question. Assertion : If tan 2x = –cot (x+π/3) , then x = nπ + 5π/6 ,n ∈ Z.
Reason : tan x = tan y ⇒ x = nπ + y, where n ∈ Z.
Answer
A
We hope you liked the above Relations and Functions MCQ Class 11 Mathematics. In case you have any questions please put them in the comments box below and our teachers will provide you a response.
