Binomial Theorem MCQ Class 11 Mathematics
Please refer to Chapter 8 Binomial Theorem MCQ Class 11 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 11 Mathematics. Students should refer to MCQ Questions for Class 11 Mathematics with Answers to score more marks in Grade 11 Mathematics exams. Students should read the chapter Binomial Theorem and then attempt the following objective questions.
MCQ Questions Class 11 Mathematics Chapter 8 Binomial Theorem
The Binomial Theorem MCQ Class 11 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question: If the last term in the binomial expansion of
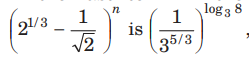
then the 5th term from the beginning is
(a) 210
(b) 420
(c) 105
(d) None of these
Answer
A
Question:

Answer
C
Question: If x2 k occurs in the expansion of +1/X2)n-3
(a) n – 2 k is a multiple of 2
(b) n k – 2 is a multiple of 3
(c) k = 0
(d) None of the above
Answer
B
Question: The coefficient of the term independent of x in the expansion of (1+x+2x3)(3/2x2-1/3x)9 is
(a) 1/3
(b) 19/54
(c) 17/54
(d) 1/4
Answer
C
Question: If the term free from x in the expansion of (√x-k/x2)10 is 405, then the value of k is
(a) ± 1
(b) ± 2
(c) ± 3
(d) ± 4
Answer
C
Question: The coefficient of x in the expansion of(1-3x+7x2)(1-x)16
(a) 19
(b) – 19
(c) 18
(d) – 18
Answer
B
Question: The term independent of x in the expansion of (3x-2/x2)15 is
(a) – 3003 (310)(25)
(b) – 3003 (310)(24)
(c) 3003 (310)(25)
(d) None of these
Answer
A
Question:
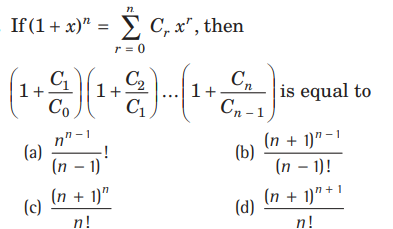
Answer
C
Question:
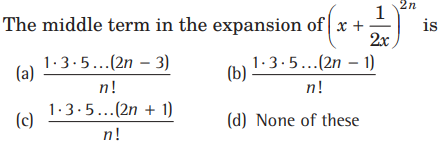
Answer
B
Question: If the middle term of (1/x+xsinx)10 is equal to 7 7/8, then value of x is
(a) 2nπ+π/6
(b) nπ+π/6
(c) nπ+(-1)nπ/6
(d) nπ+(-1)nπ/3
Answer
C
Question: If p is a real number and if the middle term in the expansion of (p/2+2)8 1120, then the value of p is
(a) ± 3
(b) ± 1
(c) ± 2
(d) None of these
Answer
C
Question: If n is even, then the middle term in the expansion of
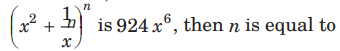
(a) 10
(b) 12
(c) 14
(d) None of these
Answer
B
Question: The largest term in the expansion of (3 +2x) 50 , where
x =1/5 is
(a) 5th
(b) 3th
(c) 7th
(d) 6th
Answer
C
Question: If the sum of the coefficients in the expansion of (x-2y+3z)n is 128, then the greatest coefficient in the expansion of (1 + x)n is
(a) 35
(b) 20
(c) 10
(d) None of the above
Answer
A
Question: The greatest value of the term independent of x, as α varies over R, in the expansion of (xcos α+sinα/x)20is
(a) 20C10
(b) 20C15
(c) 20C19
(d) None of these
Answer
D
Question:
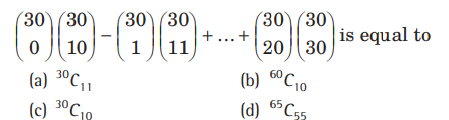
Answer
C
Question: The interval in which x must lie, so that the greatest term in the expansion of (1+x)2n has the greatest coefficient, is
(a) (n-1/n,n/n-1)
(b) (n/n+1,n+1/n)
(c) (n/n+2,n+2/n)
(d) None of these
Answer
B
Question:
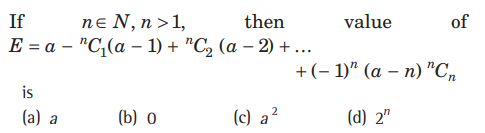
Answer
B
Question:
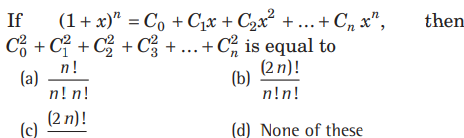
Answer
B
Question: C1/C0+2C2/C1+3C3/C2…+…+15C15/C14 is equal to
(a) 100
(b) 120
(c) –120
(d) None of these
Answer
B
Question:
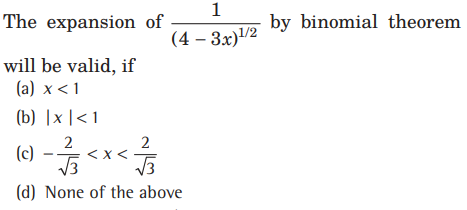
Answer
D
Question:
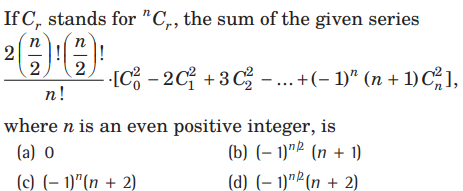
Answer
D
Question: If n is odd, then
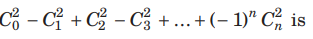
is equal to
(a) 0
(b) 1
(c) ∞
(d) n!/(n/2)2!
Answer
A
Question:
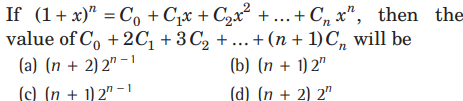
Answer
A
Question:
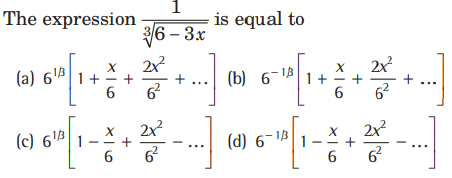
Answer
B
Question: If n>(8+3√7)10,n∈N, ( ) then the least value of n is
(a) (8+3√7)10-(8-3√7) 10
(b) (8+3√7)10-(8-3√7) 10
(c) (8+3√7)10-(8-3√7) 10+1
(d)(8+3√7)10-(8-3√7) 10-1
Answer
B
Question: Let R=(2+√3)2n and f = R – [R ], where [ ·] denotes the greatest integer function, then R (1-f ) is equal to
(a) 1
(b) 2 2n-1
(c) 22n-1
(d) 2nCn
Answer
A
Question: If ar is the coefficient of xr, in the expansion of ( 1+x+x2)n,) then a1-2a2+3a3-…-2na2n … is equal to
(a) 0
(b) n
(c) – n
(d) 2 n a
Question:
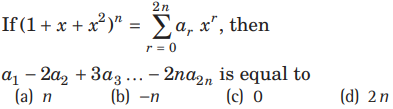
Answer
B
Question: If (1+x)15=C0+C1x+C2X2+…+C15x15, then C2+2C3+3C4+…+14C15 … is equal to
(a) 14 ·2 14
(b) 13· 214 +1
(c) 13 2 1 14× –
(d) None of these
Answer
B
Question:
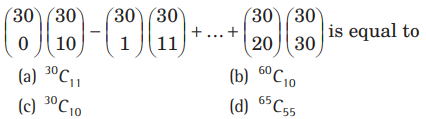
Answer
D
Question:
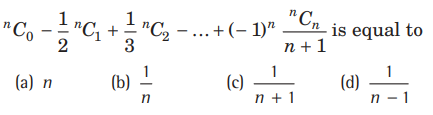
Answer
C
Question: If a and d are two complex numbers, then the sum to (n + 1) terms of the following series aC0-(a+d) C1+(a+2d)C2-…+… is
(a) a/2n
(b) na
(c) 0
(d) None of these
Answer
C
Question: 49n+16n-1 is divisible by
(a) 3
(b) 19
(c) 64
(d) 29
Answer
C
Question: If A = 10001000 and B =(1001) 999, then
(a) A >B
(b) A B =
(c) A< B
(d) None of these
Answer
A
Question:
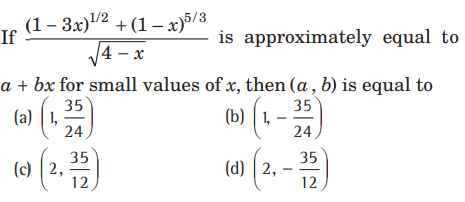
Answer
B
Question: Cube root of 217 is
(a) 6.01
(b) 6.04
(c) 6.02
(d) None of these
Answer
A
Question: If the value of x is so small that x2 and greater powers can be neglected, then
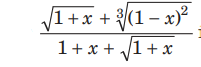
is equal to
(a) 1+5/6x
(b) 1-5/6x
(c) 1+2/3x
(d) 1-2/3x
Answer
B
Question:

Answer
D
We hope you liked the above Binomial Theorem MCQ Class 11 Mathematics. In case you have any questions please put them in the comments box below and our teachers will provide you a response.
