Please refer to Chapter 16 Probability MCQ Class 11 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 11 Mathematics. Students should refer to MCQ Questions for Class 11 Mathematics with Answers to score more marks in Grade 11 Mathematics exams. Students should read the chapter Probability and then attempt the following objective questions.

MCQ Questions Class 11 Mathematics Chapter 16 Probability

The Probability MCQ Class 11 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.

Question. A bag contains 10 balls, out of which 4 balls are white and the others are non-white. The probability of getting a non-white ball is
(a) 2/5
(b) 3/5
(c) 1/2
(d) 2/3

Question. The probability that a card drawn from a pack of 52 cards will be a diamond or king is:
(a) 1/52
(b) 2/13
(c) 4/13
(d) 1/13

Question. A die is thrown. Then, match the events of column-I with their respective sample points in column-II.

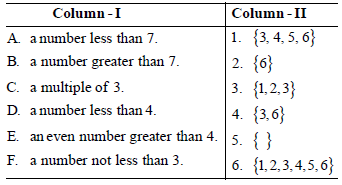
Codes
     A B C D E F
(a) 6 5 4 3 2 1
(b) 1 2 3 4 5 6
(c) 5 6 4 3 2 1
(d) 3 4 5 6 2 1

Question. While shuffling a pack of 52 playing cards, 2 are accidentally dropped. The probability that the missing cards to be of different colours is
(a) 29/52
(b) 1/2 
(c) 26/51
(d) 27/51

Question. The dice are thrown together. The probability of getting the sum of digits as a multiple of 4 is:
(a) 1/9
(b) 1/3
(c) 1/4
(d) 5/9

Question. Probability of an event can be
(a) – 0.7
(b) 11/9
(c) 1.001
(d) 0.6

Question. If a single letter is selected at random from the word ‘PROBABILITY’, then the probability that it is a vowel, is
(a) 1/3
(b) 4/11
(c) 2/11
(d) 3/11

Question. In a non-leap year, the probability of having 53 Tuesday or 53 Wednesday is
(a) 1/7
(b) 2/7
(c) 3/7
(d) None of these

Question. A letter is chosen at random from the word ‘ASSASSINATION’. Then, the probability that letter is (i) a vowel (ii) a consonant, respectively are
(a) 6/13 and 6/13
(b) 7/13 and 6/13
(c) 6/13 and 7/13
(d) 7/13 and 7/13

Question. A coin is tossed twice. Then, the probability that atleast one tail occurs is
(a) 1/4
(b) 1/2
(c) 1/3
(d) 3/4

Question. A fair coin with 1 marked on one face and 6 on the other and a fair die are both tossed. Then, probability that sum of numbers gives 4.
(a) 1/12
(b) 1/13
(c) 1/15
(d) 1/2

Question. Seven persons are to be seated in a row. The probability that two particular persons sit next to each other, is
(a) 1/3
(b) 1/6
(c) 2/7
(d) 1/2

Question. While shuffling a pack of 52 playing cards, 2 are accidentally dropped. The probability that the missing cards to be of different colours is
(a) 25/52
(b) 26/51
(c) 27/50
(d) 28/49

Question. 4 cards are drawn from a well-shuffled deck of 52 cards. Thus, the probability of obtaining 3 diamonds and one spade is

Question. In a lottery, a person chooses six different natural numbers at random from 1 to 20 and if these six numbers match with the six numbers already fixed by the lottery committee, he wins the prize. Then, the probability of winning the prize in the game is 
(a) 1/38500
(b) 1/38800
(c) 1/38060
(d) 1/ 38760

Question. If A,B and C are three mutually exclusive and exhaustive events of an experiment such that 3P(A) = 2P(B) =P(C), then P(A) is equal to K. Here, K refers to
(a) 1/11
(b) 2/11
(c) 5/11
(d) 6/11

Question. Given, P(A) = 3/5 and P B ( ) = 1/5 . Then, P (A or B), if A and B are mutually exclusive events, is
(a) 2/5
(b) 3/5
(c) 4/5
(d) 1

Question. The probability of getting atmost two tails or atleast two heads in a toss of three coins is
(a) 3/4
(b) 5/8
(c) 7/8
(d) 3/8

Question. Probability that Ram passed in Mathematics is 2/3 and the probability that he passed in English is 4/9. If the probability of passing in both subjects is 1/4, then the probability that Ram will pass in atleast one of these subjects will be
(a) 31/36
(b) 35/36
(c) 1/2
(d) 1/4

Question. Probability that a truck stopped at a roadblock will have faulty brakes and badly worn tires, are 0.23 and 0.24, respectively. Also, the probability is 0.38 that a truck stopped at the roadblock will have faulty brakes or badly worn tires. Then, the probability that a truck stopped at this roadblock will have faulty breaks as well as badly worn tires, is …K… . Here, K refers to
(a) 0.04
(b) 0.07
(c) 0.06
(d) 0.09

Question. A box contains 6 nails and 10 nuts. Half of the nails and half of the nuts are rusted. If one item is chosen at random, then the probability that it is rusted or is a nail, is …K… . Here, K refers to
(a) 3/16
(b) 5/16
(c) 11/16
(d) 14/16

Question. In a simultaneous toss of two coins, the probability of getting exactly 2 tails is m/n . The value of m + n is
(a) 1
(b) 4
(c) 5
(d) 2

Question. An event which has only …… sample point of a sample space, is called simple event.
(a) two
(b) three
(c) one
(d) zero

Question. A single letter is selected at random from the word “PROBABILITY”. The probability that the selected letter is a vowel is
(a) 2/11
(b) 3/11
(c) 4/11
(d) 0

Question. In the following Venn diagram circles A and B represent two events:

The probability of the union of shaded region will be
(a) P(A) + P(B) – 2P(A ∩ B)
(b) P(A) + P(B) – P(A ∩ B)
(c) P(A) + P(B)
(d) 2P(A) +2 P(B) – P(A ∩ B)

Question. If A and B are two events, then the set A∩B denotes the event
(a) A or B
(b) A and B
(c) Only A
(d) Only B

Question. If A and B are mutually exclusive events, then
(a) P(A) ≤ P(B̅)
(b) P(A) ≥ P(B̅)
(c) P(A) < P(B)
(d) None of these

Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
     A B C D
(a) 3 4 2 1
(b) 4 3 1 2
(c) 3 4 1 2
(d) 4 3 2 1

Question. In an experiment, the sum of probabilities of different events is
(a) 1
(b) 0.5
(c) – 2
(d) 0

Question. A die is thrown. Let A be the event that the number obtained is greater than 3. Let B be the event that the number obtained is less than 5. Then P(A∪B) is
(a) 3/5
(b) 0
(c) 1
(d) 2/5

Question. If M and N are any two events, the probability that atleast one of them occurs is …
(a) P(M) + P(N) – 2P(M∩N)
(b) P(M) + P(N) – P(M∩N)
(c) P(M) + P(N) + P(M∩N)
(d) P(M) + P(N) + 2P(M∩N)

Question. If A and B are events such that P(A) = 0.42, P(B) = 0.48 and P(A and B) = 0.16. then,
I. P(not A) = 0.58
II. P(not B) = 0.52
III. P(A or B) = 0.47
(a) Only I and II are correct.
(b) Only II and III are correct.
(c) Only I and III are true.
(d) All three statements are correct.

Question. A die is rolled, let E be the event “die shows 4” and F be the event “die shows even number”. Then
I. E and F are mutually exclusive.
II. E and F are not mutually exclusive.
(a) Only I is true.
(b) Only II is true.
(c) Neither I nor II is true.
(d) Both I and II are true.

Multiple Choice Questions

Question. A bag contains one white and one red ball. A ball is drawn from the bag. If the ball drawn is white it is replaced in the bag and again a ball is drawn, otherwise, a die is tossed. The number of sample point in the sample space of above experiment is
(a) 6
(b) 7
(c) 8
(d) 9

Question. A boy has a ₹ 1 coin, a ₹ 2 coin and a ₹ 5 coin in his pocket. He takes out two coins out of his pocket, one after the other. If Q denotes a ₹ 1 coin, H denotes ₹ 2 coins and R denotes ₹ 5 coins. Then, the sample space for the experiment is
(a) S = (QH, QR,HQ,HR,RH,RQ)
(b) S = (QH, QR, QQ)
(c) S = (QH, QR,HQ,HR)
(d) S = (QH, QR,HQ,HR,RQ)

Question. A coin is tossed three times, consider the following events
A : no head appears.
B : exactly one head appears.
C : atleast two heads appear.
Then,
(a) A, B and C are mutually exclusive events
(b) A, B and C are exhaustive events
(c) Only (a)
(d) Both (a) and (b)

Question. A coin is tossed two times, consider the following events?
E₁ : No head appears.
E₂ : Exactly one head appears.
and E₃ : Atleast one head appears.
They form a set of
(a) mutually exclusive event
(b) exhaustive event
(c) mutually exclusive and exhaustive event
(d) mutually exclusive but not exhaustive event

Question. A set containing the numbers from 1 to 25. Then, the set of event getting a prime number, when each of the given number is equally likely to be selected, is
(a) {2, 3, 7, 11, 13, 17}
(b) {1, 2, 3, 7, 11, 19}
(c) {2, 5, 7, 9, 11, 13, 17, 19, 23}
(d) {2, 3, 5, 7, 11, 13, 17, 19, 23}

Question. If, P(B) = 3/4, P(A ∩ B ∩ C̅) = 1/3 and P(A̅ ∩ B ∩ C̅) = 1/3, then P(B ∩ C) is
(a) 1/12
(b) 1/6
(c) 1/15
(d) 1/9

Question. When the sets A and B are two events associated with a sample space. Then, event ‘A ∪≤B’ denotes
(a) A and B
(b) Only A
(c) A or B
(d) Only B

Question. A bag contains 10 balls, out of which 4 balls are white and the others are non-white. The probability of getting a non-white ball is
(a) 2/5
(b) 3/5
(c) 1/2
(d) 2/3

Question. The probability of raining on day 1 is 0.2 and on day 2 is 0.3. The probability of raining on both the days is
(a) 0.2
(b) 0.1
(c) 0.06
(d) 0.25

Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
     A B C D
(a) 4 3 2 1
(b) 4 2 3 1
(c) 1 3 2 4
(d) 1 2 3 4

Question. A coin is tossed twice. Then, the probability that atleast one tail occurs is
(a) 1/4
(b) 1/2
(c) 1/3
(d) 3/4

Question. An event can be classified into various types on the basis of the
(a) experiment
(b) sample space
(c) elements
(d) None of the above

Question. Events A, B, C are mutually exclusive events such that P(A) = 3x + 1/3, P(B) = 1−x/4 and P(C) = 1−2x/2
The set of possible values of x are in the interval is
(a) [0 , 1]
(b) [1/3, 1/2]
(c) [1/3, 2/3]
(d) [1/3, 13/3]

Question. Let S = {1, 2, 3, 4, 5, 6} and E = {1, 3, 5}, then Ē is
(a) {2, 4}
(b) {3, 6}
(c) {1, 2, 4}
(d) {2, 4, 6}

Question. In rolling a dice, the probability of getting number 8 is 
(a) 0
(b) 1
(c) –1
(d) 1/2

Question. Three identical dice are rolled. The probability that the same number will appear on each of them is:
(a) 1/6
(b) 1/36
(c) 1/18
(d) 3/28

Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
     A B C D
(a) 1 2 3 4
(b) 4 3 2 1
(c) 2 3 4 1
(d) 1 4 2 3

STATEMENT TYPE QUESTIONS 

Question. If E and F are events such that P(E) = 1/4 , P(F) = 1/2 and P(E and F) = 1/8 , then, 
I. P(E or F) = 5/8
II. P(not E and not F) = 3/8
(a) Only I is true.
(b) Only II is true.
(c) Both I and II are true.
(d) Neither I nor II is true.

Question. Consider the experiment of rolling a die. Let A be the event ‘getting a prime number’ and B be the event ‘getting an odd number’. Then, which of the following is true?
I. A or B = A ∪ B= {1, 2, 3}
II. A and B = A ∩ B= {3, 5}
III. A but not B = A – B = {2}
IV. Not A = A’ = {1, 5, 6}
(a) Only I is true
(b) Only II is true
(c) II and III is true
(d) Only IV is true

Question. A card is selected from a pack of 52 cards.
I. The probability that card is an ace of spades, is 2/52 .
II. The probability that the card is black card, is 26/52 .
(a) Only I is false.
(b) Only II is false.
(c) Both I and II are false.
(d) Both I and II are true.

Question. Let S be a sample space containing outcomes ω₁, ω₂, ω₃, …, ω_n i.e., S = {ω₁, ω₂,….,ω_n}. Then, which of the following is true?
I. 0 ≤ P(ω_i) ≤ 1 for each ω_i ∈ S
II. P(ω₁) + P(ω₂) + …. P(ω_n) = 1
III. For any event A, P(A) = ∑P(ω_i) , ω_i ∈ A
(a) Only I
(b) Only II
(c) Only III
(d) All of these

Question. A die is rolled. Let E be the event “die shows 4” and F be the event “die shows even number”. Then, E and F are
(a) mutually exclusive
(b) exhaustive
(c) mutually exclusive and exhaustive
(d) None of the above

Case Based MCQs

There are 4 red, 5 blue and 3 green marbles in a basket.
Based on the above information, answer the following.

Question. If two marbles are picked at randomly, then the probability that both are red marbles is
(a) 3/7
(b) 1/2
(c) 1/11
(d) 1/6

Question. If three marbles are picked at randomly, then the probability that all are green marbles is
(a) 1/220
(b) 1/55
(c) 1/75
(d) 1/80

Question. If two marbles are picked at randomly, then find the probability that both are not blue marbles.
(a) 6/11
(b) 5/12
(c) 7/22
(d) 9/11

Question. If three marbles are picked at randomly, then the probability that atleast one of them is blue, is
(a) 7/12
(b) 37/44
(c) 5/12
(d) 1/44

Question. If three marbles are picked randomly, then the probability that either all are red or all are green.
(a) 7/44
(b) 7/12
(c) 5/12
(d) 1/44

Two students Anil and Vijay appeared in an examination. The probability that Anil will qualify the examination is 0.05 and that Vijay will qualify is 0.10. The probability that both will qualify is 0.02. On the basis of above information, answer the following questions.

Question. Find the probability that Vijay will not qualify the exam.
(a) 0.9
(b) 0.5
(c) 0.8
(d) 0.2

Question. Find the probability that atleast one of them will qualify the exam.
(a) 0.09
(b) 0.13
(c) 0.25
(d) 0.19

Question. Find the probability that atleast one of them will not qualify the exam.
(a) 0.82
(b) 0.74
(c) 0.56
(d) 0.98

Question. Find the probability that both Anil and Vijay will not qualify the exam.
(a) 0.43
(b) 0.67
(c) 0.87
(d) 0.91

Question. Find the probability that only one of them will qualify the exam.
(a) 0.21
(b) 0.11
(c) 0.31
(d) 0.25