Trigonometry MCQ Class 10 Mathematics
Please refer to Chapter 8 Trigonometry MCQ Class 10 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 10 Mathematics. Students should refer to MCQ Questions for Class 10 Mathematics with Answers to score more marks in Grade 10 Mathematics exams. Students should read the chapter Trigonometry and then attempt the following objective questions.
MCQ Questions Class 10 Mathematics Chapter 8 Trigonometry
The Trigonometry MCQ Class 10 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. If 6cot θ + 2cosec θ = cot θ + 5cosec θ, then cos θ is
(a) 4/5
(b) 5/3
(c) 3/5
(d) 5 /4
Answer
C
Question. If tan A =3/2 then the value of cos A is
(a) 3/√13
(b) 2/√13
(c) 2/3
(d) √13/2
Answer
B
Question. The value of 2tan30°/1- tan230° 2 is equal to
(a) cos 60°
(b) sin 60°
(c) tan 60°
(d) sin 30°
Answer
C
Question. If sin θ = 7√85 , what are the values of tan θ, cos θ and cosec θ?
(a) tanθ=6/7 , cosθ=7/√85 and cosecθ=√85/7
(b) tanθ= 7/6, cosθ=7/√85 and cosecθ=√85/7
(c) tanθ=7/6 , cosθ=6/√85 and cosecθ=√85/7
(d) tanθ=7/6 , cosθ=6/√85 and cosecθ=√85/6
Answer
C
Question. Given that sinθ a/b, then cos θ is equal to
(a) b/√b2-a2
(b) b/a
(c) √b2-a2/b
(d) a/√b2-a2
Answer
C
Question.Consider the triangle shown below.
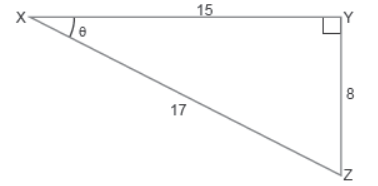
What are the values of tan θ, cosec θ and sec θ?
(a) tanθ=8/15 , cosecθ=17/8 , secθ=17/15
(b) tanθ=8/15 , cosecθ=17/15 , secθ=17/8
(c) tanθ=17/15 , cosecθ=8/15 , secθ=17/8
(d) tanθ=8/15 , cosecθ=17/15 , secθ=8/17
Answer
A
Question. If sin A + sin2 A = 1, then the value of the expression (cos2A + cos4A) is
(a) 1
(b) 1/2
(c) 2
(d) 3
Answer
A
Question. If 4 tan θ = 3, then( 4sinθ – cosθ /4sinθ +cosθ ) is equal to
(a) 2/3
(b) 1/3
(c) 1/2
(d) 3/4
Answer
C
Question. Value of sin 30° tan 45° is
(a) √3/2
(b) 2
(c) 1/2
(d) 0
Answer
C
Question. If cosA =4/5 then the value of tan A is
(a) 3/5
(b) 3/4
(c) 4/3
(d) 5/3
Answer
B
Question. The value of tan260º-sin230º/tan245°+cos230° is
(a) 7/11
(b) 11/13
(c) 13/11
(d) 11/7
Answer
D
Question. If x = r sin θ and y = r cos θ then the value of x2 + y2 is
(a) r
(b) r2
(c) 1/r
(d) 1
Answer
B
Question. If 3 sec θ – 5= 0 then cot i is equal to
(a) 5/3
(b) 4/5
(c) 3/4
(d) 3/5
Answer
C
Question. If α+β = 90° and α = 2β, then cos2α+ sin2β is equal to
(a) 1
(b) 1/2
(c) 0
(d) 2
Answer
B
Question. If sin A=1/2, then the value of cot A is
(a) √3
(b) 1/√3
(c) √3/2
(d) 1
Answer
A
Question. If tan x sin x m and tan x – sin x= n then m2 – n2 is equal to
(a) 4 √mn
(b) √mn
(c) 2 √mn
(d) none of them
Answer
A
Question. 1+tan2A/1+cot2A is equal to
(a) sec2A
(b) –1
(c) cot2 A
(d) tan2 A
Answer
D
Question. sinθ/1-cosθ+cosθ/1-tanθ is equal to
(a) 0
(b) 1
(c) sinθ+cos θ
(d) sinθ – cosθ
Answer
C
Question. Given that sin , then tan b a i = i is equal to
(a) b/√b2-a2
(b) √b2-a2/b
(c) a/√b2-a2
(d) √b2-a2/a
Answer
C
Question. Considering the diagram below.
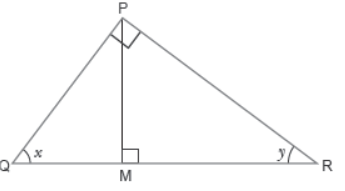
Which of the following statements is true?
(a) Side PR is adjacent to ∠y in triangle PMR and side QR is adjacent to ∠y in triangle PQR
(b) Side MR is adjacent to ∠y in triangle PMR and side PR is adjacent to ∠y in triangle PQR
(c) Side PR is adjacent to ∠y in triangle PMR and side MR is adjacent to ∠y in triangle PQR
(d) Side PR is adjacent to ∠y in triangle PMR and triangle PQR
Answer
B
Question. The two legs AB and BC of right triangle ABC are in a ratio 1 : 3. What will be the value of sin C?
(a) √10
(b) 1/√10
(c) 3/√10
(d) 1/2
Answer
B
Question. The value of (sin 30° + cos 30°) – (sin 60° + cos 60°) is
(a) – 1
(b) 0
(c) 1
(d) 2
Answer
B
Question. The value o tan30 °/ cot60° is
(a) 1/√2
(b) 1/√3
(c) √3
(d) 1
Answer
D
Question. The value of 4-sin245° /cot k tan60º is 3.5.
What is the value of k?
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer
C
Question. Which of these is equivalent to 2tanx(sec2x-1)/cos3x ?
(a) 2 tan3 x cosec x
(b) 2 cot3 x cosec3 x
(c) 2 tan3 x sec3 x
(d) 2 cot3 x sec3 x
Answer
C
Question. If sin θ + cos θ = √2 cos θ, (θ ≠ 90) then the value of tan θ is
(a) √2 – 1
(b) √2 +1
(c) √2
(d) – √2
Answer
A
Question. Which of the following option makes the statement below true?
1/secx+secx/cos2 x-1-tan2 x
(a) −cosec x tan x
(b) −sec x tan x
(c) −cosec x cot x
(d) −sec x cot x
Answer
C
Question. If sec i+tan i = x, the value of sec i is
(a) 1/2(x-1/x)
(b) x2-1/x2+1
(c) 1/2(x+1/x)
(d) none of them
Answer
C
Question. If sinθ= 1/3, the value of (2cot2 θ + 2) is
(a) 16
(b) 20
(c) 12
(d) 18
Answer
D
Question. (cosec θ – sin θ) (sec θ – cos θ) (tan θ + cot θ) is equal to
(a) 0
(b) 1
(c) –1
(d) none of these
Answer
B
Question. (sec A + tan A) (1 – sin A) is equal to
(a) sec A
(b) sin A
(c) cosec A
(d) cos A
Answer
D
Question. The value of √1+cosθ/1-cosθ
(a) cotθ– cosecθ
(b) cosecθ+cotθ
(c) cosec2θ+ cot2θ
(d) (cotθ+ cosecθ )2
Answer
B
Question. Given that sinα= 1/2 and cos β=1/2, then the value of (a + b) is
(a) 0°
(b) 30°
(c) 60°
(d) 90°
Answer
D
Question. The value of (1 + cot θ – cosec θ)(1 + tan θ + sec θ) is
(a) 1
(b) 2
(c) –1
(d) None of these
Answer
B
Question. If sin 77° = x, than the value of tan 77° is
(a) 1/1+x2
(b) x/√1+x2
(c) x/√1-x2
(d) None of these
Answer
C
Question. sec4 A – sec2 A is equal to
(a) tan2A – tan4A
(b) tan4A – tan2A
(c) tan4A + tan2A
(d) None of these
Answer
C
Question. If a cos θ + b sin θ = m and a sin θ – b cos θ = n, then a2 + b2 is equal to
(a) m2 – n2
(b) m2n2
(c) n2 – m2
(d) m2 + n2
Answer
D
Question. If x = a cos θ and y = b sin θ, then the value of b2x2 + a2y2 is
(a) a2 + b2
(b) a2/b2
(c) a2b2
(d) None of these
Answer
C
Question. If √3 tan θ = 3 sin θ, (θ ≠ 0) then the value of sin2 θ – cos2 θ is
(a) 1/3
(b) 3
(c) 2/3
(d) 3/2
Answer
A
Question. If cos A + cos2A = 1, then sin2A + sin4A is equal to
(a) –1
(b) 0
(c) 1
(d) None of these
Answer
C
Question. The value of (sin 45° + cos 45°) is
(a) 1/√2
(b) √2
(c) √3/2
(d) 1
Answer
B
Question. What is the value of 3-sin260º/tan30ºtan60º ?
(a) 21/4
(b) 31/4
(c) 2 3/4
(d) 3 3/4
Answer
A
Question. If 4 tan x = 3, than cos x +sin x/cos x-sin x is equal to
(a) 7
(b) 1/7
(c) – 7
(d) –1/7
Answer
A
Question. cos4 A – sin4 A is equal to
(a) 2cos2A + 1
(b) 2cos2A – 1
(c) 2sin2A – 1
(d) 2sin2 A + 1
Answer
B
Question. sinθ/1+cosθ is equal to
(a) 1+cosθ/sinθ
(b) 1+cosθ/cosθ
(c) 1-cosθ/sinθ
(d) 1-sinθ/cosθ
Answer
C
Question. The value of the expression sin 60°/cos30º is
(a) √3/2
(b) 1/2
(c) 1
(d) 2
Answer
C
Question. If 2x = sec θ and tan 2/x = tanθ , then the value of (x2-1/x2) is
(a) 4
(b) 1/4
(c) 2
(d) 1/2
Answer
B
Question. Value of cos 0° ⋅ cos 30° ⋅ cos 45° ⋅ cos 60° ⋅ cos 90° is
(a) 0
(b) 1
(c) 2
(d) 9
Answer
A
Question. ABC is a triangle right angled at C and AC = √3 BC. Then ∠ABC =
(a) 30°
(b) 60°
(c) 90°
(d) 0°
Answer
B
Question. The value of sin 60° ⋅ cos 30° + sin 30° ⋅ cos 60° is
(a) 0
(b) 1
(c) 2
(d) 8
Answer
B
Question. If sin (A + B) = √3/2 and sin 2B = 1/ 2 , then
(a) tan B = 1
(b) B = 30°
(c) B = 45°
(d) cosA 1/ 2
Answer
C
Question. If x = a (cosec θ + cot θ) and y = b(1 cos )/ sinθ − , then xy =
(a) a2 + b2/ a2– b2
(b) a2 – b2
(c) ab
(d) a b
Answer
C
Question. If x = p sec q and y = q tan θ , then
(a) x2 – y2 = p2q2
(b) x2q2 – y2p2 = pq
(c) x2q2 – y2p2 = 1/p2q2
(d) x2q2 – y2p2 = p2q2
Answer
D
Question. If p sin θ + q cos θ = a and p cos θ – q sin θ = b, then p+a/q+b + q-b/p-a =
(a) 1
(b) a2 + b2
(c) 0
(d) 2
Answer
C
Question. If cosec A + cot A = 11/ 2 , then tan A
(a) 21/ 22
(b) 15/ 16
(c) 44 /117
(d) 11 /117
Answer
C
Question. 2tan30°/1+ tan 30 ° + ° is equal to
(a) sin 30°
(b) cos 60°
(c) 1/ 2
(d) √3/2
Answer
D
Question. If x = r sinA cos C, y = r sin A sin C, z = r cos A, then
(a) r2 = x2 + y2 + z2
(b) r2 = 2xy
(c) r2 = x + y + z
(d) r2 = y2 + z2 + 2xy
Answer
A
Question. If tan2θ = 1– a2, then the value of sec θ + tan3θ cosec θ is
(a) (2 – a2)
(b) (2 – a2)1/2
(c) (2 – a2)2/3
(d) (2 – a2)3/2
Answer
D
Question. If x = a cos2θ + b sin2θ, then (x – a) (b – x) is equal to
(a) (a – b) sinθ cosθ
(b) (a – b)2 sin2θ cos2θ
(c) (a – b)2 sinθ cosθ
(d) (a – b) sin2θ cos2θ
Answer
B
Question. If cos A = 3/ 5 , find the value of 9 cot2A – 1.
(a) 1
(b) 16/ 65
(c) 65 /16
(d) 0
Answer
C
Question. 2tan30°/ 1+ tan230 ° =
(a) sin 60°
(b) cos 60°
(c) tan 60°
(d) sin 30°
Answer
A
Question. 9 sec2 A – 9 tan2 A =
(a) 1
(b) 9
(c) 8
(d) 0
Answer
B
Question. cos 1° . cos 2°. cos 3° ……… cos 179° is equal to
(a) –1
(b) 0
(c) 1
(d) 1/√2
Answer
B
Question. If (sec2θ) (1 + sinθ) (1 – sinθ) = k, then find the value of k.
(a) sinθ
(b) secθ
(c) 1
(d) cotθ
Answer
C
Question. sin2q + cosec2q is always
(a) greater than 1
(b) less than 1
(c) greater than or equal to 2
(d) equal to 2
Answer
C
Question. sin 2A = 2 sin A is true when A =
(a) 0°
(b) 30°
(c) 45°
(d) 60°
Answer
A
Question. If b tan θ = a, the value of asinθ-bcosθ/asinθ + bcosθ is
(a) a – b/a2 + b2
(b) a + b/ a2 + b2
(c) a2 + b2/ a2– b2
(d) a2– b2/ a2 + b2
Answer
D
Question. (cos4A – sin4A) is equal to
(a) 1 – 2 cos2A
(b) 2 sin2 A – 1
(c) sin2A – cos2A
(d) 2 cos2A – 1
Answer
D
Question. If cosθ/1-sinθ + cosθ/1+sinθ= 4, then
(a) cosθ =√3 /2
(b) sinθ = 1/ 2
(c) θ = 60°
(d) tanθ = 1/√3
Answer
C
Question. 2 tan30°/ 1- tan2 30° =
(a) cos 60°
(b) sin 60°
(c) tan 60°
(d) sin 30°
Answer
C

We hope you liked the above Trigonometry MCQ Class 10 Mathematics. In case you have any questions please put them in the comments box below and our teachers will provide you a response.


