Please see below Class 12 Mathematics Sample Paper Set F with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.

CBSE Sample Paper for Class 12 Mathematics Set F

Part–A
Section – I

All questions are compulsory. In case of internal choices attempt any one.

Q1. Check whether the function f : N → N, given by f(x) = 2x, is one-one or not. 
Answer : f (x) is one-one.

OR

Write the name of a relation which is reflexive, symmetric and transitive.
Answer : Equivalence relation

Q2. State the reason of the relation R in the set {1, 2, 3} given by: R = {(1, 2), (2, 1)} not to be transitive. 
Answer : Relation R is not transitive because (1, 2), (2, 1) ∈ R but (1, 1) ∉ R.

Q3. How many relations are possible in set A = {2, 4, 7, 9}? 
Answer : 2¹⁶

OR

Let R be the equivalence relation in the set A = {0, 1, 2, 3, 4, 5} given by R = {(a, b) : 2
divides (a – b)}. Write the equivalence class [0].
Answer : {0, 2, 4}

Q4.  

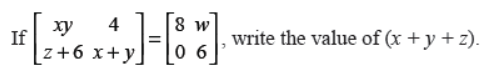
Answer : 0

Q5.  

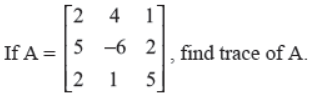
Answer :  1

OR

If A =  

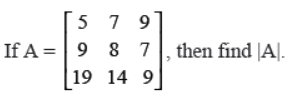
Answer : 0

Q6. Find the adjoint of matrix
Answer : 

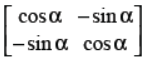
Q7. Evaluate 

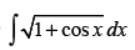
Answer :

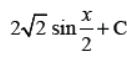
OR

Evaluate:
Answer : 1

Q8. Find the area bounded by the line y = x, the x-axis and the ordinate x = 2.
Answer : 2 sq. units

Q9. Form the differential equation representing the family of curves x² + y² = a² by eliminating arbitrary constant ‘a’.
Answer : x + yy′ = 0

OR

Solve: DY/DX + 2x = e3x 
Answer : y =1/3 e3x–x2+C

Q10. Write the position vector of the point A (2,1, –3). 
Answer : 2𝑖̂ + 𝑗̂− 3𝑘̂

Q11. Write the position vector of the mid-point of AB if A( 3, 4, – 2) and B(1, 2, 4). Use vector method. 
Answer : 2𝑖̂ + 𝑗̂+ 3𝑘̂

Q12. Find the unit vector in the direction of the vector a̅ = 3iˆ − 6𝑗̂ + 2𝑘̂. 
Answer :  

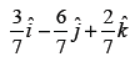
Q13. Find the vector equation of the straight line passing through the points (2, 1, – 3) and (5, –4, 1). 
Answer :  

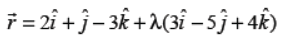
Q14. Write the intercept cut off by the plane 2x + y – z = 5 on x-axis. 
Answer : 5/2

Q15. Compute P(A|B) if P(B) = 0.5 and P(A ∩ B) = 0.32. 
Answer : 0.64

Q16. A and B throw a coin alternately till one of them gets a ‘head’ and wins the game. Find the probability of winning of A.
Answer : 2/3

Section-II

Both the Case study-based questions are compulsory. Attempt any 4 sub-parts from each question (17–18). Each sub-part carries 1 mark.

Q17. A ladder 5m long is leaning against a wall. The bottom of the ladder is pulled along the ground away from the walk at the rate of 2 cm/sec.

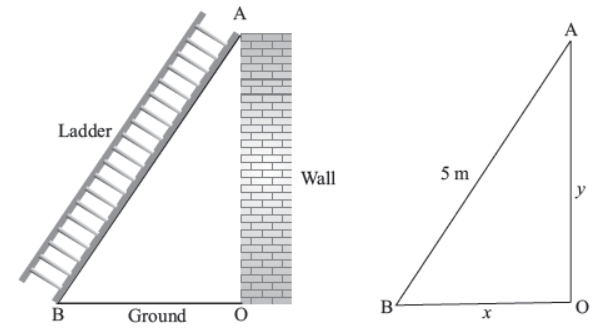
Based on the above information, answer the following.

(i) Relation between x and y is 1
(a) x² + y² = 52
(b) x² = 52 + y²
(c) y² = x2
(d) 2x² + y² = 52
Answer : A

(ii) The decreasing rate of wall’s height in terms of x and y is  

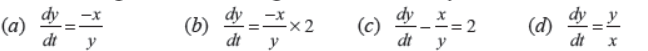
Answer : B

(iii) For x = 4, the value of y will be 
(a) 2
(b) 1
(c) 3
(d) 0
Answer : C

(iv) Value of dy/dx by putting the correct value of y for x = 4 is
(a) −8/5 m/sec
(b) −8/7 m/sec
(c)−8/9 m/sec
(d) −8/3 m/sec
Answer : D

(v) How fast is the height on the wall decreasing when the foot of the ladder is 4 m away from the wall? 
(a) 8/3 m/sec
(b) 8/7 m/sec
(c) 8/5 m/sec
(d) 8/9 m/sec
Answer : A

Q18. A company has two plants to manufacture motorbikes. 70% motorbikes are manufactured at the first plant, while 30% are manufactured at the second plant. At the first plant, 80% motorbikes are rated of the standard quality while at the second plant, 90% are rated of standard quality. 

Based on the above information answer the following:
(i) What is the probability that the motorbikes are manufactured at the first plant i.e.,P(plant I)? 
(a) 7/10
(b) 5/9
(c) 4/9
(d) 3/10
Answer : A

(ii) What is the probability that the motorbikes are manufactured at the second plant i.e., P(plant II)? 
(a) 1/5
(b) 3/10
(c) 3/5
(d) 7/10
Answer : B

(iii) Find P (E|plant I), where E denotes the event that motorbike is of standard quality. 
(a) 1/5
(b) 4/5
(c) 1/3
(d) 2/3
Answer : B

(iv) Find P (E|plant II), where E denotes the event that motorbike is of standard quality. 
(a) 1/10
(b) 3/5
(c) 9/10
(d) 7/10
Answer : C

(v) A motorbike, randomly picked up is found to be of standard quality. Find the probability that it has come out from the second plant. 
(a) 72/83
(b) 72/85
(c) 27/38
(d) 27/83
Answer : D

Part–B
Section–III

All questions are compulsory. In case of internal choices attempt any one.

Q19. Find the value of

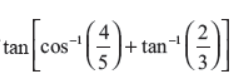
Answer : 17/6

Q20. Prove that 

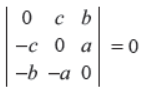
Answer : …….

OR

Find the value of the determinant  

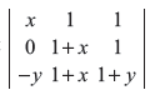
Answer : xy(x + 2)

Q21. Examine the continuity of the function  

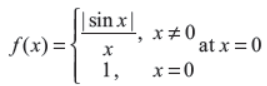
Answer : f (x) is discontinuous at x = 0.

Q22. Determine the equation of the normal line to the curve y = 3√5 − x at the point (– 3, 2). 2
Answer : 12x – y + 38 = 0

Q23. Evaluate  

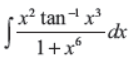
Answer : 1/6(tan^–1 x³)² + C

Q24. Find the area of the region bounded by the parabola y = x2 and the lines y = |x|
Answer : 1/3 sq. units

Q25. Solve dy/dx + y tanx = sec x
Answer : y sec x = tan x + C

Q26. Given that a̅.b̅ = 0 and a̅ × b̅ = 0 . What can you conclude about the vectors a̅ and b̅. 
Answer : Either a̅ = 0 or b̅ = 0

Q27. Find the equation of the plane through the point (1, 4, – 2) which is parallel to the plane – 2x + y – 3z = 0. 
Answer : –2x + y – 3z = 8

Q28. Let A and B be two independent events such that P(A) = 0.4, P(B) = p and P(A ∪ B) = 0.7. Find the value of p for which A and B are independent.
Answer : P = 1/2

OR

A die is tossed thrice. Find the probability of getting an odd number at least once.
Answer : 7/8

Section-IV

All questions are compulsory. In case of internal choices attempt any one.

Q29. Show that the relation R defined in the set A of all triangles as R = {(T₁, T₂) : T₁ is similar to T₂} is an equivalence relation. Consider three right angle, triangles, T₁ with sides 3, 4, 5, T2 with sides 5, 12, 13 and T₃ with sides 6, 8, 10. Which triangles among T₁, T₂ and T₃ are related?
Answer : Triangle T₁ is related to triangle T₃.

Q30. If sin(xy) = x cos y, find
Answer : cos y – y cos xy/ xcos xy + xsiny

Q31. If

Answer : ……

OR

If y = cot x + cosec x, then show that sinx d²y/dx² = y².
Answer : …..

Q32. Find the maximum and minimum value of f (x) = x3 – 12×2 + 36x + 17 in 1 ≤ x ≤ 10.
Answer : Absolute maximum value is 177 at x = 10 and absolute minimum value is 17 at x = 6.

Q33. Evaluate each of the following integrals 

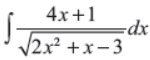
Answer : 2√2x²+x−3+C

Q34. Find the area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the line x = 0 and x = 2.
Answer : π sq. units

OR

Find the area lying between the curves y2 = 4x and y = 2x.
Answer : 1/3 sq. units

Q35. Solve the following differential equation  (1 + x²)dy + x √1− y² dx = 0.
Answer : sin^–1 y + 1/2 log |1 + x² | = C

Section-V
All questions are compulsory. In case of internal choices attempt any one.

Q36. If A   

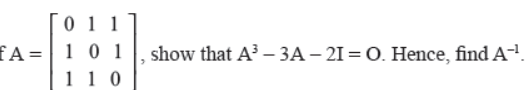
Answer : 

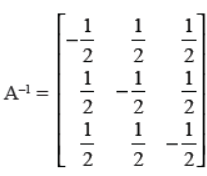
OR

For the matrix

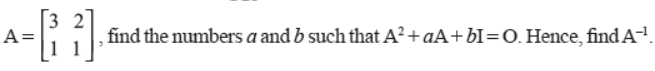
Answer : 

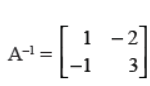
Q37. Find the vector equation of the line which passes through the point (1, 2, 3) and parallel to the vector 𝑖̂ − 2 𝑗̂ + 3𝑘̂. Deduce the corresponding equation in Cartesian form.
Answer : Vector equation is r̅ = 𝑖̂ + 2 𝑗̂ + 3𝑘̂ + λ(𝑖̂ − 2 𝑗̂ + 3𝑘̂) 

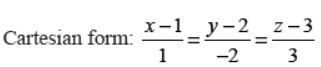
OR

Find the equation of the plane containing the line x−3/2 = y+2/9 = 4−z/1 and the point (– 6, 3, 2).
Answer : x – y – 7z + 23 = 0

Q38. Solve the following linear programming problem (L.P.P.) graphically. 
Maximize profit P = x + 2y subject to constraints;
x + y < 24
x + 2y < 32
x > 0
y > 0
Answer : Maximum value of P is 32 at (16, 8) and (0, 16).

OR

Shade the feasible region determined by the minimise function Z = x + 2y, subject to constraints
2x + y > 3
x + 2y > 6
x, y > 0
on given graph. Also verify that the minimum of Z occurs at more than two points. 

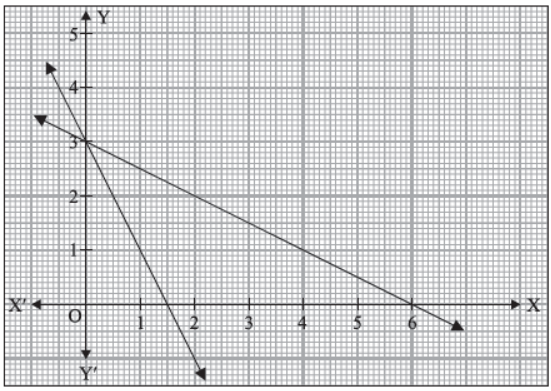
Answer : ……….