Please see below Class 12 Mathematics Sample Paper Set G with solutions. We have provided Class 12 Mathematics Sample Papers with solutions designed by Mathematics teachers for Class 12 based on the latest examination pattern issued by CBSE. We have provided the following sample paper for Class 12 Mathematics with answers. You will be able to understand the type of questions which can come in the upcoming exams.

CBSE Sample Paper for Class 12 Mathematics Set G

Part–A
Section – I

All questions are compulsory. In case of internal choices attempt any one.

Q1. Check whether the function f (x) = x² ∀ x ∈ Z is many-one or not.
Answer : Yes, f (x) is many one function.

OR

If R = {(x, y) : x + 2y = 8} is a relation on N, write the domain of R.
Answer : {2, 4, 6}

Q2. A relation R in set A is such that (a, a) ∈ R ∀ a ∈ A. Write the name of the relation.
Answer : Reflexive Relation

Q3. Write the principal value of tan–1 (1/√3).
Answer : π/6

OR

Write the principal value branch of cos^–1x.
Answer : [0, π]

Q4. In the matrix A

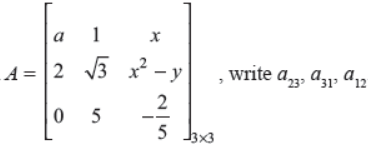
Answer : a₂₃ = x² – y, a₃₁ = 0, a₁₂ = 1

Q5. If A  

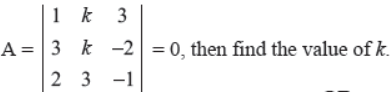
Answer : k = 33/8

OR

Find the value of

Answer : 0

Q6. Find the area of the triangle with vertices (0, 0), (6, 0) and (4, 3).
Answer : 9 sq. units

Q7. Evaluate: ∫ex (sin x + cos x) dx
Answer : e^x sin x + C

OR

Evaluate:

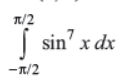
Answer : 0

Q8. Write the area bounded by the curve x = f (y), where x lies the right of y-axis, the y-axis, and the abscissae y = c and y = d. 
Answer : 

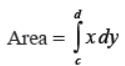
Q9. Determine the order of the differential equation: y ≤ + 4y = 0.
Answer : 2

OR

Find the I.F of differential equation y′ + 2y = e3x.
Answer : e^2x

Q10.   

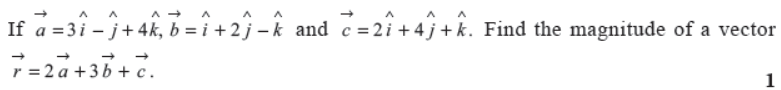
Answer : √221

Q11. 

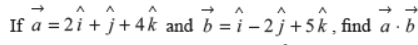
Answer : 20

Q12. For given vectors a̅ = 2î − ĵ − 2k̂ and b = −î + ĵ − k̂, find the unit vector in the direction of a̅ + b̅.
Answer : 1/√2î + 1/√2k̂

Q13. Find the vector equation of the line joining the points whose position vectors are 2î − ĵ + k̂ and î + 2 ĵ − 3k̂.
Answer : r̅ = 2î − ĵ + k̂+λ(î + 3 ĵ − 4k̂)

Q14. Find the value of k for which the planes 3x – 6y – 2z = 7 and 2x + y – kz = 5 are perpendicular to each other.
Answer : 0

Q15. Given P(A) = 3/5 and P (B) = 1/5 . Find P(A ∩ B) if A and B are independent events. 
Answer : 3/25

Q16. An urn contains 7 red and 4 blue balls. Two balls are drawn at random with replacement.
Find the probability of getting 2 red balls.
Answer : 49/121

Section-II
Both the Case study-based questions are compulsory. Attempt any 4 sub-parts from each question (17–18). Each sub-part carries 1 mark.

Q17. A window has the shape of a rectangle surmounted by an equilateral triangle. Perimeter of the window is 12 m. 

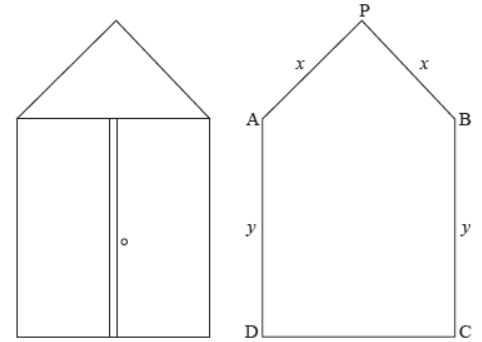
Based on the above information answer the following:
(i) If x and y represents the length and breadth of the rectangular region, then the relation between the variables is 1
(a) 3x + 2y = 12
(b) 3x + y = 12
(c) x + y = 6
(d) x + 2y = 6
Answer : A

(ii) The area of the window in terms of x is  

Answer : B

(iii) Maximum value of area is  

Answer : C

(iv) Area is maximum, when x = 

Answer : D

(v) For value of x obtained from (iv), y will be  

Answer : B

Q18. In a hockey match, both teams A and B scored same number of goals up to the end of the game.
So as to decide the winner, the referee asked both the captains to throw a die alternatively and decided that the team, whose captain get a six first, will be declared the winner. 

Based on the above information answer the following:
(i) What is the probability of throwing six when a die is thrown? 
(a) 1/6
(b) 5/6
(c) 2/6
(d) 3/6
Answer : A

(ii) What is the probability of not throwing six? 
(a) 1/6
(b) 5/6
(c) 2/6
(d) 3/6
Answer : B

(iii) Probability that the captain of team A can win in 1st, 3rd, 5th……..throws is 
(a) 5/11
(b) 6/11
(c) 3/11
(d) 2/11
Answer : B

(iv) Probability that the captain of team B can win is 
(a) 1/11
(b) 2/11
(c) 5/11
(d) 3/11
Answer : C

(v) The decision of referee was not fair because 
(a) P(A win) = P (B win)
(b) P(A win) < P (B win)
(c) P(A win) > P (B win)
(d) P(A win) = 0
Answer : C

Part–B
Section–III

All questions are compulsory. In case of internal choices attempt any one.

Q19. Find the value of the following expression: cos–1 (cos 13π/6)
Answer : π/6

Q20. Compute the adjoint of the matrix

Answer : Adj 

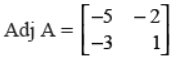
OR

Using matrix method, solve the following: 2x – y = 7, x + 3y = 21.
Answer : x = 6, y = 5

Q21. Show that the function  

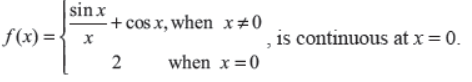
Answer : 

Q22. Find the equation of tangent at (– 4, – 4) on the curve x² = – 4y.
Answer : 2x – y + 4 = 0

Q23. Evaluate:  

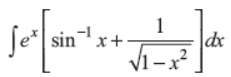
Answer : e^x sin^–1 x + C

Q24. Find the area under the graph of y = x over the interval [2, 4]. 
Answer : 3 sq. units

Q25. Verify that y = 2(x² – 1) + Ce–x² is a solution of the differential equation dy/dx + 2xy = 4x³. 
Answer : 

Q26. Show that the vectors 2î − 3 ĵ + 4k̂ and −4î + 6 ĵ − 8k̂ are parallel. 
Answer : 

Q27. Find the equation of the plane through the point 2î + ĵ − 3k̂ that is parallel to the plane r̅. (î − 2ĵ) = 7 .
Answer : r̅. (î − 2ĵ) = 0

Q28. A card is drawn from a well shuffled deck of 52 cards. Then events A and B are: A : getting a card of spade, B : getting an ace. Determine whether the events A and B are independent or not. 
Answer : A and B are independent events.

OR

The odds are 9 to 5 against a person who is 50 years living till he is 70 and 8 to 6 against a person who is 60 living till he is 80. Find the probability that at least one of them will be
alive 20 years.
Answer : 31/49

Section-IV
All questions are compulsory. In case of internal choices attempt any one.

Q29. Let A = {a, b, c, d} and R = A × A. Show that R is an equivalence relation on set A. 
Answer : 

Q30. Find dy/dx , where x and y are given by x = 3 cos t – 2 cos3 t and y = 3 sin t – 2 sin3 t. 
Answer : cot t

Q31. Prove that the function f(x) = 1 + |sin x| is not differentiable at x = 0. 
Answer : …….?

OR

If x = cos θ + θ sin θ, y = sin θ – θ cos θ, then find d²y/dx².
Answer : Sec3θ/θ

Q32. Find local maximum and local minimum, if any, of following function: f (x) = 2/x − 2/x² , x > 0
Answer : x = 2 is a point of local maxima and local maximum value is 1/2

Q33. Evaluate: ∫ dx/(2 − x) (x² + 3).
Answer :

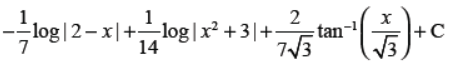
Q34. Find the area bounded by the curve y = sin x between x = 0 and x = 2π. 
Answer : 4 sq. units

OR

Sketch y = x and y2 = 16x and find the area enclosed between them.
Answer : 128/3sq units

Q35. Find the general solution of differential equation: 
sec² x tan y dx + sec2 y tan x dy = 0.
Answer : | tan x tan y | = C, where x, y ∈ R –(odd multiple of π/2)

Section-V
All questions are compulsory. In case of internal choices attempt any one.

Q36. If  

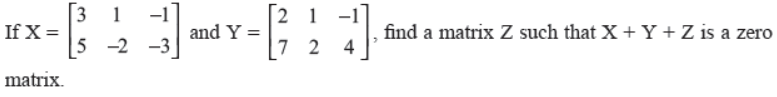
Answer : 

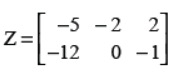
OR

Find non-zero values of x satisfying the matrix equation 

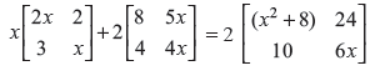
Answer : x = 0, 4

Q37. Find the vector equation of the straight line passing through (1, 2, 3) and perpendicular to the plane r̅ (î + 2ĵ− 5k̂) + 9 = 0 .
Answer : r̅(î + 2ĵ + 3k̂) + λr̅(î + 2ĵ – 5k̂)

OR

Find the Cartesian equation of the line passing through (1, 2, 3) and parallel to the planes
r̅(î − ĵ + 2k̂) = 5 and r̅(3î + ĵ + k̂) = 6 .
Answer : x–1/–3 = y–2/5 = z–3/4

Q38. Solve the following linear programming problem (L.P.P.) graphically. 5
Minimize Z = 150 x + 200 y subject to constraints:
3x + 5y ≥ 30
x + y ≥ 8
x ≥ 0, y ≥ 0
Answer : Minimum value of Z is 1350 occurs at the point (5, 3).

OR

Find the linear constraints for which the shaded area in the figure below is the solution set. 

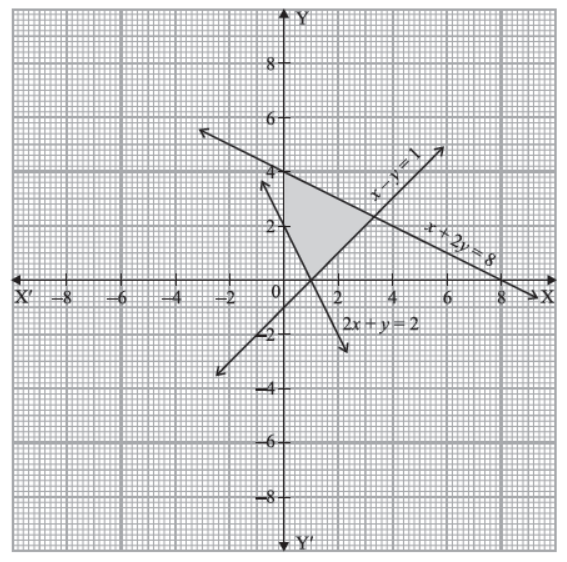
Answer : 
x + 2y ≤ 8;
2x + y ≥ 2
x – y ≤ 1
x, y ≥ 0