Complex Numbers and Quadratic Equations MCQ Class 11 Mathematics
Please refer to Chapter 5 Complex Numbers and Quadratic Equations MCQ Class 11 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 11 Mathematics. Students should refer to MCQ Questions for Class 11 Mathematics with Answers to score more marks in Grade 11 Mathematics exams. Students should read the chapter Complex Numbers and Quadratic Equations and then attempt the following objective questions.
MCQ Questions Class 11 Mathematics Chapter 5 Complex Numbers and Quadratic Equations
The Complex Numbers and Quadratic Equations MCQ Class 11 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question: a +ib > c + id can be explained only when
(a) b = 0, c = 0
(b) b = 0, d = 0
(c) a = 0, c = 0
(d) a = 0, d = 0
Answer
B
Question: If x iy= 3/2+cosθ+isinθ, then x2+ y2 is equal to
(a) 3x – 4
(b) 4x – 3
(c) 4x + 3
(d) None of these
Answer
B
Question: The imaginary part of
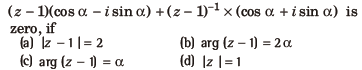
Answer
C
Question: If a = cosθ +isin θ, then 1+a/1-a is equal to
(a) cot θ/2
(b) cot θ
(c) i cot θ/2
(d) i tan θ/2
Answer
C
Question:
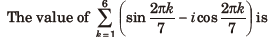
(a) -1
(b) 0
(c) – i
(d) i
Answer
D
Question: If a = cos α + isin α, b = cos β + isin β ,c = cosy+ isin y and b/c +c/a +a/b =1,then cos (β – y ) + cos (y – α) + cos (α – b) is equal to
(a) 3/2
(b) – 3/2
(c) 0
(d) 1
Answer
D
Question:
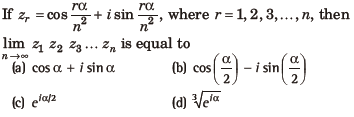
Answer
C
Question: The values of (16)1/4 are
(a) ±2, ± 2 i
(b) ±4 , ± 4 i
(c) ±1, ± i
(d) None of these
Answer
A
Question: If cos α + cos β + cos y = sin α + sin β + sin y = 0, then cos 3α + cos 3 β + cos 3 y is equal to
(a) 0
(b) cos (α+ β + y)
(c) 3 cos (α + β + y)
(d) 3 sin(α+ β + y)
Answer
C
Question: The value of a+bω+cω2/b+cω+aω2+a+bω+cω2/c+aω+ω2 is
(a) 1
(b) -1
(c) 2
(d) -2
Answer
B
Question: If x = a + b,y = aα + bβ and z = αβ+bα, where α and β are com plex cube roots of unity, then xyz is equal to
(a) a2 + b2
(b) a3 + b3
(c) a3 b3
(d) a3 – b3
Answer
B
Question: Let ωn=cos(2π/n)+jsin(2π/n),j2=-1,then(x+Yω3+zω23(x+yω23+zω3)is equal to
(a) 0
(b) x2+ y2 +z2
(c) x2+ y2+ z2– yz -zx -xy
(d) x2+y2+z2+yz+zx+xy
Answer
C
Question: If ω(≠1) is a cube root of unity and (1+ω)7 = A + Bω, then A and B are re spec tively
(a) 0 , 1
(b) 1, 1
(c) 1, 0
(d) -1, 1
Answer
B
Question: If α β and y are the cube roots of a pos i tive number p, then for any real x, y and z, the express ion.
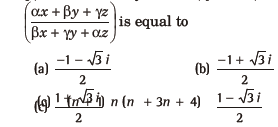
Answer
A
Question: If 1,ω and ω2 are the cube roots of unity, then
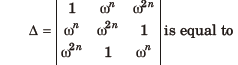
(a) 0
(b) 1
(c) ω
(d) ω2
Answer
A
Question:
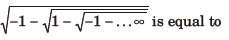
(a) 1
(b) –1
(c) ω2
(d) – ω
Answer
C
Question:

Answer
B
Question:

(a) ω, ω2
(b) ω, ω3
(c) ω2 ω3 ,
(d) None of these
Answer
A
Question: The value of (1+ ω2 +2ω)3n -(1+ω +2ω2)3n is equal to
(a) 0
(b) 1
(c) ω
(d) ω2
Answer
A
Question:
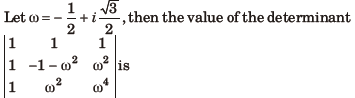
(a) 3ω
(b) 3ω(ω -1)
(c) 3 ω2
(d) 3ω(1 -ω)
Answer
B
Question:
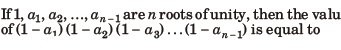
(a) √3
(b) 1/2
(c) n
(d) 0
Answer
C
Question: If ω is a com plex cube root of unity, then for positive in tegral value of n, the product of ω. ω2.ω3... ωn will be
(a)1-i √3/2
(b) -1-i √3/2
(c) 1
(d) Both(b) and (c)
Answer
D
Question: Locus of z, if arg(z-1/z+1)=π/2, is
(a) a circle
(b) a semi-circle
(c) a straight line
(d) None of these
Answer
B
Question:
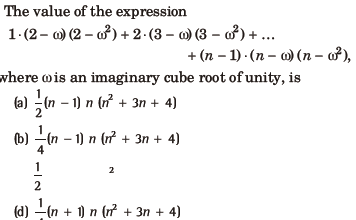
Answer
B
Question: The locus of the points z which sat isfy the condi tion arg(z-1/z+1)=π/3,is
(a) a straight line
(b) a circle
(c) a parabola
(d) None of these
Answer
B
Question: If z1, z2, z3. and z4 are the af fixes of four points in the argand plane and z is the af fix of a point, such that
|z – z1|=|z – z2 |=|z – z3 |=|z – z4 |,then z1, z2, z3 and z4 are
(a) concyclic
(b) vertices of a parallelogram
(c) vertices of a rhombus
(d) in a straight line
Answer
A
Question: If the area of the triangle on the complex plane formed by the points z, z + iz and iz is 200, then the value of |3 z| must be equal to
(a) 20
(b) 40
(c) 60
(d) 80
Answer
C
Question: Let z be a complex number and a be a real parameter such that z2+ax+a2 = 0, then
(a) locus of z is a pair of straight lines
(b) locus of z is a circle
(c) arg (z) = ± 5π/3
(d) |z | = – 2|a |
Answer
A
Question: Re( z2) = 1 is rep resented by
(a) the circle x2+ y2 = 1
(b) the hyperbola x2- y2 = 1
(c) parabola or a circle
(d) All of these
Answer
B
Question: If Im(z-1/2z+1)=-4, then locus of z is
(a) an ellipse
(b) a parabola
(c) a straight line
(d) a circle
Answer
D
Question: If n is a positive integer, then(1+i/1+i)4n+1is equal to
(a) 1
(b) -1
(c) i
(d) -i
Answer
C
Question: The conjugate of complex number 2-3i/4-i is

Answer
B
Question: Let z1and z2 be two complex numbers such that z1+ z2 and z1 z2 both are real, then

Answer
B
Question:

Answer
B
Question: If z-i/z+i/z+1 (z≠-1) is purely imaginary number, then z–z is equal to
(a) 0
(b) 1
(c) 2
(d) None of these
Answer
B
Question: If
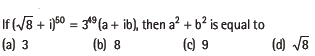
(a) 3
(b) 8
(c) 9
(d) 8
Answer
C
Question:

Answer
C
Question: For any complex number z, the minimum value of |z| + |z – 2i| is equal to
(a) 0
(b) 1
(c) 2
(d) None of these
Answer
C
Question: If arg z < 0, then arg (- z) – arg (z) is equal to
(a) π
(b) – π
(c) – π/2
(d )π/2
Answer
A
Question: The value of the expression

Answer
B
Question: The square root of (- 15 – 8i) is
(a) ± (1- 4i)
(b) ± (1+ 4i)
(c) ± (- 2 + 4i)
(d) None of these
Answer
A
Question:
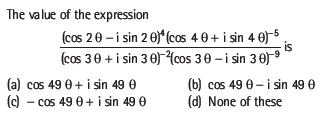
Answer
B
Question: The common roots of the equations
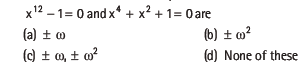
Answer
C
Question: One root of the equation z2– az+ a- 1 = 0, is (1+ i), where a is a complex number, then other root is
(a) 1
(b) 1+ i
(c) 1- i
(d) None of these
Answer
A
Question:

(a) 0
(b) 32
(c) 10
(d) 2
Answer
A
Question: If iz4 + 1= 0, then z can take the value

Answer
B
Question:

Answer
A
Question: If |z1 |=|z2|z3|= 1and z1 + z2 + z3 = 0, then the area of triangle whose vertices are z1, z2 and z3, is
(a)3 √3/4
(b)3/4
(c) 1
(d)2
Answer
A
Question: If z = x +iy, then the equation
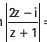
= mrepresents a circle when mis not equal to
(a)1/2
(b) 1
(c) 2
(d) 3
Answer
C
Question: If z be any complex number such that |3z – 2| + |3z + 2| = 4, then locus of z is
(a) a circle
(b) an ellipse
(c) a line segment
(d) None of these
Answer
C
Question: The region of the argand diagram defined by z – 1 + z + 1 £ 4 is
(a) interior of an ellipse
(b) exterior of an ellipse
(c) interior and boundary of an ellipse
(d) None of the abov
Answer
A
Question: A curve represented by Im(z ) k, 2 = where k is a non-zero real number is
(a) a pair of straight lines
(b) an ellipse
(c) a parabola
(d) a hyperbola
Answer
D
Question: If z +–zl +l z – –zl = 2, then z lies on
(a) a straight line
(b) a square
(c) a line
(d) None of these
Answer
B
Question: Value of i4k + i4k+1 + i4k + 2 + i4k + 3 is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
Question: If the ratio of the roots of x2 + bx + c = 0 and x2 + qx + r = 0 be the same, then
(a) r2c = b2 q
(b) r2 b = c2 q
(c) rb2 = cq2
(d) rc2 = bq2
Answer
C
Question: The square root of (7 – 24i) is
(a) ± (3 – 5i)
(b) ± (3 + 4i)
(c) ± (3 – 4i)
(d) ± (4 – 3i)
Answer
D
Question: Simplify the complex numbers given in column-I and match with column-II
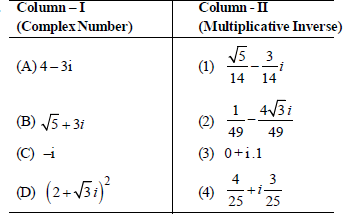
Codes:
A B C D
(a) 3 2 1 4
(b) 4 3 1 2
(c) 2 1 3 4
(d) 4 1 3 2
Answer
D
Question: If the roots of the equations px2 + 2qx + r = 0 and qx2 – 2(√pr ) x + q = 0 be real, then
(a) p = q
(b) q2 = pr
(c) p2 = qr
(d) r2 = pq
Answer
B
Question: The value of (1 + i)5 × (1 – i)5 is
(a) –8
(b) 8i
(c) 8
(d) 32
Answer
D
Question: If z1 = 6 + 3i and z2 = 2 – i, then z1/z2 is equal to 1/a (9 + 12i). The value of ‘a’ is
(a) 1
(b) 2
(c) 4
(d) 5
Answer
D
Question: If x + iy = a + ib/a – ib, then x2 + y2 =
(a) 1
(b) 2
(c) 0
(d) 4
Answer
A
Question: If the roots of the equation x2 – 2ax + a2 + a – 3 = 0 are real and less than 3, then
(a) a < 2
(b) 2 ≤ a ≤ 3
(c) 3 < a ≤ 4
(d) a > 4
Answer
D
Question: If 1 – i, is a root of the equation x2 + ax + b = 0, where a, b ∈ R, then the values of a and b are,
(a) 2, 2
(b) –2, 2
(c) –2, –2
(d) 1, 2
Answer
B
Question: The real part of (1 + i )2/(3 – i ) is
(a) 1/3
(b) 1/5
(c) – 1/3
(d) None of these
Answer
D
STATEMENT TYPE QUESTIONS
Question: Statement – I : Let z1 and z2 be two complex numbers such that z¯1 + iz¯2 = 0 and arg(z1. z2) = π, then arg(z1) is 3π/4
Statement – II : arg(z1 . z2) = arg z1 + arg z2.
(a) Statement I is correct
(b) Statement II is correct
(c) Both are correct
(d) Neither I nor II is correct
Answer
C
Question: Statement – I : If (a + ib) (c + id) (e + if ) (g + ih) = A + iB, then (a2 + b2) (c2 + d2) (e2 + f2) (g2 + h2) = A2 + B2.
Statement II : If z = x + iy, then lzl = √x2 + y2.
(a) Statement I is correct
(b) Statement II is correct
(c) Both are correct
(d) Neither I nor II is correct
Answer
C
Question: Which of the following are correct?
I. Modulus of 1 + i/1 – i is 1.
II. Argument of 1 + i/1 – i + is π/2.
III. Modulus of 1/1 + i is √2.
IV. Argument of 1/1 + i is π/4.
(a) I and II are correct
(b) III and IV are correct
(c) I, II and III are correct
(d) All are correct
Answer
A
Question: Consider the following statements.
I. The value of x3 + 7x2 – x + 16, when x = 1 + 2i is –17 + 24i.
II. If iz3 +z2 – z + i = 0 then |z| = 1
Choose the correct option.
(a) Only I is correct.
(b) Only II is correct.
(c) Both are correct.
(d) Both are incorrect.
Answer
C
Question: Consider the following statements.
I. Let z1 and z2 be two complex numbers such that |z1 + z2| = |z1| + |z2| then arg (z1) – arg (z2) = 0
II. Roots of quadratic equation x2 + 3x + 5 = 0 is x = –3 ±i√11/2
Choose the correct option.
(a) Only I is correct.
(b) Only II is correct.
(c) Both are correct.
(d) Neither I nor II is correct.
Answer
C
We hope you liked the above Complex Numbers and Quadratic Equations MCQ Class 11 Mathematics. In case you have any questions please put them in the comments
