Probability MCQ Questions Class 12 Mathematics
Please refer to MCQ Questions for Class 12 Mathematics Chapter 13 Probability with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 12 Mathematics. Students should refer to MCQ Questions for Class 12 Mathematics with Answers to score more marks in Grade 12 Mathematics exams. Students should read the chapter Probability and then attempt the following objective questions.
MCQ Questions for Class 12 Mathematics Chapter 13 Probability with answers
MCQ Questions for Class 12 Mathematics Chapter 13 provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. An instructor has a question bank consisting of 300 easy true/false questions, 200 difficult true/false question, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the test bank, what is the probability that it will be an easy question given that it is a multiple choice question?
(a) 1/9
(b) 2/9
(c) 4/9
(d) 5/9
Answer
D
Question. Consider the experiment of throwing a die, if a multiple of 3 comes up throw the die again and if any other number comes, toss a coin. The conditional probability of the event the coin shows a tail, given that at least one die shows a 3 is
(a) 0
(b) 7/20
(c) 3/20
(d) 4/5
Answer
A
Question. Assume that each child born is equally likely to be boy or a girl. If a family has two children, what is the conditional probability that both are girls given that
(i) the youngest is a girl?
(ii) at least one is a girl?
(a) 2/3 and 1/4
(b) 1/2 and 1/3
(c) 1/3 and 1/4
(d) 1/2 and 1/4
Answer
B
Question. A committee of 4 students is selected at random from a group consisting 8 boys and 4 girls. Given that there is atleast one girl on the committee, the probability that there are exactly 2 girls on the committee, is
(a) 7/99
(b) 13/99
(c) 14/99
(d) None of these
Answer
D
Question. If A and B are two events such that A ⊂ B and P (B) ≠ 0, then which of the following is correct?

Answer
C
Question. A and B are two events such that P (A)≠ 0. P (B/A) if (i) A is a subset of B (ii) A ∩ B = φ are respectively
(a) 0 and 1
(b) 1 and 0
(c) 1 and 1
(d) 0 and 0
Answer
B
Question. A laboratory blood test is 99% effective in detecting a certain disease when it is in fact present. However, the test also yields a false positive result for 0.5% of the healthy person tested (i.e., if a healthy person is tested, then with probability 0.005, the test will imply he has the disease). If 0.1% of the population actually has the disease, what is the probability that a person has disease given that his test result is positive?
(a) 11/133
(b) 22/133
(c) 33/133
(d) None of these
Answer
B
Question.

Answer
C
Question. Two events E and F are independent. If P(E) = 0.3, P(E ∪ F) = 0.5, then P(E|F) – P(F|E) equals
(A) 2/7
(B) 3/35
(C) 1/70
(D) 1/7
Answer
C
Question. If A and B are two independent events with P(A) = 3/5 and P(B) = 4/5, then P(A’ ∩ B’) equals
(A) 4/15
(B) 8/45
(C) 1/3
(D) 2/9
Answer
D
Question. If A and B are such events that P(A) > 0 and P(B) ≠ 1, then P (A|B) equals

Answer
C
Question. In answering a question on a multiple choice test a student either knows the answer or guesses. Let 3/4 be the probability that he knows the answer and 1 /4 be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability 1/4 . What is the probability that a student knows the answer given that he answered it correctly?
(a) 4 /13
(b) 5/13
(c) 9/13
(d) 12/13
Answer
D
Question. There are three coins. One is a two headed coin (having head on both faces), another is a biased coin that comes up heads 75% of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows head, what is the probability that it is was the two headed coin?
(a) 2/9
(b) 4/9
(c) 2/3
(d) 2/9
Answer
B
Question. An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of accidents are 0.01, 0.03 and 0.15, respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver?
(a) 1/52
(b) 1/26
(c) 7/52
(d) 3/26
Answer
A
Question. Three machines E1, E2 and E3 in a certain factory produce 50%, 25% and 25%, respectively, of the total daily output of electric tubes. It is known that 4% of the tubes produced one each of machines E1 and E2 are defective and that 5% of those produced on E3 are defective. If one tube is picked up at random from a day’s production, the probability that it is defective, is
(a) 0.025
(b) 0.125
(c) 0.325
(d) 0.0425
Answer
D
Question. Two groups are competing for the position on the board of directors of a corporation. The probability that the first and the second groups will win are 0.6 and 0.4, respectively. Further, if the first group wins the probability of introducing a new product is 0.7 and the corresponding probability is 0.3, if the second group wins. The probability that the new product introduce was by the second group, is
(a) 2/9
(b) 1/9
(c) 4/9
(d) 1/3
Answer
A
Question. Suppose, a girl throws a die. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1, 2, 3 or 4 she tosses a coin once and notes whether a head or tail is obtained. If she obtained exactly one head, what is the probability that she threw 1, 2, 3 or 4 with the die?
(a) 4/11
(b) 2/11
(c) 6/11
(d) 8/11
Answer
D
Question. A factory has two machines A and B. Past record shows that machine A produced 60% of the item of output and machine B produced 40% of the items.
Further, 2% of the items produced by machine A and 1% produced by machine B were defective. All the items are put into one stockpile and then one item is chosen at random from this and is found to be defective. What is the probability that it was produced by machine B?
(a) 1/2
(b) 1/4
(c) 3/4
(d) 2/3
Answer
B
Question. Probability that A speaks truth is 4/5 . A coin is tossed, A reports that a head appears. The probability that actually there was head is
(a) 4/5
(b) 1/2
(c) 1/5
(d) 2/5
Answer
A
Question. Assume that the chances of a patient having a heart attack is 40%. It is also assumed that a meditation and yoga course reduces the risk of heart attack by 30% and prescription of certain drug reduces its chances by 25%. At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options the patient selected at random suffers a heart attack. The probability that the patient followed a course of meditation and yoga, is
(a) 3/29
(b) 7/29
(c) 14/29
(d) None of these
Answer
C
Question. A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be diamonds. The probability of the lost card being a diamond.
(a) 11/50
(b) 2/25
(c) 9/50
(d) 43/50
Answer
A
Question. Suppose you have two coins which appear identical in your pocket. You know that one is fair and one is 2 headed. If you take one out, toss it and get a head, what is the probability that it was a fair coin?
(a) 1/4
(b) 1/3
(c) 1/2
(d) None of these
Answer
B
Question. A company has two plants to manufacture televisions. Plant I manufacture 70% of televisions and plant II manufacture 30%. At plant I, 80% of the televisions are rated as of standard quality and at plant II, 90% of the televisions are rated as of standard quality. A television is chosen at random and is found to be of standard quality. The probability that it has come from plant II is
(a) 17/50
(b) 27/83
(c) 3/5
(d) 9/83
Answer
B
Question. In a college, 30% students fail in physics, 25% fail in mathematics and 10% fail in both. One student is chosen at random. The probability that she fails in physics if she has failed in mathematics is
(A) 1/10
(B) 2/5
(C) 9/20
(D) 1/3
Answer
B
Question. Two cards are drawn from a well shuffled deck of 52 playing cards with replacement. The probability, that both cards are queens, is
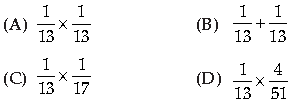
Answer
A
Question. Two dice are thrown. If it is known that the
sum of numbers on the dice was less than 6, the
probability of getting a sum 3, is
(A) 1/18
(B) 5/18
(C) 1/5
(D) 2/5
Answer
C
Question. A letter is known to have come either from TATANAGAR or from CALCUTTA. On the envelope, just two consecutive letter TA are visible.
What is the probability that the letter came from TATANAGAR?
(a) 2/11
(b) 5/11
(c) 7/11
(d) 10/11
Answer
C
Question. Let X denote the sum of the numbers obtained when two fair dice are rolled. The variance and standard deviation of X are
(a) 31/6 and √31/6
(b) 35/6 and √35/6
(c) 17/6 and √17/6
(d) None of these
Answer
B
Question. A class has 15 students whose ages are 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20 yr. One student is selected in such a manner that each has the same chance of being of chosen and the age X of the selected student is recorded. What is the probability distribution of the random variable X?
Mean, variance and Standard Deviation (SD) of X ,are respectively
(a) 17.53, 4.8 and 2.19
(b) 2.19, 4.8 and 17.53
(c) 17.53, 2.19 and 4.8
(d) None of these
Answer
A
Question. A random variable X has the following probability distribution. Then, the value of
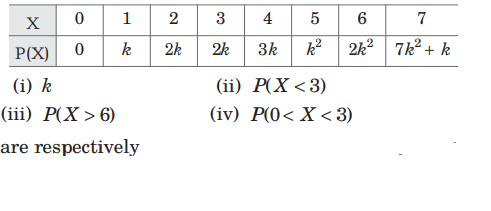
(a) 1/10, 3/10, 17/100 and 3/10
(b) 1/10, 3/10, 3/10 and 17/100
(c) 17/100, 1/10, 3/10 and 3/10
(d) None of these
Answer
A
Question. The variance and standard deviation of the number of heads in three tosses of a coin, are
(a) √3/2 and 3/4
(b) 3√4 and √3/2
(c) 4/9 and 3/2
(d) 1/2 and 1√2
Answer
C
Question. In a dice game, a player pays a stake of R.s.1 for each throw of a die. She receives R.s.5, if the die shows a 3,R.s.2, if the die shows a 1 or 6 and nothing otherwise. What is the player’s expected profit per throw over a long series of throws?
(a) 0.50
(b) 0.20
(c) 0.70
(d) 0.90
Answer
A
Question. A discrete random variable X has the following probability distribution

The value of C the mean of the distribution are
(a) 1/10 and 3.66
(b) 1/20 and 2.66
(c) 1/15 and 1.33
(d) None of these
Answer
A
Question. For a random variable X, E (X) = 3 and E (X2) = 11. Then, variable of X is
(a) 8
(b) 5
(c) 2
(d) 1
Answer
C
Question. If A and B are two events such that P(A) ≠ 0 and P(B|A) = 1, then
(A) A ⊂ B
(B) B ⊂ A
(C) B = j
(D) A = j
Answer
A
Question. If P(A|B) > P(A), then which of the following is correct:
(A) P(B|A) < P(B)
(B) P(A∩B) < P(A).P(B)
(C) P(B|A) > P(B)
(D) P(B|A) = P(B)
Answer
C
Question. If A and B are any two events such that P(A) + P(B) – P(A and B) = P(A), then
(A) P(B|A) = 1
(B) P(A|B) = 1
(C) P(B|A) = 0
(D) P(B|A) = 0
Answer
B
Question. In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is
(A) 10-1
(B) (1/2)8
(C) (9/10)5
(D) 9/10
Answer
C
Question. The probability of obtaining an even prime number on each die, when a pair of dice is rolled is
(A) 0
(B) 1/3
(C) 1/12
(D) 1/36
Answer
D
Question. If P(A) = 0.4, P(B) = 0.8 and P(B|A) = 0.6, then P(A∪B) is equal to
(A) 0.24
(B) 0.3
(C) 0.48
(D) 0.96
Answer
D
Question. Eight coins are tossed together. The probability of getting exactly 3 heads is
(A) 1/256
(B) 7/32
(C) 5/32
(D) 3/32
Answer
B
Question. A box contains 3 orange balls, 3 green balls and 2 blue balls. Three balls are drawn at random from the box without replacement. The probability of drawing 2 green balls and one blue ball is
(A) 3/28
(B) 2/21
(C) 1/28
(D) 167/168
Answer
A
Question. A and B are events such that P(A) = 0.4, P(B) = 0.3 and P(A∪B) = 0.5. Then P(B’ ∩ A’) equals
(A) 2/3
(B) 1/2
(C) 3/10
(D) 1/5
Answer
D
Question. A box has 100 pens of which 10 are defective. What is the probability that out of a sample of 5 pens drawn one by one with replacement at most one is defective?

Answer
D
Question. A and B are two students. Their chances of solving a problem correctly are 1/3 and 1/4, respectively. If the probability of their making a common error is 1/20 and they obtain the same answer, then the probability of their answer to be correct is
(A) 1/12
(B) 1/40
(C) 13/120
(D) 10/13
Answer
D
Question. 10% of the bulbs produced in a factory are of red colour and 2% are red and defective. If one bulb is picked up at random, then the probability of its being defective if it is red, is
(a) 1/5
(b) 1/3
(c) 1/4
(d) 1/2
Answer
A
Question. Two cards are drawn one by one from a pack of cards. The probability of getting first card an ace and second a coloured one is (before drawing second card first card is not placed again in the pack)
(a) 1/26
(b) 5/52
(c) 5/221
(d) 4/13
Answer
C
Question.

Answer
C
Question. If P(A) = 2/5, P(B) = 3/10 and P(A ∩ B) = 1/5, then P(A’|B’).P(B’|A’) is equal to
(A) 5/6
(B) 5/7
(C) 25/42
(D) 1
Answer
C
Question. If P(A) = 4/5 and P(A ∩ B)= 7/10, then (P(B|A) is equal to
(A) 1/10
(B) 1/8
(C) 7/8
(D) 17/20
Answer
C
Question. A die is thrown and a card is selected at random from a deck of 52 playing cards. The probability of getting an even number on the die and a spade card is
(A) 1/2
(B) 1/4
(C) 1/8
(D) 3/4
Answer
C
Question. Assume that in a family, each child is equally likely to be a boy or a girl. A family with three children is chosen at random. The probability that the eldest child is a girl given that the family has at least one girl is
(A) 1/2
(B) 1/3
(C) 2/3
(D) 4/7
Answer
D
Question. Let P(A) = = 7/13, P(B) 9/13 and P(A ∩ B) = 4/13 Then P(A’/ B) is equal to
(A) 6/13
(B) 4/13
(C) 4/9
(D) 5/9
Answer
D
Case-based MCQs
Read the following text and answer the following questions on the basis of the same:
A coach is training 3 players. He observes that the player A can hit a target 4 times in 5 shots, player B can hit 3 times in 4 shots and the player C can hit 2 times in 3 shots.

Question. Let the target is hit by A, B: the target is hit by B and, C: the target is hit by A and C. Then, the probability that A, B and, C all will hit, is
(A) 4/5
(B) 3/5
(C) 2/5
(D) 1/5
Answer
C
Question. What is the probability that B, C will hit and A will lose?
(A) 1/10
(B) 3/10
(C) 7/10
(D) 4/10
Answer
A
Question. What is the probability that ‘any two of A, B and C will hit?
(A) 1/30
(B) 11/30
(C) 17/30
(D) 13/30
Answer
D
Question. What is the probability that ‘none of them will hit the target’?
(A) 1/30
(B) 1/60
(C) 1/15
(D) 2/15
Answer
B
Question. What is the probability that at least one of A, B or C will hit the target?
(A) 59/60
(B) 2/5
(C) 3/5
(D) 1/60
Answer
A
Read the following text and answer the following questions on the basis of the same:
The reliability of a COVID PCR test is specified as follows:
of people having COVID, 90% of the test detects the disease but 10% goes undetected. Of people free of COVID, 99% of the test is judged COVID negative but 1% are diagnosed as showing COVID positive.
From a large population of which only 0.1% have COVID, one person is selected at random, given the COVID PCR test, and the pathologist reports him/her as COVID positive.

Question. What is the probability of the ‘person to be tested as COVID positive’ given that ‘he is actually having COVID’?
(A) 0.001
(B) 0.1
(C) 0.8
(D) 0.9
Answer
D
Question. What is the probability of the ‘person to be tested as COVID positive’ given that ‘he is actually not having COVID’?
(A) 0.01
(B) 0.99
(C) 0.1
(D) 0.001
Answer
A
Question. What is the probability that the ‘person is actually not having COVID’?
(A) 0.998
(B) 0.999
(C) 0.001
(D) 0.111
Answer
B
Question. What is the probability that the ‘person is actually having COVID given that ‘he is tested as COVID positive’?
(A) 0.83
(B) 0.0803
(C) 0.083
(D) 0.089
Answer
C
Question. What is the probability that the ‘person selected will be diagnosed as COVID positive’?
(A) 0.1089
(B) 0.01089
(C) 0.0189
(D) 0.189
Answer
B
Read the following text and answer the following questions on the basis of the same:
In answering a question on a multiple choice test for class XII, a student either knows the answer or guesses. Let 3/5 be the probability that he knows the answer and 2/5 be the probability that he guesses.
Assume that a student who guesses at the answer will be correct with probability 1/3. Let E1, E2, E be the events that the student knows the answer, guesses the answer and answers correctly respectively.

Question. What is the value of P(E1)?
(A) 2/5
(B) 1/3
(C) 1
(D) 3/5
Answer
D
Question. Value of P(E|E1) is
(A) 1/3
(B) 1
(C) 2/3
(D) 4/5
Answer
B
Question.
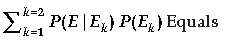
(A) 11/15
(B) 4/15
(C) 1/5
(D) 1
Answer
A
Question.
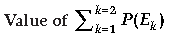
(A) 1/3
(B) 1/5
(C) 1
(D) 3/5
Answer
C
Question. What is the probability that the student knows the answer given that he answered it correctly?
(A) 2/11
(B) 5/3
(C) 9/11
(D) 13/3
Answer
C
Read the following text and answer the following questions on the basis of the same:
In an office three employees Vinay, Sonia and Iqbal process incoming copies of a certain form. Vinay process 50% of the forms. Sonia processes 20% and Iqbal the remaining 30% of the forms. Vinay has an error rate of 0.06, Sonia has an error rate of 0.04 and Iqbal has an error rate of 0.03.
Question. The conditional probability that an error is committed in processing given that Sonia processed the form is:
(A) 0.0210
(B) 0.04
(C) 0.47
(D) 0.06
Answer
B
Question. The probability that Sonia processed the form and committed an error is:
(A) 0.005
(B) 0.006
(C) 0.008
(D) 0.68
Answer
C
Question. The total probability of committing an error in processing the form is:
(A) 0
(B) 0.047
(C) 0.234
(D) 1
Answer
B
Question. The manager of the company wants to do a quality check. During inspection he selects a form at random from the days output of processed forms. If the form selected at random has an error, the probability that the form is NOT processed by Vinay is:
(A) 1
(B) 30/47
(C) 20/47
(D) 17/47
Answer
D
Question. Let A be the event of committing an error in processing the form and let E1, E2 and E3 be the events that Vinay, Sonia and Iqbal processed the form. The value of
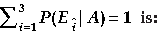
(A) 0
(B) 0.03
(C) 0.06
(D) 1
Answer
D
Read the following text and answer the following questions on the basis of the same:
A group of people start playing cards. And as we know a well shuffled pack of cards contains a total of 52 cards. Then 2 cards are drawn simultaneously (or successively without replacement).

Question. If x = no. of kings = 0, 1, 2. Then P(x = 0) = ?
(A) 188/221
(B) 198/223
(C) 197/290
(D) 187/221
Answer
A
Question. If x = no. of kings = 0, 1, 2. Then P(x = 1) = ?
(A) 32/229
(B) 32/227
(C) 32/221
(D) 32/219
Answer
C
Question. If x = no. of kings = 0, 1, 2. Then P(x = 2) = ?
(a) 2/219
(B) 1/221
(C) 3/209
(D) 1/209
Answer
B
Question. Find P(X = 1) + P(X = 2).
(A) 188/221
(B) 1/221
(C) 189/221
(D) 220/221
Answer
C
Question. Find P(x ≥ 1).
(A) 188/221
(B) 1/221
(C) 189/221
(D) 220/221
Answer
D
Read the following text and answer the following questions on the basis of the same:
Anand, Samanyu and Shah of SHORTCUTS classes were given a problem in Mathematics whose respective probabilities of solving it are 1/2, 1/3, and 1/4. They were asked to solve it independently.

Based on the above data, answer any four of the following questions.
Question. The probability that Anand alone solves it is _______.
(A) 1/4
(B) 3/4
(C) 11/24
(D) 17/24
Answer
A
Question. The probability that the problem is not solved is _______.
(A) 1/4
(B) 3/4
(C) 0
(D) 11/24
Answer
A
Question. The probability that the problem is solved is _______.
(A) 1/4
(B) 3/4
(C) 17/24
(D) 11/24
Answer
B
Question. The probability that exactly one of them solves it is _______.
(A) 1/4
(B) 3/4
(C) 17/24
(D) 11/24
Answer
D
Question. The probability that exactly two of them solves it is _______.
(A) 1/4
(B) 3/4
(C) 17/24
(D) 11/24
Answer
A
