Sequences And Series MCQ Class 11 Mathematics
Please refer to Chapter 9 Sequences And Series MCQ Class 11 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 11 Mathematics. Students should refer to MCQ Questions for Class 11 Mathematics with Answers to score more marks in Grade 11 Mathematics exams. Students should read the chapter Sequences And Series and then attempt the following objective questions.
MCQ Questions Class 11 Mathematics Chapter 9 Sequences And Series
The Sequences And Series MCQ Class 11 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. If a, b, c are in AP, then 10 a x + 10,10 bx + 10, 10c x + 10 (x ≠ 0) are in
(a) AP
(b) GP only when x > 0
(c) GP for all x
(d) GP only when x < 0
Answer
C
Question: If the altitudes of a triangle are in AP, then the sides of the triangle are in
(a) AP
(b) HP
(c) GP
(d) arithmetico-geometric progression
Answer
B
Question: In the four numbers first three are in GP and last three are in AP whose common difference is 6. If the first and last numbers are same, then first number will be
(a) 2
(b) 4
(c) 6
(d) 8
Answer
D
Question: Let n(> 1) be a positive integer, then the largest integer m such that (nm +1) divides
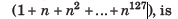
(a) 32
(b) 63
(c) 64
(d) 127
Answer
C
Question:
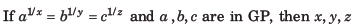
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
C
Question:
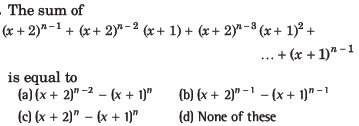
Answer
C
Question:
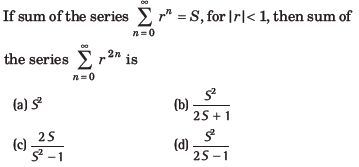
Answer
D
Question: If AM of two numbers is twice of their GM, then the ratio of greatest number to smallest number is
(a) 7 – 4 √3
(b) 7 + 4 √3
(c) 21
(d) 5
Answer
B
Question: Let two numbers have arithmetic mean 9 and geometric mean 4. Then, these numbers are the roots of the quadratic equation
(a) x2 -18x -16 = 0
(b) x2 -18x + 16 = 0
(c) x2 + 18x -16 = 0
(d) x2 + 18x +16 = 0
Answer
B
Question: An infinite GP has the first term ‘ x’ and sum 5, then x belongs to
(a) x < -10
(b) -10 < x < 0
(c) 0 < x < 10
(d) x > 10
Answer
C
Question: If ngeometric means between a and bbe G1, G2…, Gn
and a geometric mean beG, then the true relation is
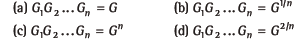
Answer
C
Question: If the 7th term of a HP is1/10and the 12th term is1/25 then the 20th term is
(a)1/41
(b)1/45
(c)1/49
(d)1/37
Answer
C
Question:
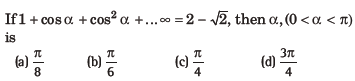
Answer
D
Question: If a, b, c, d are any four consecutive coefficients of any expanded binomial, then a+b/a ,b+c/b ,c+d/c are in
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
C
Question: If log a x, logb x, logc x be in HP, then a, b, c are in
(a) AP
(b) HP
(c) GP
(d) None of these
Answer
C
Question: The product of n positive numbers is unity. Their sum is
(a) a positive integer
(b) equal to n+1/n
(c) divisible by n
(d) never less than n
Answer
D
Question: For any odd integer n ≥1,
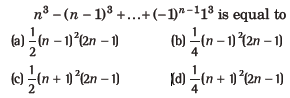
Answer
D
Question: The AM,HMandGMbetween two numbers are 144/15,15 and 12, but not necessarily in this order. Then, HM, GM and AM respectively are
(a) 15, 12,144/15
(b)144/15,, 12, 15
(c) 12, 15,144/15
(d)144/15, 15, 12
Answer
B
Question: If a, b and c are in AP and p, p’ are the AM and GM respectively between a and b, while q, q’ are the AM and GM respectively between b and c, then
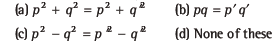
Answer
C
Question:
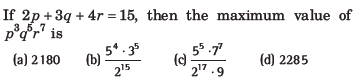
Answer
C
Question:
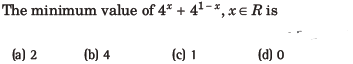
Answer
B
Question: If|x|< 1, then the sum of the series 1+2x+3x2 +4X3 + ….∞ will
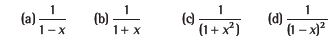
Answer
D
Question: 1+3/2+5/22+7/23..∞ is equal to
(a) 3
(b) 6
(c) 9
(d) 12
Answer
D
Question: The sum of the series 1.3.5+2.5.8+3.7.11+… upto n terms is
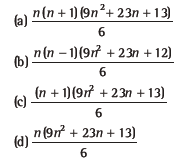
Answer
A
Question: If Tn denotes the nth term of the series
2 + 3 + 6 + 11 + 18 + . . . , then T50 is
(a) 492 – 1
(b) 492
(c) 502+1
(d) 492+2
Answer
D
Question:
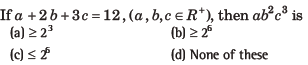
Answer
C
Question: Sumof nterms of series12 + 16 + 24 + 40 + … will be

Answer
D
Question: The sum of the series 1+3x+6x2+10x3 +∞ … will be
(a) 1/(1-x)2
(b)1/1-x
(c)1/(1+x)2
(d)1/(1-x)3
Answer
D
Question: The sum of n terms of the infinite series
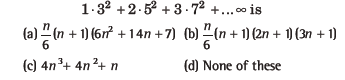
Answer
A
Question: Let Sn denote the sum of the cubes of the first n natural numbers and sn denote the sum of the first n
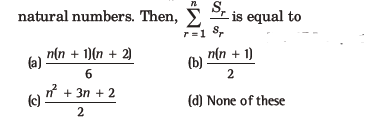
Answer
A
Question: The sum of the series 1/3×7+1/7×11+1/11×15+…is
(a)1/3
(b)1/6
(c)1/9
(d)1/12
Answer
D
Question: The nth term of the series
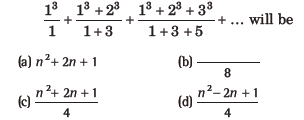
Answer
C
Question:The sum of the series
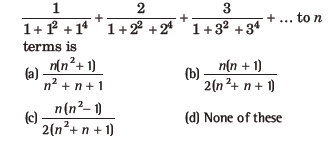
Answer
C
Question. The solution of the equation
(x + 1) + (x + 4) + (x + 7) + …+ (x + 28) = 155 is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
Question. If (1+x) (1+x2) (1+x4).…(1+x128) + ∑nr=0 , then n is equal to
(a) 255
(b) 127
(c) 60
(d) None of these
Answer
A
Question. Two numbers whose arithmetic mean is 34 and the geometric mean is 16, then the ratio of numbers is
(a) 5 or 1/5
(b) 4 or 1/4
(c) 2 or 1/2
(d) 16 or
Answer
D
Question. The sum of all two digit numbers which, when divided by 4, yield unity as a remainder is
(a) 1190
(b) 1197
(c) 1210
(d) None of these
Answer
C
Question. The sum of integers from 1 to 100 that are divisible by 2 or 5 is
(a) 3000
(b) 3050
(c) 4050
(d) None of these
Answer
B
Question. The sum of the integers from 1 to 100 which are not divisible by 3 or 5 is
(a) 2489
(b) 4735
(c) 2317
(d) 2632
Answer
C
Question. The number 111…1 (91 times) is a/an
(a) even number
(b) prime number
(c) not prime
(d) None of these
Answer
C
Question. Let n(>1) be a positive integer, then the largest integer m such that (n ) m + 1 divides
(1 … ) + n + n2 + + n127 , is
(a) 32
(b) 63
(c) 64
(d) 127
Answer
C
Question. If a, b, c are in GP and log a – log 2 b, log 2 b – log 3c andlog 3c – log a are in AP, then a, b, c are the length of the sides of a triangle which is
(a) acute angled
(b) obtuse angled
(c) right angled
(d) equilateral
Answer
B
Question. Find four numbers forming a GP in which the third term is greater than the first term by 9 and the second term is greater than 4th by 18.
(a) 2, –6, 12, –24
(b) 3, 6, 12, 24
(c) 3, –6, 12, –24
(d) None of these
Answer
C
Question. The number which should be added to the numbers 2, 14, 62, so that the resulting numbers may be in GP, is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
Question. If the pth, q th, r th terms of a GP are a, b and c respectively, then aq – r br – p c p – q is equal to
(a) 0
(b) 2
(c) 1
(d) 4
Answer
C
Question. If a, b, c and d are in GP, then
(a2 + b2 + c2 )(b2 + c2 + d2 ) is equal to
(a) (ab + bc + cd)2
(b) (ab – bc – cd)2
(c) (ab + bc + cd)
(d) None of these
Answer
A
Question. The third term of GP is 4. The product of its first 5 terms is
(a) 43
(b) 44
(c) 45
(d) None of these
Answer
C
Question. If the arithmetic mean of a and b is an + bn /an-1 + bn-1 ,then the value of n is
(a) -1
(b) 0
(c) 1
(d) None of these
Answer
C
Question. Sum of the first p, q and r terms of an AP are a, b and c respectively. Then, a/p(q-r) + b/p(r-p) + c/r(p – q) is equal to
(a) pq
(b) 0
(c) rp
(d) 3
Answer
B
Question. If x, 2y and 3 z are in AP, where the distinct numbers x, y, zare in GP, then the common ratio of the GP is
(a) 3
(b) 1/3
(c) 2
(d) 1/2
Answer
B
Question. The length of three unequal edges of a rectangular solid block are in GP. The volume of the block is 216 cm3 and the total surface area is 252 cm2. The length of the longest edge is
(a) 12 cm
(b) 6 cm
(c) 18 cm
(d) 3 cm
Answer
A
Question. If a, b, c and d are in GP, then an + bn , bn + cn , cn + dn are in
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
B
Question. If A is the arithmetic mean and G1 , G2 , be two geometric means between any two numbers, then G12/G2 + G22/G1 is equal to
(a) 2A
(b) A
(c) 3A
(d) None of these
Answer
Question. If a, b, c, dand pare different real numbers such that
(a2 + b2 + c2 ) p2-2(ab + bc + cd)p + (b2 + c2 + d2 ) ≤0, then a, b, c, d are in
(a) AP
(b) GP
(c) HP
(d) ab = cd
Answer
A
Question. The sum of nterms of three AP’s whose first term is 1 and common differences are 1, 2, 3 respectively are S1, S2 , S3 respectively. The true relation is
(a) S1 + S3 = S2
(b) S1 + S3 = 2 S2
(c) S1 + S2 = 2 S3
(d) S1 + S2 = S3
Answer
B
Question. If the first term of an AP is a and the sum of the first p terms is zero, then the sum of its next q terms is
(a) a(p + q)q / p-1
(b) -a (p + q)q/p-1
(c) a(p – q) q/ p – 1
(d) None of these
Answer
B
Question. (666..6)2 + (888…8) is equal to
(a) 4/9 (10n – 1)
(b) 4/9 (10n – 1 )
(c) 1-(1/10)106
(d) None of these
Answer
B
Question. If a2 , b2 , c2 , , are in AP, then which of the following is also in AP ?
(a) sin A, sin B, sinC
(b) tan A, tan B, tanC
(c) cot A, cot B, cot C
(d) None of these
Answer
C
Question. Insert three arithmetic means between 3 and 19
(a) 6, 10, 14
(b) 7, 11, 15
(c) 8, 12, 16
(d) None of these
Answer
B
Question. The value of 0.23&4& is
(a) 232/990
(b) 232/9990
(c) 232/900
(d) 232/9909
Answer
A
Question. 0.14189189189 … can be expressed as a rational number
(a) 7/3700
(b) 7/50
(c) 525/111
(d) 21/148
Answer
D
Question. The sum of the geometric progression 0.15, 0.015, 0.0015, … 20 terms is
(a) 1/6[1 – (0.1)20]
(b) [1 – (0.1)20]
(c) 1/6[1 – (0.1)20]
(d) None of these
Answer
A
Question. If x > 1, y > 1, z > 1are in GP, then 1/1+ logx , 1 + log y , 1/1 + log z are in
(a) AP
(b) HP
(c) GP
(d) None of these
Answer
B
Question. If a, b, c be in GP, then log a , log b , log c n n n will be
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
A
Question. If 1 + λ + λ2 + + λn = (1 + λ) (1 + λ2) (1 + λ4) (1 + λ) (1 + λ8) (1 + λ16) then the value of n is (where n Î N)
(a) 32
(b) 16
(c) 31
(d) 15
Answer
C
Question. If x,1, zare in AP and x,2, zare in GP, then x, 4, zwill be in
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
C
Question. In the four numbers first three are in GP and last three are in AP whose common difference is 6. If the first and last numbers are same, then first number
will be
(a) 2
(b) 4
(c) 6
(d) 8
Answer
D
Question. If a b c 1/ x = 1/ y = 1/ z and a, b, c are in GP, then x, y, z will be in
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
A
Question. In a GP the sum of three numbers is 14, if 1 is added to first two numbers and subtracted from third number the series becomes AP, then the greatest number is
(a) 8
(b) 4
(c) 24
(d) 16
Answer
A
Question. Which of the following statement is correct ?
(a) If each term of an AP a number is added or subtracted,then the series so obtained is also an AP.
(b) The nth term of geometric series whose first term is a and common ratio r, is ar n -1.
(c) If each term of a GP be raised to the same power the resulting terms are in GP.
(d) All of the above
Answer
D
Question. Three numbers form a GP. If the 3rd term is decreased by 64, then the three numbers thus obtained will constitute an AP. If the second term of this AP is decreased by 8, a GP will be formed again, then the numbers will be
(a) 4, 20, 36
(b) 4, 12, 36
(c) 4, 20, 100
(d) None of these
Answer
C
Question. If AM of two numbers is twice of their GM, then the ratio of greatest number to smallest number is
(a) 7 – 4√3
(b) 7 + 4√3
(c) 21
(d) 5
Answer
B
Question. An infinite GP has the first term ‘ x’ and sum 5, then x belongs to
(a) x < -10
(b) -10 < x < 0
(c) 0 < x < 10
(d) x > 10
Answer
C

We hope you liked the above Sequences And Series MCQ Class 11 Mathematics. In case you have any questions please put them in the comments box below and our teachers will provide you a response.
