Please refer to Chapter 13 Statistics MCQ Class 10 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 10 Mathematics. Students should refer to MCQ Questions for Class 10 Mathematics with Answers to score more marks in Grade 10 Mathematics exams. Students should read the chapter Statistics and then attempt the following objective questions.

MCQ Questions Class 10 Mathematics Chapter 13 Statistics

The Statistics MCQ Class 10 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.

Question. Find the mean of the following frequency distribution.

(a) 25. 3
(b) 25.2
(c) 24
(d) 25.5

Question. The mean of 15 observations written in some order is 50. If the mean of first eight observations and last eight observations are 48 and 53 respectively, then the eighth observation is
(a) 35
(b) 80
(c) 72
(d) 58

Question. Calculate the mean of the following frequency distribution:

(a) 195.5
(b) 198.8
(c) 196.8
(d) 195

Question. If the mean of first ‘n’ odd natural numbers is ‘n’ itself, what is the value of ‘n’?
(a) 2
(b) 3
(c) 1
(d) Any natural number

Question. The mean of 5 observation is 15. If the mean of first three observations is 14 and last three observations is 17, then the third observation is :
(a) 18
(b) 19
(c) 17
(d) 20

Question. What is the arithmetic mean of 20 fours, 40 fives, 30 sixes and 10 tens?
(a) 50
(b) 25
(c) 5.6
(d) 33

Question. If the mean of the numbers 27 + x, 31 + x, 89 + x, 107 + x, 156 + x is 82, then the mean of 130 + x, 126 + x, 68 + x, 50 + x, 1 + x is
(a) 75
(b) 157
(c) 82
(d) 80

Question. If the class-intervals are 10 – 19, 20 – 29, 30 – 39, ………….., then the upper limit of the first class-interval is
(a) 19.5
(b) 19
(c) 20
(d) None of these

Question. There are three sections A, B and C in class X with 25, 40 and 35 students respectively. The average marks obtained by section A, B and C are 70%, 65% and 50% respectively. Find the average marks of entire class X.
(a) 59%
(b) 56%
(c) 63%
(d) 61%

Question. In the following distribution the number of families having income range (in `₹) 16000 – 19000 is

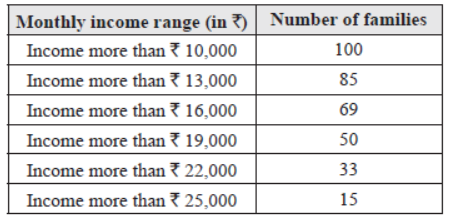
(a) 15
(b) 16
(c) 17
(d) 19

Question. The numbers 3, 5, 7 and 9 have their respective frequencies x – 2, x + 2 , x – 3 and x + 3. If the arithmetic mean is 6.5, then the value of x is
(a) 3
(b) 4
(c) 5
(d) 6

Question. If the mean of the observations x, x + 3, x + 5, x + 7 and x + 10 is 9, then the mean of the last three observations is
(a) 10, 1/ 3
(b) 10, 2/ 3
(c) 11,1/ 3
(d) 11,2/ 3

Question. Positive integers from 1 to 21 are arranged in 3 groups of 7 integers each, in some particular order. Then the highest possible mean of the medians of these 3 groups is ______
(a) 16
(b) 12.5
(c) 11
(d) 14

Question. The median of a set of 9 distinct observations is 20.5. If each of the largest 4 observation of the set is increased by 2, then the median of the new set
(a) is increased by 2
(b) is decreased by 2
(c) is two times the original median
(d) remains the same as that of the original set

Question. The mean weight of a class of 35 students is 45kg. If the weight of a teacher be included, the mean weight increases by 500 grams. Find the weight of the teacher.
(a) 63 kg
(b) 61 kg
(c) 64 kg
(d) 70 kg

Question. A set of numbers consists of three 4’s, five 5’s, six 6’s, eight 8’s and seven 10’s. The mode of this set of numbers is
(a) 6
(b) 7
(c) 8
(d) 10

Question. Let x₁, x₂ , …, x₁₁ be 11 distinct positive integers. If we replace the largest of these integers by the median of the other 10 integers, then
(a) the median remains the same
(b) the mean increases
(c) the median decreases
(d) the mean remains the same

Question. The mean of a set of 20 observation is 19.3. The mean is reduced by 0.5 when a new observation is added to the set. The new observation is
(a) 19.8
(b) 8.8
(c) 9.5
(d) 30.8

Question. The mean of fifteen different natural numbers is 13. The maximum value for the second largest of these numbers is
(a) 46
(b) 51
(c) 52
(d) 53

Question. For the data (2, 9, x + 6, 2x + 3, 5, 10, 5) if mean is 7, then mode is
(a) 3
(b) 5
(c) 9
(d) 10

Question. In a frequency distribution, the mid value of a class is 10 and the width of the class is 6. The lower limit of the class is
(a) 6
(b) 7
(c) 8
(d) 12

Question. The mean of three positive numbers is 10 more than the smallest of the numbers and 15 less than the largest of the three. If the median of the three numbers is 5, then the mean of squares of the numbers is
(a) 108, 2 /3
(b) 116, 2 /3
(c) 208,1/ 3
(d) 216, 2/ 3

Question. For the following grouped frequency distribution 1 Consider the following.

(I) Lower limit of model class is 12
(II) Frequency of the class preceding the model class=10
(III) Mode = 14.6
(IV) Width of the model class is 4 Which of the following is correct? 
(a) I and II
(b) II and III
(c) I, II and III
(d) All of these

Question. The mean of a group of eleven consecutive natural numbers is m. What will be the percentage change in the mean when next six consecutive natural numbers are included in the group ?
(a) m%
(b) m/3 %
(c) m/300 %
(d) 300 / m %

Question. The marks in science of 80 students of class X are given below. Find the mode of these marks obtained by the students in science.

(a) 53.18
(b) 53.25
(c) 52.25
(d) 53

Question. A 100 mark examination was administered to a class of 50 students. Despite only integer marks being given, the average score of the class was 47.5. Then, the maximum number of students who could get marks more than the class average is
(a) 25
(b) 35
(c) 45
(d) 49

Fill in the Blanks :

Question. The mid-value of 20-30 is ……………..

Question. Median divides the total frequency into ………. equal parts.

Question. The sum of 12 observations is 600, then their mean is ………

Question. A class interval of a data has 15 as the lower limit and 25 as the size, then the class mark is ………….

Question. Two ogives, for the same data intersect at the point P. Then, Y-coordinate of P represents ……………… .

Question. The …………….. is the most frequently occurring observation.

Question. The algebraic sum of the deviations from arithmetic mean is always ……………

Question. Facts or figures, collected with a definite purpose, are called . ……………..

Question. 0–10, 10–20, 20–30 ………… so on are the classes, the lower boundary of the class 20–30 is ……………

Question. Value of the middle-most observation (s) is called …………

Question. In the class interval 35-46, the lower limit is ……. and upper limit is ………….

Question. The class mark of a class is 25 and if the upper limit of that class is 40, then its lower limit is ……………….

Question. To find the mode of a grouped data, the size of the classes is ………………

Question. The mid-point of a class interval is called its …………….

Question. On an ogive, point A (say), whose Y- co-ordinate is n/2 (half of the total observation), has its X-coordinate equal to ……………… of the data.

Question. 3 median = mode + …………. mean.

True Or False :

Question. 2(Median – Mean) = Mode – Mean.

Question. If 16 observations are arranged in ascending order, then median is (8th observation + 9th observation)/2

Question. Mean may or may not be the appropriate measure of central tendency.

Question. Mode of 2, 3, 4, 5, 0, 1, 3, 3, 4, 3 is 3.

Question. The median of grouped data with unequal class sizes cannot be calculated.

Question. Mean of 41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 49, 42, 52, 60 is 55.4

Question. Class mark = Upper class limit + Lower class limit / 2 .

Question. The mean of x, y, z is y, then x + z = 2y.

Question. Median of 15, 28, 72, 56, 44, 32, 31, 43 and 51 is 43.

Question. The modal value is the value of the variate which divides the total frequency into two equal parts.

Match the Following :

Question. The table shows a frequency distribution of the life time of 400 radio tubes tested at a company.

Column-II gives data for description given in Column-I, match them correctly.

Question. Following is the distribution of heights of students in a class and the total number of students is 50.

With the help of information given match the columns.

Question.

Question .For the following marks distribution of 5 students in an examination, match Column-I with the data given in Column- II.

Here,
x_k = lower limit of the modal class interval
h = width of the class interval
f_k = frequency of the modal class
f_k–1 = frequency of the class preceding the modal class
f_k+1 = frequency of the class succeeding the modal class

Column-I	Column-II
(A) xk	(p) 3
(B) fk	(q) 10
(C) fk–1	(r) 0
(D) h	(d) 1

Question. For the given frequency distribution, match the Column-I with Column-II.

h = width of the class interval
c = cumulative frequency
f = frequency of the class interval to which median belongs
l₁ = lower limit of the median class interval

Column-I	Column-II
(A) f	(p) 45.4
(B) c	(q) 45
(C) l1	(r) 48
(D) median	(s) 23

We hope you liked the above Statistics MCQ Class 10 Mathematics. In case you have any questions please put them in the comments box below and our teachers will provide you a response.