Statistics MCQ Class 11 Mathematics
Please refer to Chapter 15 Statistics MCQ Class 11 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 11 Mathematics. Students should refer to MCQ Questions for Class 11 Mathematics with Answers to score more marks in Grade 11 Mathematics exams. Students should read the chapter Statistics and then attempt the following objective questions.
MCQ Questions Class 11 Mathematics Chapter 15 Statistics
The Statistics MCQ Class 11 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. The weighted mean of first n natural numbers whose weights are equal to the squares of corresponding numbers is
(a) n+1/2
(b) 3(n+1)/(2(2n+1)
(c) (n+1)/(2n+1)
(d) n(n+1)/2
Answer
B
Question: If the mean of n observations 12,22,,32,…,n2 is 46n/11 then n is equal to
(a) 11
(b) 12
(c) 23
(d) 22
Answer
A
Question: The AM of the series 1, 2, 4, 8, 16, …, 2n is
(a) 2n-1/n
(b) 2n+1 -1/n+1
(c) 2n+1/n
(d) 2n-1/n+1 1
Answer
B
Question: If X̅1 and x̅2 are the means of two distributions such that x̅1<x̅ 2x and x̅ is the mean of the combined distribution, then
(a) x̅ < x̅1
(b) x̅ > x̅2
(c) x̅ = x̅1 + x̅2/2
(d) x̅1 < x̅ < x̅2
Answer
D
Question: In a class of 50 students, 10 have failed and their average marks are 28. The total marks obtained by the entire class are 2800. The average marks of those who have passed, are
(a) 43
(b) 53
(c) 63
(d) 70
Answer
C
Question: The mean of 30 given numbers, when it is given that the mean of 10 of them is 12 and the mean of the remaining 20 is 9, is equal to
(a) 11
(b) 10
(c) 9
(d) 5
Answer
B
Question: The mean of n observations is x. If one observation xn + 1 is added, then the mean remains same. The value of xn + is
a) 0
(b) 1
(c) n
(d) x
Answer
D
Question: Mean of 100 observations is 45. If it was later found that two observations 19 and 31 were incorrectly recorded as 91 and 13. The correct mean is
(a) 44
(b) 45
(c) 44.46
(d) 45.54
Answer
C
Question: If the mean of the set of numbers x1,x2,…, xn is x̅, then the mean of the numbers xi + 2i, 1 ≤ i ≤ n is
(a) x̅ + 2n
(b) x̅ + n +1
(c) x̅ + 2
(d) x̅ + n
Answer
B
Question: In a class of 100 students, the average amount of pocket money is R.s. 35 per student. If the average is R.s. 25 for girls and R.s. 50 for boys, then the number of girls in the class is
(a) 20
(b) 40
(c) 60
(d) 80
Answer
C
Question: The mean of a set of observations is X̅. If each observation is divided by, α ≠ 0 and then is increased by 10, then the mean of the new set is
(a) x̅/α
(b) x̅ + 10/α
(c) x̅ + 10 α/α
(d) α x̅ + 10
Answer
C
Question: If a variate x is expressed as a linear function of two variates u and v in the form x=au + bv, then mean X̅
of x is
(a) au̅ + bv̅
(b) u̅ + v̅
(c) b̅ u + a̅ v
(d) None of these
Answer
A
Question: The average salary of male employees in a firm was R.s.520 and that of females wasr Rs. 420. The mean salary of all the employees was Rs.500. The percentage of male employees is
(a) 80%
(b) 60%
(c) 40%
(d) 20%
Answer
A
Question: If the sum of deviations of a number of observations about 4 is 30 and that about 3 is 40. Then, mean of the observations is
(a) 7
(b) 10
(c) 11
(d) None of these
Answer
A
Question. If the mean of the numbers 27 + x, 31+ x, 89 + x, 107 + x, 156 + x is 82, then the mean of 130 + x, 126 + x, 68 + x, 50 + x, 1+ x is
(a) 75
(b) 157
(c) 82
(d) 80
Answer
A
Question. If a variable take values 0, 1, 2, …,n with frequencies qn , n/1 qn-1 p, n(n-1)/1.2 qn-2p2,……pn wherep + q = 1, then themean is
(a) np
(b) nq
(c) n (p + q)
(d) None of these
Answer
A
Question. Let s be the standard deviation of n observations. Each of the n observations is multiplied by a constant c. Then, the standard deviation of the resulting number is
(a) s
(b) cs
(c) s c
(d) None of these
Answer
B
Question. The mean deviation from the mean of the AP
(a) n (n + 1)d
(b) n (n + 1)d /2n+1
(c) n (n + 1)d/2n
(d) n (n + 1)d/2n + 1
Answer
B
Question. The variance of 6, 8, 10, 12, 14 is
(a) 7
(b) 8
(c) 12
(d) 16
Answer
B
Question . The mean and standard deviation of six observations are 8 and 4, respectively. If each observation is multiplied by 3, then find the mean and new standard deviation of the resulting observations.
(a) 24, 12
(b) 24,144
(c) 24, 150
(d) 12, 12
Answer
A
8. The sum and sum of squares corresponding to length x (in cm) and weight (y) (in g) of 50 plant products are given below
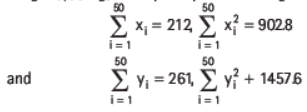
Which is more varying, the length or weight?
(a) weight
(b) length
(c) cannot be determined
(d) None of these
Answer
A
Question. A statistical measure which cannot be determined graphically is
(a) median
(b) mode
(c) harmonic mean
(d) mean
Answer
C
Question. The arithmetic mean of an AP and the mean of first and last term of an AP are
(a) equal
(b) unequal
(c) square of each other
(d) None of the above
Answer
A
Question. Mean of 100 items is 49. It was discovered that three items which should have been 60, 70 and 80 were wrongly read as 40, 20 and 50, respectively. The correct mean is
(a) 48
(b) 82(1/2)
(c) 50
(d) 80
Answer
C
Question. The AM of n numbers of a series is x. If the sum of first (n – 1) terms is k, then the nth number is
(a) x – k
(b) nx – k
(c) x – nk
(d) nx – nk
Answer
B
Question. If the average of the numbers 148, 146, 144, 142, …in AP, be 125, then the total numbers in the series will be
(a) 18
(b) 24
(c) 30
(d) 48
Answer
B
Question. The mean of the values of 1, 2, 3, …, n with respectively frequencies x, 2x, 3x, …, nx is
(a) n/2
(b) 1/3 (2n + 1)
(c) 1/6 (2n + 1)
(d) n/2
Answer
B
Question. The mean age of a combined group of men and women is 25 yr. If the mean age of the group of men is 26 yr and that of the group of women is 21 yr, then the percentage of men and women in the group are respectively
(a) 60, 40
(b) 80, 20
(c) 20, 80
(d) 40, 60
Answer
B
29.
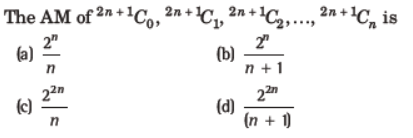
Answer
D
Question. The mean of the values 0, 1, 2, 3, …, n with the corresponding weights nC0 , nC1….nCn respectively is
(a) 2n/(n+1)
(b) 2n+1/n(n+1)
(c) (n+1)/2
(d) n/2
Answer
D
Question. The mean of nitems is x. If the first term is increased by 1, second by 2 and so on, then the new mean is
(a) x̄ + n
(b) x̄ + n/2
(c) x̄ + n+1/2
(d) None of these
Answer
C
Question. If the mean of n observations 12, 22 , 32 …, n is 46n/11 , then n is equal to
(a) 11
(b) 12
(c) 23
(d) 22
Answer
A
Question. The weighted AM of first n natural numbers whose weights are equal to the corresponding numbers is equal to
(a) 2n + 1
(b) 1/2 (2n + 1)
(c) 1/3 (2n + 1)
(d) 2n + 1/6
Answer
C
Question. The AM of the series 1, 2, 4, 8, 16, …, 2n is
(a) 2n – 1/n
(b) 2n+1 – 1/n+1
(c) 2n+1 /n
(d) 2n-1 /n+1
Answer
B
Question. Two possible observations have arithmetic mean 3 and geometric mean 2√2. If each observation is multiplied by 2, then harmonic mean will be
(a) 16/3
(b) 8/3
(c) 12
(d) None of these
Answer
A
Question. Geometric mean of first group of 5 observations is 8 and that of second group of 4 observations is 128 2.
Then, grouped geometric mean is
(a) 64
(b) 32√2
(c) 32
(d) None of these
Answer
C
Question. In a class of 50 students, 10 have failed and their average marks are 28. The total marks obtained by the entire class are 2800. The average marks of those who have passed, are
(a) 43
(b) 53
(c) 63
(d) 70
Answer
C
Question. If x̄1 and x̄2 are the means of two distributions such that x̄1 < x̄2 and x̄ is the mean of the combined distribution, then
(a) x̄ < x̄1
(b) x̄ > x̄2
(c) x̄= x̄1+x̄2 /2
(d) x̄1 < x̄ <x̄2
Answer
D
Question. If the mean of the set of numbers x1 x2 . . . xn, is x, then the mean of the numbers xi + 2i ,1 ≤ i ≤ is
(a) x̄ + 2n
(b) x̄ + n + 1
(c) x̄ + 2
(d) x̄ + n
Answer
B
Question. The mean of 30 given numbers, when it is given that the mean of 10 of them is 12 and the mean of the remaining 20 is 9, is equal to
(a) 11
(b) 10
(c) 9
(d) 5
Answer
B
Question. Mean of 100 observations is 45. If it was later found that two observations 19 and 31 were incorrectly recorded as 91 and 13. The correct mean is
(a) 44
(b) 45
(c) 44.46
(d) 45.54
Answer
C
Question. The mean of a set of observations is x. If each observation is divided by,α ≠ 0and then is increased by 10, then the mean of the new set is
(a) x̄/α
(b) x̄+10 /α
(c) x̄+10α /α
(d) αx̄+10
Answer
C
Question. If the sum of deviations of a number of observations about 4 is 30 and that about 3 is 40. Then, mean of the observations is
(a) 7
(b) 10
(c) 11
(d) None of these
Answer
A
Question. If a variate x is expressed as a linear function of two variates u and v in the form x̄= au + bv, then mean x̄ of x is
(a) aū + bv
(b) ū + v
(c) b̅u + a̅v
(d) None of these
Answer
A
Question. The average salary of male employees in a firm was ₹520 and that of females was ₹420. The mean salary of all the employees was ₹500. The percentage of male employees is
(a) 80%
(b) 60%
(c) 40%
(d) 20%
Answer
A
Question. The AM of n observations is M. If the sum of (n – 4) observations is a, then the mean of remaining four observations is
(a) nM – a/4
(b) nM + a/4
(c) nM – a/2
(d) nM + a
Answer
A
Question. The mean of the n observations x1 , x2 , x3 …xn, be x. Then, the mean of n observations 2x1+3 , 2x2 +3, 2x3 + 3, 2xn +3 is
(a) 3x̄ + 2
(b) 2x̄ + 3
(c) x̄ + 3
(d) 2x̄
Answer
B
Question. The mean deviation from the median is
(a) greater than the measured from any other value
(b) less than that measured from any other value
(c) equal to that measured from any other value
(d) maximum if all observations are positive
Answer
B
Question. Mean of 100 items is 49. It was discovered that three items which should have been 60, 70, 80 were wrongly read as 40, 20 and 50, respectively. The correct mean is
(a) 48
(b) 82.5
(c) 50
(d) 80
Answer
C
Question. If a variable takes values 0, 1, 2, …, n with frequencies qn,n/1 qn-1 p, n(n-1)/1.2 qn-2 p2 , .. . pn , where p + q = 1, then the mean is
(a) np
(b) nq
(c) n(p + q)
(d) None of these
Answer
A
Question. The GM of the numbers 2 ,22, 23 . . . 2n is
(a) 22/n
(b) 2n/2
(c) 2n-1/2
(d) 2n+1/2
Answer
D
Question. If the observations 2, 4, 8 and 16 occur 8, 6, 4 and 2 times respectively, then the geometric mean of the observations is
(a) 8
(b) 4√2
(c) 4
(d) None of these
Answer
C
Question. The mean of the series x1x2 , . . . xn, is x̄. If x2 is replaced by l, then the new mean is
(a) x̄ -x2 + λ
(b) x̄ -x2 + λ / n
(c) (n-1)x̄ +λ / n
(d) (nx̄- x2 +λ / n
Answer
D
8. For a certain frequency table which has been partly reproduced here, the arithmetic mean was found to be ₹28.07. (Diagram)
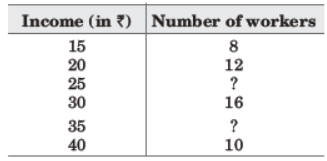
If the total number of workers is 75, then missing frequencies are respectively
(a) 14, 15
(b) 15, 14
(c) 13, 16
(d) 12, 17
Answer
B
Question. The harmonic mean of the numbers 1, 1/2 , 1/3,……,1/n is
(a) 1/n+1
(b) 2/n+1
(c) 3/n+1
(d) None of these
Answer
B
Question. If harmonic mean of first 5 observations is 5/2 and harmonic mean of another 5 observations is 9/2 , then harmonic mean of all 10 observations is
(a) 7
(b) 45/14
(c) 101/36
(d) None of these
Answer
B
Question. The quartile deviation for the following data is (diagram)

(a) 0
(b) 1/4
(c) 1/2
(d) 1
Answer
D
Question. Geometric mean of 10 observations is 8. If geometric mean of first six observations is 4, then geometric mean of last four observations is
(a) 16√2
(b) 8 2
(c) 16
(d) None of these
Answer
A
Question. If for a distribution ∑(x – 5) = 3, ∑(x – 5)2 = 43 and the total number of items is 18, find the mean and standard deviation.
(a) 94, 1.53
(b) 93, 1.53
(c) 93, 1.55
(d) None of the above
Answer
B
Question. The mean and variance of n values of a variable x are 0 and σ2, respectively. If the variable y = x2, then mean of y is
(a) σ
(b) σ2
(c) 1
(d) None of these
Answer
B
Question. Which of the following is not a measure of central tendency?
(a) Mean
(b) Median
(c) Mean-deviation
(d) Mode
Answer
C
Question. For dealing with qualitative data the best average is
(a) AM
(b) GM
(c) median
(d) mode
Answer
C
Question. The mean weight of 9 items is 15. If one more item is added to the series, the mean becomes 16. The value of 10th item is
(a) 35
(b) 30
(c) 25
(d) 20
Answer
C

We hope you liked the above Statistics MCQ Class 11 Mathematics. In case you have any questions please put them in the comments box below and our teachers will provide you a response.
