Linear Equations MCQ Class 10 Mathematics
Please refer to Chapter 3 Linear Equations MCQ Class 10 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 10 Mathematics. Students should refer to MCQ Questions for Class 10 Mathematics with Answers to score more marks in Grade 10 Mathematics exams. Students should read the chapter Linear Equations and then attempt the following objective questions.
MCQ Questions Class 10 Mathematics Chapter 3 Linear Equations
The Linear Equations MCQ Class 10 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. The value of k for which the pair of equation kx – y = 2 and 6x – 2y = 3 has unique solution
(a) k = 3
(b) k ≠ 3
(c) k ≠ 0
(d) k = 0
Answer
B
Question. Consider the equations as shown:
9x + 6y = 5
3x + 2y = 7
Which of these is true about the given equations?
(a) This is a pair of coincident lines as a1/a2=b1/b2=c1/c2 .
(b) This is a pair of parallel lines as a1/a2=b1/b2≠c1/c2.
(c) This is a pair of Intersecting lines as a1/a2=b1/b2.
(d) This is a pair of coincident lines as a1/a2=b1/b2.
Answer
B
Question. The pair of linear equations x = 0 and x = – 4 has
(a) a unique solution
(b) no solution
(c) infinitely many solutions
(d) only solution (0, 0)
Answer
B
Question. The pair of linear equations y = 0 and y = – 6 has
(a) a unique solution
(b) no solution
(c) infinitely many solutions
(d) only solution (0, 0)
Answer
B
Question. The value of k, for which the pair of linear equations kx + y = k2 and x + ky = 1 have infinitely many solutions is
(a) ±1
(b) 1
(c) –1
(d) 2
Answer
B
Question. The value of k for which the system of linear equations x + 2y = 3, 5x + ky + 7 = 0 is inconsistent is
(a) –14/3
(b) 2/3
(c) 5
(d) 10
Answer
D
Question. Consider a pair of equations as shown.
7/x+2+2/y-2=33/20
2/x+2+6/y-2=23/20
Which of these pair of equations is equivalent to the given pair of equations?
(a) 7u + 2v=33/20 and 2u +6v =23/20
(b) 7u + 6v=33/20 and 2u +2v =23/20
(c) 7u +2v =33/20 and 2u +6v =20/23
(d) 2u +6v =33/20 and 7u +2v= 23/20
Answer
A
Question. The value of k for which the system of equations x + y – 4 = 0 and 2x + ky = 3, has no solution, is
(a) – 2
(b) ≠ 2
(c) 3
(d) 2
Answer
D
Question. Consider a pair of equations as shown.
5/x+2+ 7/y+2= 31/ 12
4/x+2+3/y+2=17/12
What is the value of x and y?
(a) x = 2 and y = 4
(b) x = 3 and y = 4
(c) x = 4 and y = 2
(d) x = 4 and y = 3
Answer
C
Question. If the lines given by 3x + 2ky = 8 and 2x + 5y – 4 = 0 are parallel, then the value of k is
(a) –5/4
(b) 15/4
(c) 2/5
(d) 3/2
Answer
B
Question. If the lines given by 3 x + 2 ky = 2 and 2x + 5y + 1 = 0 are parallel, then value of k is
(a) – 5/4
(b) 2/5
(c) 15/4
(d) 3/2
Answer
C
Question. The value of k for which the system of equations x + 2y – 3 = 0 and 5x + ky + 7 = 0 has no solution, is
(a) 5
(b) 10
(c) 7
(d) None of these
Answer
B
Question. The value of k for which the lines represented by the following pair of linear equations are coincident is
2x + 3y + 7 = 0
8x + 12y + k = 0
(a) all real values except 14
(b) 8
(c) 28
(d) 14
Answer
C
Question. Consider the equations shown: ax + by = ab & 2ax + 3by = 3b Which of these is the value of y in terms of a?
(a) y = 5 − 3a
(b) y = 3 – 2a
(c) y = 9a − 35
(d) y = 2ab − 3b
Answer
B
Question. If am ≠ bl, then the system of equations, ax + by = c, lx + my = n
(a) has a unique solution
(b) has no solution
(c) has infinitely many solutions
(d) may or may not have a solution
Answer
A
Question. Consider the equations shown. p + q = 5 & p − q = 2. Which of these are the values of p and q?
(a) p = 1.5, q = 3.5
(b) p = 3.5, q = 1.5
(c) p = 2, q = 3
(d) p = 3, q = 2
Answer
B
Question. Consider the equations as shown:
(x –a )(y –b ) = (x –2a ) (y-b/2 )
x (x+1/2b)+ y(y+a/2) -2xy=5+(x-y)2
On comparing the coefficients, a student says these pairs of equations is consistent. Is he/she correct? Which of these explains why?
(a) Yes; because they are parallel lines.
(b) Yes; because they are intersecting lines.
(c) No; because they are parallel lines.
(d) No; because they are intersecting lines.
Answer
B
Question. Naveen wants to plant some saplings in columns. If he increases the number of saplings in a column by 4, the number of columns decreases by 1. If he decreases the number of saplings by 5 in a column, the number of columns increased by 2. Which of these graphs relates the number, x, of columns and the number, y, of plants in a column?

Answer
C
Question. For which value(s) of p, will the lines represented by the following pair of linear equations be parallel?
3x −y − 5 = 0
6x − y 2−p = 0
(a) all real values except 10
(b) 10
(c) 5/2
(d) 1/2
Answer
A
Question. The value of k for which the lines (k + 1) x + 3ky + 15 = 0 and 5x + ky + 5 = 0 are coincident is
(a) 14
(b) 2
(c) –14
(d) –2
Answer
A
Question. Shipra gave a note of ™ 2,000 for a pair of jeans worth ™ 500. She was returned 11 notes in denominations of ™ 200 and ™ 100. Which pair of equations can be used to find the number of ™ 200 notes, x, and the number of ™ 100 notes y? How many notes of ™ 200 did she get?
(a) x+y = 11 and 200x+100y = 1500; 4
(b) x = y+11 and 200x+100y = 2000; 4
(c) x+y = 15 and 200x+100y = 1800; 10
(d) x+y = 15 and 100x+200y = 1800; 12
Answer
A
Question. The value of a for which the pair of equations 10x + 5y = a – 5, 20x + 10y – a = 0 has infinitely many solutions is
(a) 5
(b) –10
(c) 10
(d) 20
Answer
C
Question. In the equations shown below, a and b are unknown constants.
3ax + 4y = −2
2x + by = 14
If (–3, 4) is the solution of the given equations, what are the values of a and b?
(a) a = 5, b = 2
(b) a = 5, b = –2
(c) a = 2, b = 5
(d) a = –2, b = 5
Answer
C
Question. If x = a, y = b is the solution of the equations x – y = 2 and x + y = 4, then the values of a and b are, respectively
(a) 3 and 5
(b) 5 and 3
(c) 3 and 1
(d) –1 and –3
Answer
C
Question. Consider the graph shown.

Which of these is true about the given graph?
(a) These lines have infinitely many solutions as they lie in the same quadrant.
(b) These lines have a unique solution as they are intersecting at a point.
(c) These lines have a unique solution as the coefficient of x in both the equations is one.
(d) These lines have infinitely many solutions as they lie in the same quadrant.
Answer
B
Question. Which of these linear equations have a unique solution?

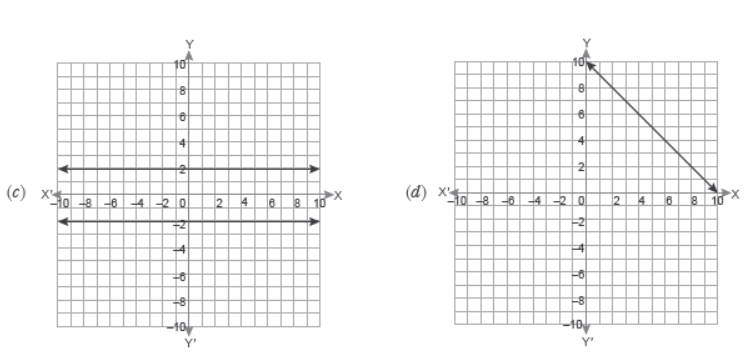
Answer
B
Question . The cost of production per unit for two products, A and B, are ™ 100 and ™ 80 respectively. In a week, the total production cost is ™ 32000. In the next week, the production cost reduces by 20%, and the total cost of producing the same number of units of each product is ™ 25600. Which of these are the equations that can be used to find the number of units of A, x, and the number of units of B, y?
(a) 100x + 80y = 32000 and 80x + 64y = 25600
(b) 100x + 64y = 32000 and 80x + 100y = 25600
(c) 80x + 64y = 25600 and 80x + 64y = 32000
(d) 80x + 80y = 32000 and 100x + 64y = 25600
Answer
B
Question. The pair of equations 5 x – 15y = 8 and 3x – 9 y = 24/5 has
(a) one solution
(b) two solutions
(c) infinite solutions
(d) no solution
Answer
C
Question. Raghav earned ™ 3550 by selling some bags each for ™ 500 and some baskets each for ™ 150. Aarav earned ™ 3400 by selling the same number of bags each for ™ 400 and the same number of baskets each for ™ 200 as Raghav sold. Which of these equations relates the number of bags x, and the number of baskets, y?
(a) 500x + 150y = 3400 and 400x + 200y = 3550
(b) 400x + 150y = 3550 and 500x + 200y = 3400
(c) 500x + 150y = 3550 and 400x + 200y = 3400
(d) 500x + 200y = 3550 and 400x + 150y = 3400
Answer
C
Question. If the lines given by 3x + 2ky = 8 and 2x + 5y – 4 = 0 are parallel, then the value of k is
(a) –5/4
(b) 15/4
(c) 2/5
(d) 3/2
Answer
B
Question. One of the common solution of ax + by = c and y-axis is
(a) (0, c/b)
(b) (0, b/c)
(c) (c/b, 0)
(d) (0, –c/b)
Answer
A
Question. Consider the equations shown.
4x + 3y = 41
x + 3y = 26
Which of these is the correct way of solving the given pair of equations?
(a) 4x + x + 3y − 3y = 41 − 26
(b) 4x + 3y + 3y = 41 − 26
(c) 4x − x + 3y − 3y = 41 − 26
(d) 4(x + 3y) + 3y = 41
Answer
C
Question. Every linear equation in two variables has ………….. solutions.
(a) no
(b) one
(c) two
(d) infinitely many
Answer
D
Question. If a pair of linear equations has infinitely many solutions, then the lines representing them will be
(a) parallel
(b) intersecting or coincident
(c) always intersecting
(d) always coincident
Answer
D
Question. The sum of two numbers is 1000 and the difference between their squares is 256000, then the numbers are
(a) 616 and 384
(b) 628 and 372
(c) 564 and 436
(d) None of them
Answer
B
Question. Graphically, the pair of equations 6x – 3y + 10 = 0; 2x – y + 9 = 0 represents two lines which are
(a) intersecting at exactly one point
(b) intersecting at exactly two points
(c) coincident
(d) parallel
Answer
D
Question. If a pair of linear equations is consistent, then the lines will be
(a) parallel
(b) always coincident
(c) intersecting or coincident
(d) always intersecting
Answer
C
Question. The sum of a two digit number and the number obtained by interchanging its digits is 99. If the digits differ by 3 then the number is
(a) 36
(b) 33
(c) 66
(d) None of them
Answer
A
Question. If x2n – 1 ym – 4 0 + = is a linear equation, which of these is also a linear equation?
(a) xn+ ym=0
(b) x 1/n+ y m/5=0
(c) xn +1/2+ ym+ 4 =4
(d) x m/5 + ym/5= 0
Answer
B
Question. The solution of the equations x+2y = 1.5 and 2x+ y = 1.5 is
(a) x = 1 and y = 1
(b) x = 1.5 and y = 1.5
(c) x = 0.5 and y = 0.5
(d) None of these
Answer
C
Question. Sum of two numbers is 35 and their difference is 13, then the numbers are
(a) 24 and 12
(b) 24 and 11
(c) 12 and 11
(d) None of these
Answer
B
Question. The value of k for which the system of equations x – 2y = 3 and 3x+ky = 1 has a unique solution is
(a) k = – 6
(b) k ≠ – 6
(c) k = 0
(d) no value
Answer
B
Question. The pair of linear equations 3x/2+ 5y/3 = 7 and 9x + 10y = 14 is
(a) consistent
(b) inconsistent
(c) consistent with one solution
(d) consistent with many solutions
Answer
B
Question. Which of the following is the other name for a pair of linear equations in two variables?
(a) Consistent equations
(b) Simultaneous equations
(c) Inconsistent equations
(d) Dependent equations
Answer
B
Question. What is the solution of the equations, 3x – y + 1/3 = 2x + y + 2/5 = 3x + 2y + 1/6 ?
(a) x = -1,y = -1
(b) x =1, y =1
(c) x =1, y = 2
(d) x = 2,y =1
Answer
B
Question. Two numbers differ by 3 and their product is 54. Find the numbers.
(a) 9 and 6
(b) -9 and -6
(c) Both (a) and (b)
(d) 9 and -4
Answer
C
Question. The smallest angle of a triangle is one-fifth the sum of the other two and the largest angle exceeds the sum of the other two by 20° . Find the largest angle of the triangle.
(a) 100°
(b) 90°
(c) 120°
(d) 110°
Answer
A
Question. The difference between two numbers is 5 and the difference between their squares is 65. Find the larger number.
(a) 9
(b) 10
(c) 11
(d) 12
Answer
A
Question. Find the solution of the equations 8x+ 9y = 6xy , 10x + 6y = 19xy .
(a) x = 3/2 , y = 3/2
(b) x = 2/3 , y = 3/2
(c) x = 3/2 , y = 2/3
(d) x = 3, y = 2
Answer
C
Question. How many solutions do the equations satisfying a1/a2 = b1/b2 = c1/c2 have?
(a) One
(b) Two
(c) Three
(d) Infinitely many
Answer
D
Question. What is a system of simultaneous equations called if it has no solution?
(a) Consistent system
(b) independent system
(c) Inconsistent system
(d) Dependent system
Answer
C
Question. Which of the following is a solution of 2p + 3q = 5 ?
(a) 2p + 3q = 5
(b) p = 1, q = 11
(c) p =1,q =1
(d) p = -1,q = -1
Answer
C
Question. Which of the following is the solution of the system of equations 4/x + 5y = 7 and 3/x + 4y = 5 ?
(a) x = -1/3 , y = -1
(b) x = 1/3 , y = -1
(c) x = -1/3 , y = 1
(d) x = 1/3 , y = 1
Answer
B
Question. The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes , 2 1 then the fraction is
(a) 4/4
(b) 5/7
(c) 6/7
(d) 8/7
Answer
B
Question. The coordinates of the vertices of triangle formed between the lines and y-axis from the graph is
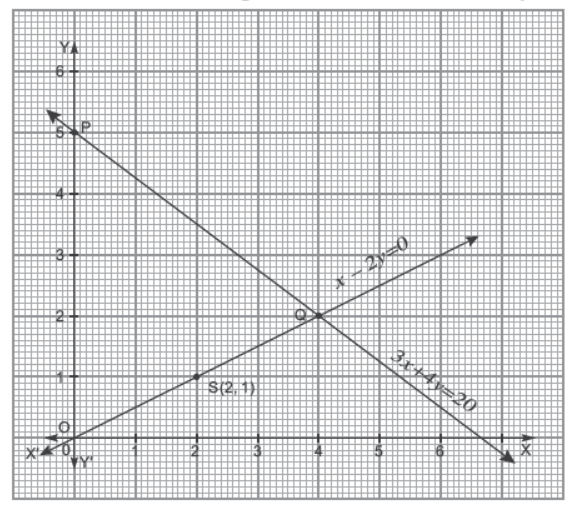
(a) (0, 5), (0, 0) and (6.5, 0)
(b) (4, 2), (6, 0) and (6.5, 0)
(c) (4, 2), (0, 0) and (0, 5)
(d) none of these
Answer
C
Question. The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son. The present ages (in years) of the son and the father are, respectively.
(a) 4 and 24
(b) 5 and 30
(c) 6 and 36
(d) 3 and 24
Answer
C
Question. Which of these is a linear equation in two variables?
(a) 3x – 2y + 2 = 0
(b) x + x2 – 2y + 8 = 0
(c) x – 2y + 10 = x2 + y
(d) 5x – 2y = 0
Answer
D
Question. The sum of the digits of a two-digit number is 9. If 27 is added to it, the digit of number get reversed. The number is
(a) 25
(b) 72
(c) 63
(d) 36
Answer
D
Question. When L1 and L2 are coincident, then the graphical solution of system of linear equation have
(a) infinite number of solutions
(b) unique solution
(c) no solution
(d) one solution
Answer
A
Question. Five years hence, fathers age will be three times the age of his daughter. Five years ago father was seven times as old as his daughter. Their present ages are
(a) 20 years, 10 years
(b) 40 years, 20 years
(c) 40 years, 10 years
(d) 30 years, 10 years
Answer
C
Fill in the Blanks :
Question. The number of common solutions for the system of linear equations 5x + 4y + 6 = 0 and 10x + 8y = 12 is ………….
Answer
zero
Question. Two distinct natural numbers are such that the sum of one number and twice the other number is 6. The two numbers are …………..
Answer
4 and 1
Question. If 2x + 3y = 5 and 3x + 2y = 10, then x – y = …………… .
Answer
5
Question. Sum of the ages of X and Y, 12 years, ago, was 48 years and sum of the ages of X and Y, 12 years hence will be 96 years. Present age of X is …………..
Answer
Cannot be determined
Question. If p + q = k, p – q = n and k > n, then q is ………………. .
Answer
positive

We hope you liked the above Linear Equations MCQ Class 10 Mathematics. In case you have any questions please put them in the comments box below and our teachers will provide you a response.


