Linear Inequalities MCQ Class 11 Mathematics
Please refer to Chapter 6 Linear Inequalities MCQ Class 11 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 11 Mathematics. Students should refer to MCQ Questions for Class 11 Mathematics with Answers to score more marks in Grade 11 Mathematics exams. Students should read the chapter Linear Inequalities and then attempt the following objective questions.
MCQ Questions Class 11 Mathematics Chapter 6 Linear Inequalities
The Linear Inequalities MCQ Class 11 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question: If the roots of the equation x2+2ax+ b= 0 are real and distinct and they differ by atmost 2m, then b lies in the interval
(a)(-a2-m2,a2)
(b)(a2-m2,a2)
(c)(a2,m2+a2)
(d) None of the above
Answer
B
Question: If one root of the equation x2+ px+ 12 =0 is 4, while the equation x2+px+q=0 has equal roots, then the value of q is
(a) 49/4
(b) 4/49
(c) 4
(d) None of these
Answer
A
Question:The number of values of the triplet (a, b, c) for which,acos2 x+ bsin2x+c=0 is satisfied by all real x, is
(a) 0
(b) 2
(c) 3
(d) infinite
Answer
D
Question: If tan A and tan B are the roots of the quadratic equation x2-px+q=0 then the value of sin2 (A+B) is

Answer
D
Question: If a and b are rational and b is not a perfect square, then the quadratic equation with rational coefficients whose one root is 1/
a+√b, is
(a) x2-2ax+(a2-b)=0
(b)(a2-b)x2-2ax+1=0
(c) (a2-b)x2-2bx+1=0
(d) None of the above
Answer
B
Question: The value of a, for which the equation x2– (sinα-2)x- (1+sinα)= 0 has roots, whose sum of square is
least, is
(a)π/4
(b) π/3
(c) π/2
(d) π/6
Answer
C
Question: If(2x2-3x+1)(2x2+5x+1)=9x2, then equation has
(a) four real roots
(b) two real and two imaginary roots
(c) four imaginary roots
(d) None of the above
Answer
A
Question:
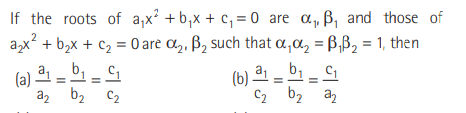
Answer
B
Question: If|x2|+|x |-2 =2 0, then the value of x is equal to
(a) 2
(b) – 2
(c) 1
(d) None of the above
Answer
C
Question: If X denotes the set of real number p for which the equation x2= p (x+p) has its roots greater than p, then X is equal to
(a)(-2,-1/2)
(b)(-1/2,1/4)
(c) Φ
(d) (-∞,0)
Answer
C
Question: If ax2+bx+6=0 does not have two distinct real roots, then the least value of 3a+ b is
(a) 2
(b) – 2
(c) 1
(d) – 1
Answer
B
Question: Conditions on a and b for which x2-ax-b2 is less than zero for atleast one positive x, are
(a) a>3,b<0
(b) a>3,b>0
(c) a, b ∈ R
(d) None of these
Answer
C
Question: The roots of ax2+bx+c=0,where a ≠ 0 and coefficients are real ,non-real complex and a+ c< b, then
(a) 4a+c>2b
(b) 4a+c<2b
(c) 4a+c=2b
(d) None of the above
Answer
B
Question: The value of a for which 2x2-2(2a+1) x+a (a+1)=0 may have one root less than a and other root greater than a, is
(a) – 1<a<0
(b) a > 0 or a < -1
(c) a ≥ 0
(d) -1/2<a<0
Answer
B
Question: Find all values of p, so that 6 lies between the roots of the equationx2+2(p-3)x+9=0
(a)(-∞,3/4)
(b)(-∞,3/4)
(c) (3/4∞)
(d) None of thes
Answer
B
Question:
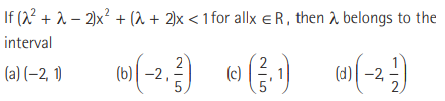
Answer
B
Question:
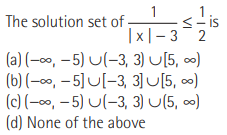
Answer
A
Question:
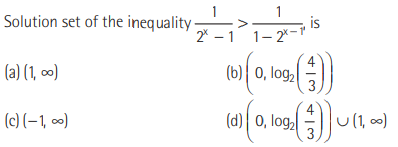
Answer
D
Question: If c< d, x2+(c+d) x +cd <0, then x
(a) (-d,-c)
(b) (-d,-c)
(c) R
(d) S
Answer
B
Question:
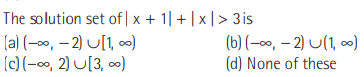
Answer
B
Question:
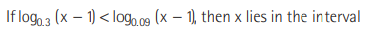
(a) (2,∞)
(b) (1, 2)
(c) (-2,-1)
(d) None of these
Answer
A
Question:
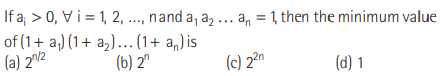
Answer
B
Question: If x2+x+ |x|+1≤ 0, then x lies in
(a) (0,∞)
(b) (-∞,0)
(c) R
(d) Φ
Answer
D
Question:
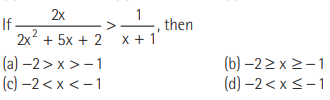
Answer
C
Question: If (ax2+c) y+(a’x2+c’)=0 and x is a rational function of y and ac is negative, then
(a) ac’ +a’c=0
(b) a/a’=c/c’
(c) a2+c2=a‘2+c‘2
(d) aa’+cc’=1
Answer
B
Question: If the roots of the equation (p2+q2)x2-2q(p+r)x+(q2+r2)=0 be in real and equal, then p q r , and will be in
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
B
Question: If roots of the equation (a-b)x2+(c-a)x+(b-c)=0 ) are equal, then a,b and c are in
(a) AP
(b) HP
(c) GP
(d) None of these
Answer
A
Question: If a >0, b>0,c>0, then both the roots of the equation ax2+ bx+c = 0
(a) are real and negative
(b) have negative real part
(c) are rational numbers
(d) None of these
Answer
B
Question:
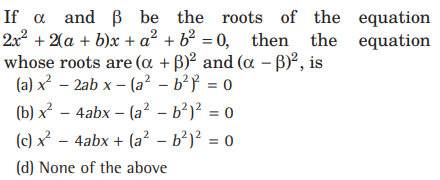
Answer
B
Question: If roots of the equation ax2+bx+c=0;(a,b,c ∈ N) are rational numbers, then which of the following cannot be true ?
(a) All a, b and are c even
(b) All a b, and c are odd
(c) b is even while a and c are odd
(d) None of the above
Answer
D
Question:
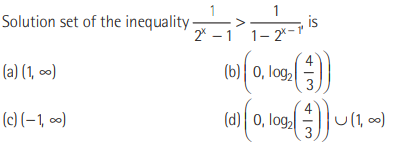
Answer
D
Question: Let α,β be the roots of x2-2x cos Φ+1then the equation whose roots are an and βn , is
(a) x2-2x cos nΦ-1=0
(b) x2-2x cos nΦ +1=0
(c) x2-2x sin nΦ+1=0
(d) x2+2x sin nΦ-1=0
Answer
B
Question: If α and β are the roots of the equation ax2+bx+c=0, then the equation whose roots are a+1/β and β+1/α,, is
(a) ac x2+(a+c) bx+(a+c)2=0
(b) abx2+ (a+ c) bx+(a+c)2=0
(c) ac x2+ (a+ b) cx +(a+c)2=0
(d) None of the above
Answer
A
Question: Let α and α2be the roots of x2+x+1=0, then the equation whose roots are α31 and α 62 , is
(a) x2-x+1=0
(b) x2+x-1=0
(c) x2+x+1=0
(d) x 60+x30+1=0
Answer
C
Question: If at least one root of the equation x3+ax2+bx+c=0 ax remains unchanged, when a b, and c are decreased by one, then which one of the following is always a root of the given equation ?
(a) 1
(b) -1
(c) w, an imaginary cube root of unity
(d) i
Answer
C
Question: If the equation 2x2+3x+5λ=0 and x2+2x+3λ=0 have a common root, then λ is equal to
(a) 0
(b) -1
(c) 0, -1
(d) 2, -1,
Answer
C
Question: If each pair of the equation
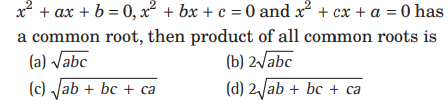
Answer
A
Question: If at least one root of 2x2+3x+5=0 and ax2+bx+c=0,a,b,c ∈ N is common, then the maximum value of a+ b+ c is
(a) 10
(b) 0
(c) does not exist
(d) None of these
Answer
C
We hope you liked the above Linear Inequalities MCQ Class 11 Mathematics. In case you have any questions please put them in the comments box below and our teachers will provide you a response
