Matrices MCQ Questions Class 12 Mathematics
Please refer to MCQ Questions for Class 12 Mathematics Chapter 3 Matrices with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 12 Mathematics. Students should refer to MCQ Questions for Class 12 Mathematics with Answers to score more marks in Grade 12 Mathematics exams. Students should read the chapter Matrices and then attempt the following objective questions.
MCQ Questions for Class 12 Mathematics Chapter 3 Matrices with answers
MCQ Questions for Class 12 Mathematics Chapter 3 provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. The order of the single matrix obtained from
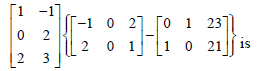
(a) 2 × 3
(b) 2 × 2
(c) 3 × 2
(d) 3 × 3
Answer
D
Question.
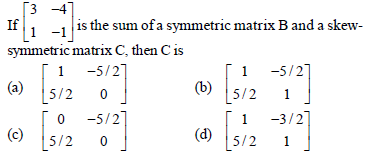
Answer
C
Question.
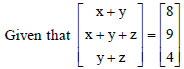
then x =
(a) 2
(b) 3
(c) 4
(d) 5
Answer
D
Question. If A is a square matrix, then AA’ is a
(a) skew-symmetric matrix
(b) symmetric matrix
(c) diagonal matrix
(d) None of these
Answer
B
Question. For any two matrices A and B, we have
(a) AB = BA
(b) AB ≠ BA
(c) AB = O
(d) None of these
Answer
D
Question. What is true about matrix multiplication ?
(a) It is commutative.
(b) It is associative.
(c) Both of the above.
(d) None of the above.
Answer
B
Question. If A = [aij] is a matrix of order 4 × 5, then the diagonal elements of A are
(a) a11, a22, a33, a44
(b) a55, a44, a33, a22, a11
(c) a11, a22, a33
(d) do not exist
Answer
D
Question. If A is symmetric as well as skew-symmetric matrix, then A is
(a) Diagonal
(b) Null
(c) Triangular
(d) None of these
Answer
B
Question. The number of all possible matrices of order 3 × 3 with each entry 0 or 1 is
(a) 18
(b) 512
(c) 81
(d) None of these
Answer
B
Question.
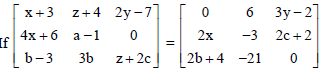
then, the values of a, b, c, x, y and z respectively are
(a) – 2, – 7, – 1, – 3, – 5, – 2
(b) 2, 7, 1, 3, 5, – 2
(c) 1, 3, 4, 2, 8, 9
(d) – 1, 3, –2, –7, 4, 5
Answer
A
Question.
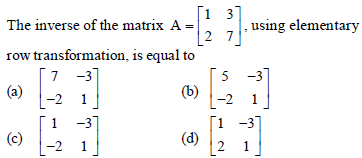
Answer
A
Question. Choose the incorrect statement.
(a) A matrix A = [3] is a scalar matrix of order 1
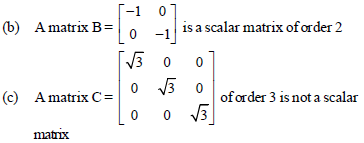
(d) None of the above
Answer
C
Question. The matrix X such that
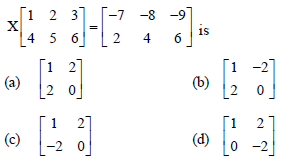
Answer
B
Question.
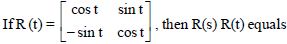
(a) R (s + t)
(b) R (s – t)
(c) R(s) + R(t)
(d) None of these
Answer
A
Question.
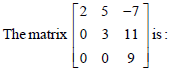
(a) symmetric
(b) diagonal
(c) upper triangular
(d) skew symmetric
Answer
C
Question. If A is any square matrix, then which of the following is skew-symmetric?
(a) A + AT
(b) A – AT
(c) AAT
(d) ATA
Answer
B
Question.
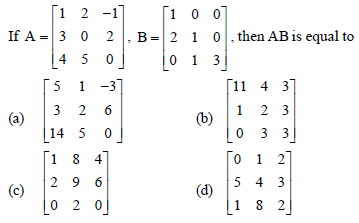
Answer
A
Question.
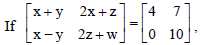
then the values of x, y, z and w respectively are
(a) 2, 2, 3, 4
(b) 2, 3, 1, 2
(c) 3, 3, 0, 1
(d) None of these
Answer
A
Question.
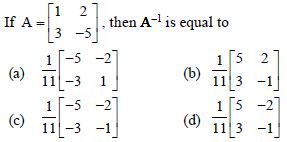
Answer
B
Question.
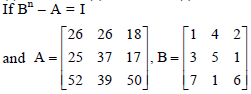
then n =
(a) 2
(b) 3
(c) 4
(d) 5
Answer
A
Question. If A is a m ×n matrix with entries aij, then the matrix A can be represented as
(a) A = [aij]m × n
(b) A = [aji]m × n
(c) A = [aij]n × m
(d) A = [aji]n × m
Answer
A
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
A B C
(a) 2 1 3
(b) 3 2 1
(c) 3 1 2
(d) 1 3 2
Answer
C
Question. If A = [aij]m × n, then A’ is equal to
(a) [aji]n × m
(b) [aij]m × n
(c) [aji]m × n
(d) [aij]n × m
Answer
A
Question. Using elementary transformation, the inverse of the matrix
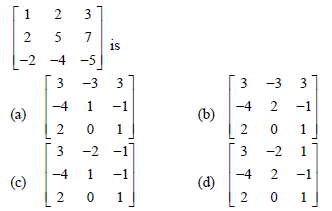
Answer
C
Question. If A, B are two square matrices such that AB = A and BA = B, then
(a) only B is idempotent
(b) A, B are idempotent
(c) only A is idempotent
(d) None of these
Answer
B
Question.
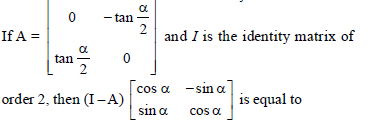
(a) I + A
(b) I – A
(c) A – I
(d) A
Answer
A
Question. Let A and B be two matrices then (AB)’ equals:
(a) B’A’
(b) A’B
(c) – AB
(d) 1
Answer
A
Question.
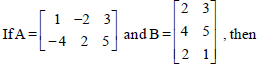
(a) AB, BA exist and are equal
(b) AB, BA exist and are not equal
(c) AB exists and BA does not exist
(d) AB does not exist and BA exists
Answer
B
Question. If A is a matrix having m rows and n columns, then the matrix A is called a matrix of order
(a) m × n
(b) n × m
(c) mn
(d) nm
Answer
A
Question. Let A = [aji] be an m × n matrix and B = [bjk] be an n × p matrix. Then, the product of the matrices A and B is the matrix C of order.
(a) n × m
(b) m × n
(c) p × m
(d) m × p
Answer
D
Question. If A is a square matrix of order m, then the matrix B of same order is called the inverse of the matrix A, if
(a) AB = A
(b) BA = A
(c) AB = BA = I
(d) AB = –BA
Answer
C
Question.
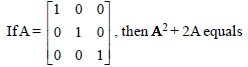
(a) 4A
(b) 3A
(c) 2A
(d) A
Answer
B
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.
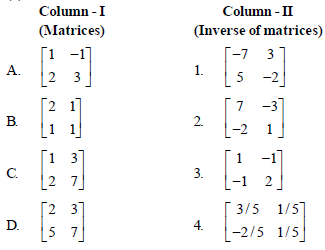
Codes
A B C D
(a) 2 3 1 4
(b) 4 3 2 1
(c) 3 4 1 2
(d) 3 1 4 2
Answer
B
Question. For any square matrix A, AAT is a
(a) unit matrix
(b) symmetric matrix
(c) skew-symmetric matrix
(d) diagonal matrix
Answer
B
Question.
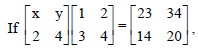
then y =
(a) 6
(b) 1
(c) 8
(d) 9
Answer
A
Question. The matrix C = [cik]m × p is the product of A = [aij]m × n and B = [bjk]n × p where cik is
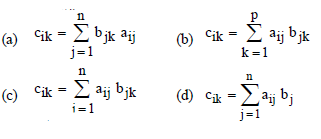
Answer
C
Question. If A is a square matrix such that A2 = I, then (A – I)3 + (A + I)3 – 7A is equal to
(a) A
(b) I – A
(c) I + A
(d) 3A
Answer
A
Question. If the diagonal elements of a diagonal matrix are all equal, then the matrix is called
(a) row matrix
(b) scalar matrix
(c) rectangular matrix
(d) None of the above
Answer
B
Question. If ω is a complex cube root of unity, then the matrix
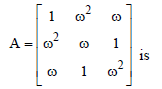
(a) symmetric matrix
(b) diagonal matrix
(c) skew-symmetric matrix
(d) None of these
Answer
A
Question.
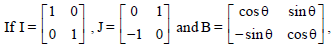
then value of B in terms of I and J is
(a) Isin θ + J cosθ
(b) Isin θ – J cosθ
(c) Icos θ + J sin θ
(d) –Isin θ + J cos θ
Answer
C
Question.
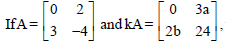
then the values of k, a, b are respectively.
(a) –6, –12, –18
(b) –6, 4, 9
(c) –6, –4, –9
(d) –6, 12, 18
Answer
C
Question.
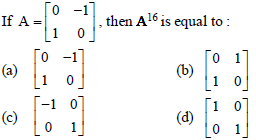
Answer
D
Question. A square matrix A = [aij]n×n is called a lower triangular matrix if aij = 0 for
(a) i = j
(b) i < j
(c) i > j
(d) None of these
Answer
B
STATEMENT TYPE QUESTIONS
Question. Consider the following statements
I. For multiplication of two matrices A and B, the number of columns in A should be less than the number of rows in B.
II. For getting the elements of the product matrix, we take rows of A and column of B, multiply them elementwise and take the sum.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Neither I nor II is true
Answer
B
Question. Consider the following statements
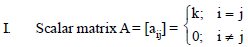
where k is a scalar, in an identity matrix when k = 1.
II. Every identity matrix is not a scalar matrix.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Both I and II are false
Answer
A
Question.
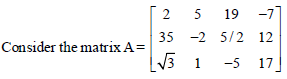
Now, consider the following statements
I. The order of the matrix is 4 × 3 and number of elements is 12.
II. The elements a13, a21, a33 are respectively19, 35, –5.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Neither I nor II is true
Answer
B
Question. Let A, B and C are three matrices of same order. Now, consider the following statements
I. If A = B, then AC = BC
II. If AC = BC, then A = B
Choose the correct option
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Neither I nor II is true
Answer
A
Question. Consider the following statements.
I. If a matrix has 24 elements, then all the possible orders it can have are 24 × 1, 1 × 24, 2 × 4, 4 × 2, 2 × 12, 12 × 2, 3 × 8, 8 ×3, 4 ×6 and 6 × 4.
II. For a matrix having 13 elements, its all possible orders are 1 × 13 and 13 × 1.
III. For a matrix having 18 elements, its all possible orders are 18 × 1, 1 × 18, 2 × 9, 9 × 2, 3 × 6, 6 × 3.
IV. For a matrix having 5 elements, its all possible orders are 1 × 5 and 5 × 1.
Choose the correct option
(a) Only I is false
(b) Only II is a false
(c) Only III is false
(d) All are true
Answer
A
Question. Consider the following statements
I. If AB and BA are both defined, then they must be equal i.e., AB = BA.
II. If AB and BA are both defined, it is not necessary that AB = BA.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) both I and II are true
(d) None of these
Answer
B
Question.
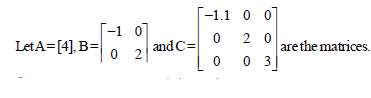
Consider the following statements
I. The matrices A, B and C are diagonal matrices.
II. The matrices A, B and C are of order 1, 3 and 2, respectively.
Choose the correct option.
(a) I is true and II is false
(b) I is false and II is true
(c) Both I and II are true
(d) Both I and II are false
Answer
A
