Probability MCQ Class 10 Mathematics
Please refer to Chapter 14 Probability MCQ Class 10 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 10 Mathematics. Students should refer to MCQ Questions for Class 10 Mathematics with Answers to score more marks in Grade 10 Mathematics exams. Students should read the chapter Probability and then attempt the following objective questions.
MCQ Questions Class 10 Mathematics Chapter 14 Probability
The Probability MCQ Class 10 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. The probability that a non-leap year selected at random will contain 53 sunday’s is
(a) 1/7
(b) 2/7
(c) 3/7
(d) 5/7
Answer
A
Question. To win a prize in a game, you need to first choose one of the 4 doors, 1, 2, 3, 4 and then need to choose one of the three boxes A, B, C and then need to choose between two colours red and green. How many of the possible outcomes of this game include selecting Box A and red colour?
(a) 2
(b) 4
(c) 8
(d) 12
Answer
B
Question. Which of the following can be probability of an event?
(a) 2
(b) –1
(c) 0.3
(d) 1.12
Answer
C
Question. If a number x is chosen from the numbers 1, 2, 3 and a number y is selected from the numbers 1, 4, 9. Then P(xy < 9) is
(a) 3/9
(b) 4/9
(c) 1/9
(d) 5/9
Answer
D
Question. When four coins are tossed simultaneously, which of the following represents the sample space?
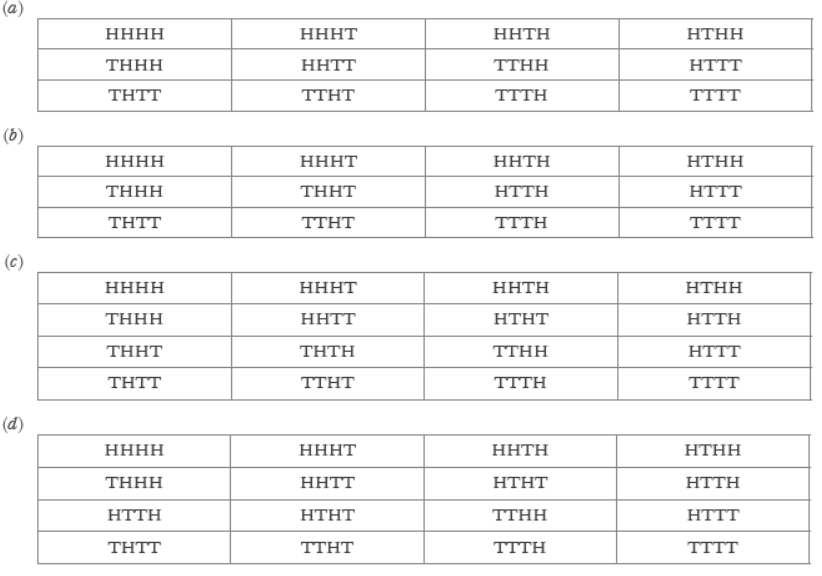
Answer
C
Question. A card is drawn from a deck of 52 cards. The event E is that card is not an ace of hearts. The number of outcomes favourable to E is
(a) 4
(b) 13
(c) 48
(d) 51
Answer
D
Question. A card is selected from a deck of 52 cards. The probability of being a red face card is
(a) 3/26
(b) 3/13
(c) 2/13
(d) 1/2
Answer
A
Question. Which of the following cannot be the probability of an event?
(a) 1/3
(b) 0.1
(c) 3%
(d) 17/16
Answer
D
Question. A die is thrown once. The probability of getting an even number is
(a) 1/3
(b) 1/6
(c) 1/4
(d) 1/2
Answer
D
Question. A girl calculates that the probability of her winning the first prize in a lottery is 0.08. If 6,000 tickets are sold, how many tickets has she bought?
(a) 40
(b) 240
(c) 480
(d) 750
Answer
C
Question. A card is selected at random from a well shuffled deck of 52 playing cards. The probability of its being a face card is
(a) 3/13
(b) 4/13
(c) 6/13
(d) 9/13
Answer
A
Question. Kirti has a box containing four cards labelled A, B, C and D. She randomly picks a card from the box, records the label on the card and put it back in the box. She repeats this experiment 80 times and records her observation in the table shown below.

Which of the following shows the empirical probability and theoretical probability of picking Card C the next time?
(a) Empirical probability = 5/11
(b) Empirical probability = 5 /11 Theoretical probability = 1/2 Theoretical probability = 1/4
(c) Empirical probability = 5/16
(d) Empirical probability = 5/16 Theoretical probability = 1/2 Theoretical probability = 1/4
Answer
D
Question. An event is very unlikely to happen. Its probability is closest to
(a) 0.0001
(b) 0.001
(c) 0.01
(d) 0.1
Answer
A
Question. Smita has a bag containing 1 red, 1 green, 1 yellow, 1 black and 1 blue ball. She randomly picks the ball from the bag notes it colour and keeps it back in the bag. She repeats this 40 times. The table shows the number of times each colour ball she gets. The number of times the black ball is picked is missing in the table.

She then repeats the experiment 10 more times and gets red ball twice, green ball once, yellow ball thrice, black ball once and blue ball thrice. Which of these is a valid conclusion as the number of trials of the experiment increases?
(a) The empirical probability of picking red ball becomes equal to its theoretical probability.
(b) The empirical probability of picking red ball does not get closer to its theoretical probability.
(c) The empirical probability of picking yellow ball gets closer to its theoretical probability.
(d) The empirical probability of picking yellow ball gets further away from its theoretical probability.
Answer
C
Question. If a card is drawn from a deck of cards, what is the probability of a card drawn to be a red or a black card and what can we say about that event?
(a) 0 and it is a sure event.
(b) 1 and it is a sure event.
(c) 0 and it is an impossible event.
(d) 1 and it is an impossible event.
Answer
B
Question. If a letter of English alphabet is chosen at random, than the probability that the letter is a consonant is
(a) 21/23
(b) 10/13
(c) 21/26
(d) 5/26
Answer
C
Question. A spinner is shown below.
Some of the events are listed below, when the spinner is spinned.
Event A: The spinner lands on a multiple of 11.
Event B: The spinner lands on a number less than 11.
Event C: The spinner lands on a number more than 10.
Which of the following statement is true about the three events?
(a) Probability of Event A is 1, so A is a sure event while the probabilities of Events B and C are 0, so they are impossible events.
(b) Probability of Event B is 1, so B is a sure event while the probabilities of Events A and C are 0, so they are impossible events.
(c) Probability of Event A is 1, so A is an impossible event while the probabilities of Events B and C are 0, so they are sure events.
(d) Probability of Event B is 1, so B is an impossible event while the probabilities of Events A and C are 0, so they are sure events.
Answer
B
Question. A card is drawn from a deck of 52 cards. The event E is that card is not an ace of hearts. The number of outcomes favourable to E is
(a) 4
(b) 13
(c) 48
(d) 51
Answer
D
Question. One card is drawn from a well shuffled deck of 52 cards. The probability that it is black queen is
(a) 1/26
(b) 1/13
(c) 1/52
(d) 2/13
Answer
A
Question. A box has 10 equal size cards. Of the 10 cards, 4 are blue, 3 are green, 2 are yellow and 1 is red. If a card is randomly drawn from the box, which is the colour that the card is most likely to have?
(a) Red
(b) Green
(c) Blue
(d) Yellow
Answer
C
Question. If an event cannot occur, then its probability is
(a) 1
(b) 3/4
(c) 1/2
(d) 0
Answer
D
Question. Of 50 students in a class, 16 prefer cricket, 8 prefer football, 8 prefer basketball and rest of the students prefer either tennis or hockey. There are twice as many students who prefer tennis as the number of students who prefer hockey. A student is randomly selected from the class.
Which statement is correct?
(a) The probability of selecting a student who prefer hockey is more than that of selecting a student who prefer football.
(b) The probability of selecting a student who prefer tennis is more than that of selecting a student who prefer football.
(c) The probability of selecting a student who prefer hockey is more than that of selecting a student who prefer tennis.
(d) The probability of selecting a student who prefer basketball is more than that of selecting a student who prefer cricket.
Answer
B
Question. A bag contains three green marbles, four blue marbles and two orange marbles. If a marble is picked at random, then the probability that it is not an orange marble is
(a) 7/9
(b) 2/9
(c) 4/9
(d) none of these
Answer
A
Question. If P(A) denotes the probability of an event A, then
(a) P(A) < 0
(b) P(A) > 1
(c) 0 ≤ P(A) ≤ 1
(d) –1 ≤ P(A) ≤ 1
Answer
C
Question. In a lottery, there are 8 prizes and 16 blanks. The probability of getting a prize is
(a) 2/3
(b) 1/3
(c) 1/2
(d) 1/4
Answer
B
Question. A bag contains 3 red, 5 black and 7 white balls. A ball is drawn from the bag at random. The probability that the ball drawn is not black, is
(a) 1/3
(b) 9/15
(c) 5/10
(d) 2/3
Answer
D
Question. Which of the following can be the probability of an event?
(a) 0.04
(b) 1.004
(c) 18/23
(d) 8/7
Answer
C
Question. The probability that a number selected at random from the numbers 1, 2, 3 … 15 is a multiple of 4 is
(a) 4/15
(b) 2/15
(c) 1/5
(d) 1/3
Answer
C
Question. A bag contains 3 red balls, 5 white balls and 7 black balls. What is the probability that a ball drawn from the bag at random will be neither red nor black?
(a) 1/5
(b) 1/3
(c) 7/15
(d) 8/15
Answer
B
Question. The probability of throwing a number greater than 2 with a fair die is
(a) 1/3
(b) 2/3
(c) 1/4
(d) 3/5
Answer
B
Question. When a die is thrown, the probability of getting an even number less than 4 is
(a) 1/4
(b) 0
(c) 1/2
(d) 1/6
Answer
D
Question. If the probability of an event is p, the probability of its complementary event will be
(a) p – 1
(b) 1 – p
(c) 1-1/P
(d) p
Answer
B
Question. A card is selected at random from a well shuffled deck of 52 playing cards. The probability of its being a face card is
(a) 3/13
(b) 4/13
(c) 6/13
(d) 9/13
Answer
A
Question. The probability of getting a number from 1 to 100, which is divisible by 7 is
(a) 1/7
(b) 14/100
(c) 7/100
(d) 23/98
Answer
B
Question. The probability of getting exactly one head in tossing a pair of coins is
(a) 0
(b) 1
(c) 1/3
(d) 1/2
Answer
D
Question. If a pair of dice is thrown, the probability of getting a sum of 10 is
(a) 1/12
(b) 1/36
(c) 1/9
(d) 1/4
Answer
A
Question. If a pair of dice is thrown, then the probability of getting a doublet is
(a) 1/3
(b) 1/6
(c) 5/12
(d) 2/3
Answer
B
Question. If a bag contains 3 red and 7 black balls, the probability of getting a black ball is
(a) 3/10
(b) 4/10
(c) 7/10
(d) 5/10
Answer
C
Question. Which of the following cannot be the probability of an event?
(a) 1/3
(b) 0.1
(c) 3%
(d) 17/6
Answer
D
Question. Two coins are tossed simultaneously. The probability of getting atmost one head is
(a) 1/4
(b) 1/2
(c) 3/4
(d) 1
Answer
C
Question. A coin is tossed 1000 times and 640 times a ‘head’ occurs. The empirical probability of occurrence of a head in this case is
(a) 0.6
(b) 0.64
(c) 0.36
(d) 0.064
Answer
B
Question. If an event cannot occur, then its probability is
(a) 1
(b) 3 4
(c) 1 2
(d) 0
Answer
D
Question. The distance between the points (cos θ, −sin θ) and (−cos θ, sin θ) is 1
(a) 3
(b) 4
(c) 2
(d) 5
Answer
C
Question. The probability expressed as a percentage of a particular occurrence can never be
(a) less than 100
(b) less than 0
(c) greater than 1
(d) anything but a whole number
Answer
B
Question. The lengths of the diagonals of a rhombus are 16 cm and 12 cm. Then the length of the side of the rhombus is
(a) 9 cm
(b) 10 cm
(c) 8 cm
(d) 20 cm
Answer
B
Question. The value of sin 60° cos 30° + sin 30° cos 60° is
(a) 0
(b) 1
(c) 2
(d) 5
Answer
B
Question. The (HCF × LCM) for the numbers 50 and 20 is 1
(a) 10
(b) 100
(c) 1000
(d) 50
Answer
C
Question. The diameter of circle whose area is equal to sum of area of two circles of diameter 16 cm and 12 cm is
(a) 56 cm
(b) 42 cm
(c) 28 cm
(d) 20 cm
Answer
D
Question. The value of sin 45° + cos 45° is 1
(a) 1/√ 2
(b) √2
(c) 2
(d) 2√ 2
Answer
B
Question. The zeroes of the quadratic polynomial x2 + 13x + 40 are 1
(a) –10, –4
(b) 8, 5
(c) – 8, – 5
(d) 20, 2
Answer
C

We hope you liked the above Probability MCQ Class 10 Mathematics. In case you have any questions please put them in the comments box below and our teachers will provide you a response.


