Please refer to Chapter 12 Surface Area and Volume MCQ Class 10 Mathematics with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 10 Mathematics. Students should refer to MCQ Questions for Class 10 Mathematics with Answers to score more marks in Grade 10 Mathematics exams. Students should read the chapter Surface Area and Volume and then attempt the following objective questions.

MCQ Questions Class 10 Mathematics Chapter 12 Surface Area and Volume

The Surface Area and Volume MCQ Class 10 Mathematics provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.

Question. The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cmis:
(a) 4.2
(b) 2.1
(c) 8.1
(d) 1.05

Question. If the curved surface area of a solid right circular cylinder of height h and radius r is one-third ofits total surface area, then
(a) h = r
(b) h = r
(c) h = r
(d) h = 2r

Question. A surahi is the combination of:
(a) a sphere and a cylinder
(b) a hemisphere and a cylinder
(c) two hemispheres
(d) a cylinder and a cone

Question. A right circular cylinder of radius r cm and height h cm (h > 2r) just encloses a sphere of diameter
(a) r cm
(b) 2r cm
(c) h cm
(d) 2h cm

Question. If the volume of a cube is 343 cm , then its edge is
(a) 9cm
(b) 8cm
(c) 49cm
(d) 7cm

Question. The volume of the cuboid whose length, breadth and height is 12cm, 8cm and 6cm is
(a) 568 cu.cm
(b) 576 cu.cm
(c) 576 sq.cm
(d) 570 cu.cm

Question. A shuttlecock used for playing badminton has the shape of the combination of
(a) a cylinder and a sphere
(b) a sphere and a cone
(c) a cylinder and a hemisphere
(d) frustum of a cone and a hemisphere

Question. If the diameter of a metallic sphere is 6 cm, it is melted and a wire of diameter 0·2 cm is drawn,then the length of the wire made shall be
(a) 24 m
(b) 28 m
(c) 32 m
(d) 36 m

Question. The cost of painting a cubical box of side 3m at the rate of Rs.2 per sq.m is
(a) Rs.108
(b) Rs.120
(c) Rs.125
(d) Rs.112

Question. The radius and height of a right circular cone and that of a right circular cylinder are respectivelyequal. If the volume of the cylinder is 300 cu.cm, then the volume of the cone is
(a) 300 cu.cm
(b) 100 cu.cm
(c) 600 cu.cm
(d) 900 cu.cm

Question. A conical tent with base-radius 7 m and height 24 m is made from 5 m wide canvas. The length ofthe canvas used is (Take π = )
(a) 100 m
(b) 105 m
(c) 110 m
(d) 115 m

Question. A cube whose edge is 20 cm long, has circles on each of its faces painted black. What is the totalarea of the unpainted surface of the cube if the circles are of the largest possible areas?
(a) 90.72 cm²
(b) 256.72 cm²
(c) 330.3 cm²
(d) 514.28 cm²

Question. The volumes of two spheres are in the ratio 125 : 64. The ratio of their surface areas is
(a) 9 : 16
(b) 16 : 9
(c) 25 : 16
(d) 16 : 25

Question. A container (open at the top) made up of metal sheet is in the form of a frustum of a cone ofheight 16 cm with radii of its lower and upper ends 8cm and 20 cm respectively. The amount ofliquid the container can hold is (Take π = 3.14)
(a) 104.49 |
(b) 10.95 |
(c) 12 |
(d) 10.45 |

Question. The total surface area of a hemispherical solid having radius 7 cm is
(a) 462 cm²
(b) 294 cm²
(c) 588 cm²
(d) 154 cm²

Question. A mason constructs a wall of dimensions 270 cm × 300 cm × 350 cm with the bricks each of size22.5 cm × 11.25 cm × 8.75 cm and it is assumed that 1/8 space is covered by the mortar. Then the number of bricks used to construct the wall is
(a) 11100 cm
(b) 11200 cm
(c) 11000 cm
(d) 11300 cm

Question. If two solid hemispheres of same base radius are joined together along their bases, then curvedsurface area of this new solid is
(a) 3πr ²
(b) 4πr ²
(c) 5πr ²
(d) 6πr ²

Question. If the radius and height of a cylinder are in the ratio 5 : 7 and its volume is 550 cm 3 , then its radiusis equal to (Take π = )
(a) 5 cm
(b) 7 cm
(c) 6 cm
(d) 10 cm

Question. If a solid metallic sphere of radius 8 cm is melted and recasted into n spherical solid balls ofradius 1 cm, then n =
(a) 500
(b) 510
(c) 512
(d) 516

Question. The curved surface area of glass having radii 3 cm and 4 cm respectively and slant height 10 cm is
(a) 55 cm²
(b) 110 cm²
(c) 220 cm²
(d) 440 cm²

Question. A piece of paper is in the shape of a semi¬circular region of radius 10 cm. It is rolled to form aright circular cone. The slant height is
(a) 5 cm
(b) 10 cm
(c) 15 cm
(d) 20 cm

Question. A solid piece of iron in the form of a cuboid of dimensions 49 cm × 33 cm × 24 cm, is moulded to form a solid sphere. The radius of the sphere is
(a) 21 cm
(b) 23 cm
(c) 25 cm
(d) 19 cm

Question. The base area of the cylinder is 80 sq.cm. If its height is 5cm, then its volume is
(a) 200 cu.cm
(b) 80 cu.cm
(c) 100 cu.cm
(d) 400 cu.cm

Question. The radii of the top and bottom of a bucket of slant height 13 cm are 9 cm and 4 cm respectively.The height of the bucket is
(a) 10 cm
(b) 12 cm
(c) 15 cm
(d) 16 cm

Question. The internal and external diameter of a hollow hemispherical vessel are 42 cm and 45.5 cm. respectively. Find its capacity (volume) and also its outer curved surface area.
(a) 5.27 litres, 3253.25 cm²
(b) 5.20 litres, 3253.25 cm²
(c) 5.27 litres, 3200.18 cm²
(d) 5.27 litres, 3250.25 cm²

Question. Three identical cones with base radius r are placed on their bases so that each is touching the other two. The radius of the circle drawn through their vertices is –     
(a) smaller than r
(b) equal to r
(c) larger than r
(d) depends on the height of the cones

Question. The diameter of hollow cone is equal to the diameter of a spherical ball. If the ball is placed at the base of the cone, what portion of the ball will be outside the cone?   
(a) 50%
(b) less than 50%
(c) more than 50%
(d) 100% 

Question. The diagram shows the parts of a right cylinder. The volume of the cylinder, in cm³ is     

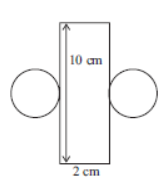
(a) 20/ π   
(b) 50/ π
(c) 25 /π
(d) 40 π

Question. Cubes A, B, C having edges of 18 cm, 24 cm and 30 cm respectively are melted and moulded into a new cube D. Find the edge of the bigger cube D.       
(a) 32
(b) 28
(c) 39
(d) 36

Question. If h, c, v are respectively the height, the C.S.A and the volume of a cone, find the value of 3πvh³ – c²h² + 9v²   
(a) 1
(b) 2
(c) 0
(d) 3

Question. The height of a conical tent is 14 m and its floor area is 346.5 m². The length of canvas, 11m wide, required for it is.   
(a) 490 m
(b) 525 m
(c) 665 m
(d) 860 m

Question. If the perimeter of one face of a cube is 20 cm, then its surface area is     
(a) 120 cm² 
(b) 150 cm²
(c) 125 cm²
(d) 400 cm²

Question. A cube of side 12 cm is painted red on all the faces and then cut into smaller cubes, each of side 3 cm. What is the total number of smaller cubes having none of their faces painted?     
(a) 16
(b) 8
(c) 12
(d) 24

Question. If the diameter of the sphere is doubled, the surface area of the resultant sphere becomes x times that of the original one, then x would be     
(a) 2
(b) 3
(c) 4
(d) 8

Question. Volumes of two spheres are in the ratio 125 : 64. The ratio of their surface areas will be     
(a) 5 : 4
(b) 25 : 16
(c) 16 : 25
(d) 125 : 64

Question. If the radius of the sphere is increased by 100%, the volume of the corresponding sphere is increased by   
(a) 200%
(b) 500%
(c) 700%
(d) 800%

Question. Given three cubes with integer side lengths, if the sum of surface areas of three cubes is 498 sq. cm, then the sum of the volumes of the cubes in all possible solutions is     
(a) 731
(b) 495
(c) 1226
(d) None of these

Question. A slab of ice 8 inches in length, 11 inches in breadth, and 2 inches thick was melted and resolidified in the form of a rod of 8 inches diameter. The length of such a rod, in inches, is  nearest to       
(a) 3 
(b) 3.5
(c) 4
(d) 4.5

Question. If a solid of one shape is converted to another, then the volume of the new solid
(a) remains same
(b) increases
(c) decreases
(d) can’t say

Question. Which one of the following is/are incorrect ?     
(a) Total surface area of cuboid is 2(lb + bh + hl)
(b) Total surface area of a cube is 4l²
(c) Area of four walls = 2h (l + b)
(d) Area of four walls = Height × Perimeter of the room

Question. The volume of a cylinder is 448 p cm³ and height 7 cm. Find its lateral surface area and total surface area is     
(a) 253 cm²
(b) 352 cm²
(c) 532 cm²
(d) 325 cm²

Question. The diameter of a garden roller is 1.4 m, and 2m long. How much area will it cover in 5 revolutions.     
(a) 44 m²
(b) 140 m²
(c) 440 m²
(d) 220 m²

Question. The base radii of a cone and a cylinder are equal. If their curved surface areas are also equal, then the ratio of the slant height of the cone to the height of the cylinder is   
(a) 2 : 1
(b) 1 : 2
(c) 1 : 3
(d) 3 : 1

Question. Among the following, which one is/are correct ?     
(a) The slant height is the longest side of a pyramid.
(b) The section between the base and a plane parallel to the base of a solid is known as frustum.
(c) All the surfaces of a cuboid are square.
(d) For a cylinder, the top, the bottom and the walls of the cylinder determine the total surface area.

Question. If a sphere and a cube have equal surface areas, then the ratio of the diameter of the sphere to the edge of the cube is   
(a) 1 : 2
(b) 2 : 1
(c) í: 6
(d) √6 : √≠

Question. If the ratio of volumes of two cubes is 27 : 64, then the ratio of their surface area is:     
(a) 3 : 4
(b) 4 : 3
(c) 9 : 16
(d) 16 : 9

Question. If four times the sum of the areas of two circular faces of a cylinder of height 8 cm is equal to twice the curve surface area, then diameter of the cylinder is     
(a) 4 cm
(b) 8 cm
(c) 2 cm
(d) 6 cm

Question. A rectangular sheet of paper 40 cm × 22 cm, is rolled to form a hollow cylinder of height 40 cm. The radius of the cylinder (in cm) is     
(a) 3.5
(b) 7
(c) 80/7
(d) 5

Question. A Circular Cylinder can not be separated into     
(a) circular end at the bottom
(b) curved surface
(c) circular end at the top
(d) None of these

Question. A right circular cylinder has its height equal to two times its radius. It is inscribed in a right circular cone having its diameter equal to 10 cm and height 12 cm, and the axes of both the cylinder and the cone coincide. Then, the volume (in cm³) of the cylinder is approximately     
(a) 107.5
(b) 118.6
(c) 127.5
(d) 128.7

Question. Which one of the following is / are incorrect ?     
(a) Total surface area of cylinder is 2πr² + 2πrh.
(b) Total surface area of a sphere is 4πr².
(c) Total surface area of cone is πr² + πrl.
(d) None of these

Question. In the adjoining figure, the bottom of the glass has a hemispherical raised portion. If the glass is filled with orange juice, the quantity of juice which a person will get is     

(a) 135 π cm³
(b) 117 π cm³
(c) 99 π cm³
(d) 36 π cm³

Question. The number of solid cones with integer radius and integer height each having its volume numerically equal to its total surface area is     
(a) 0
(b) 1
(c) 2
(d) infinite

Question. Ratio of volumes of two cylinders with equal height is       
(a) H : h
(b) R : r
(c) R² : r²
(d) None of these

Question. Ratio of lateral surface areas of two cylinders with equal height is       
(a) 1 : 2
(b) H : h
(c) R : r
(d) None of these

Question. Ratio of volumes of two cones with same radii is     
(a) h₁ : h₂
(b) s₁ : s₂
(c) r₁ : r₂
(d) None of these

Question. A solid metallic cylinder of height 10 cm and diameter 14 cm is melted to make two cones in the proportion of their volumes as 3 : 4, keeping the height 10 cm, what would be the percentage increase in the flat surface area?     
(a) 9
(b) 16
(c) 50
(d) 200

Question. Consider a cuboid all of whose edges are integers and whose base is a square. Suppose the sum of all its edges is numerically equal to the sum of the areas of all its six faces. Then, the sum of all its edges is     
(a) 12
(b) 18
(c) 24
(d) 36

Question. Which one of the following is/ are made up of combinations of two or more of the basic solids?     
(a) Buildings
(b) Funnel
(c) Monuments
(d) Test-tube

Question. Shyam wants to make a solid brick shape structure from 400 wooden cubes of unit volume each. If the sides of the solid brick have the ratio 1 : 2 : 3, then the maximum number of cubes, which can be used, will be _______.     
(a) 400
(b) 288
(c) 300
(d) 384

We hope you liked the above Surface Area and Volume MCQ Class 10 Mathematics. In case you have any questions please put them in the comments box below and our teachers will provide you a response.