Continuity and Differentiability MCQ Questions Class 12 Mathematics
Please refer to MCQ Questions for Class 12 Mathematics Chapter 5 Continuity and Differentiability with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 12 Mathematics. Students should refer to MCQ Questions for Class 12 Mathematics with Answers to score more marks in Grade 12 Mathematics exams. Students should read the chapter Continuity and Differentiability and then attempt the following objective questions.
MCQ Questions for Class 12 Mathematics Chapter 5 Continuity and Differentiability with answers
MCQ Questions for Class 12 Mathematics Chapter 5 provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question.
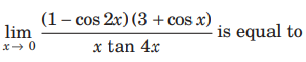
(a)−1/4
(b) 1/2
(c) 1
(2) 2
Answer
D
Question.
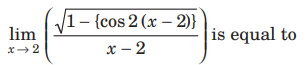
(a) √2
(b) − √2
(c) 1/√2
(d) does not exist
Answer
D
Question. The values of p and q for which the function B
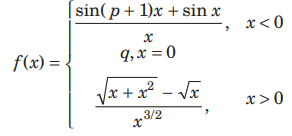
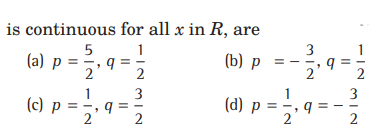
Answer
B
Question.

(a) 4
(b) − 4
(c) 0
(d) − 2
Answer
B
Question.

greatest integer function, then f is
(a) continuous for every real x
(b) discontinuous only at x = 0
(c) discontinuous only at non-zero integral values of x
(d) continuous only at x = 0
Answer
C
Question.
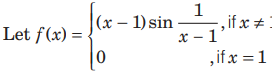
Then, which one of the following is true?
(a) f is differentiable at x = 1but not at x = 0.
(b) f is neither differentiable at x = 0 nor at x = 1.
(c) f is differentiable at x = 0 and x = 1.
(d) f is differentiable at x = 0 but not at x = 1.
Answer
D
Question.
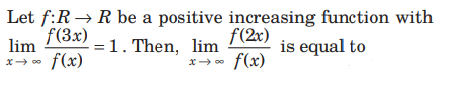
(a) 1
(b) 2/3
(c) 3/2
(d) 3
Answer
A
Question. The set of points, where f(x) = x/1+|x| is differentiable, is
(a) (-∞,-1)∪ (-1,∞)
(b) ( −∞, ∞)
(c) ( 0, ∞)
(d) ( -∞,0) ∪ (0,∞)
Answer
B
Question. Let f: R→ R : be function defined by f (x) = min
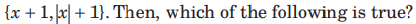
(a) f (x) ≥ 1for all x ∈ R
(b) f (x) is not differentiable at x = 1
(c) f (x) is differentiable everywhere
(d) f (x) is not differentiable
Answer
C
Question.
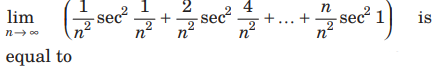
(a) 1/2 tan1
(b) tan1
(c) 1/2 cosec1
(d) 1/2 sec1
Answer
A
Question. If sin y = x sin (a + y), then dy/dx is equal to :
(a) sin √a / sin (a + y)
(b) sin2 (a + y)/sin a
(c) sin (a + y)
(d) None of these
Answer
B
Question. If y = 3 cos (log x) + 4 sin (log x), then
(a) xy2 + y1 + y = 0
(b) xy2 + y1 – y = 0
(c) x2y2 + xy1 + y = 0
(d) None of these
Answer
C
Question. If f(x) = 2x and g(x) = x2/2+1,then which of the following can be a discontinuous function?
(a) f(x) + g(x)
(b) f(x) – g(x)
(c) f(x).g(x)
(d) g(x)/f(x)
Answer
D
Question. If we can draw the graph of the function around a point without lifting the pen from the plane of the paper, then the function is said to be
(a) not continuous
(b) continuous
(c) not defined
(d) None of these
Answer
B
Question.
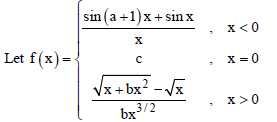
If f(x) is continuous at x = 0, then
(a) a + c = 0, b = 1
(b) a + c = 1, b ∈ R
(c) a + c = –1, b ∈ R
(d) a + c = –1, b = – 1
Answer
C
Question. Let f (x) = ex, g(x) = sin–1x and h (x) = f (g(x)), then h'(x)/h(x) =
(a) esin–1 x
(b) 1/ √1– x2
(c) sin–1 x
(d) 1/(1 – x2)
Answer
B
Question. If x = acos4θ, y = asin4θ, then dy/dx at θ = 3π/4 is
(a) – 1
(b) 1
(c) – a2
(d) a2
Answer
A
Question. If u = x2 + y2 and x = s + 3t, y = 2s – t, then d2u/ds2 is equal to
(a) 12
(b) 32
(c) 36
(d) 10
Answer
D
Question. If f (x) = x1/x – 1 for all positive x ≠ 1 and if f is continuous at 1, then x equals:
(a) 0
(b) 1/e
(c) e
(d) e2
Answer
A
Question. If f : R → R is defined by
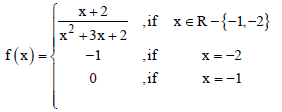
then f is continuous on the set
(a) R
(b) R – {– 2}
(c) R – {– 1}
(d) R – {– 1, – 2}
Answer
C
Question. At how many points between the interval (–∞, ∞) is the function f (x) = sin x is not differentiable.
(a) 0
(b) 7
(c) 9
(d) 3
Answer
A
Question. Let f : R → R be a function defined by
f (x) = min {x +1, |x| +1},Then which of the following is true ?
(a) f (x) is differentiable everywhere
(b) f (x) is not differentiable at x = 0
(c) f (x) ≥ 1 for all x ∈ R
(d) f (x) is not differentiable at x = 1
Answer
A
Question.
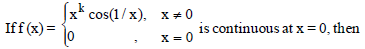
(a) k < 0
(b) k > 0
(c) k = 0
(d) k ≥ 0
Answer
B
Question. The value of λ, for which the function
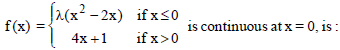
(a) 1
(b) – 1
(c) 0
(d) None of these
Answer
D
Question. If y = cot –1 (x2), then the value of dy/dx is equal to:
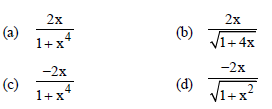
Answer
C
Question. If sec (x–y/x+y) = a, then dy/dx is
(a) –y/x
(b) x/y
(c) –x/y
(d) y/x
Answer
D
Question.
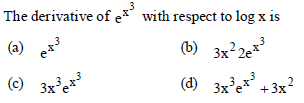
Answer
C
Question. If y = 2–x, then dy/dx is equal to :
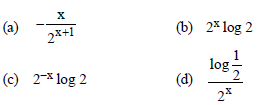
Answer
D
Question. If y = tan–1 (√x–x/1+x3/2), then y'(1) is equal to
(a) 0
(b) 1/2
(c) – 1
(d) – 1/4
Answer
D
Question.
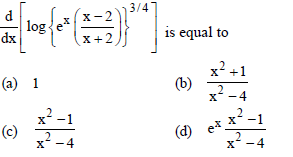
Answer
C
Question. If f(x) = x2 – sin x + 5, then
(a) f(x) is continuous at all points
(b) f(x) is discontinuous at x = π.
(c) It is discontinuous at x = π/2
(d) None of the above
Answer
A
Question.
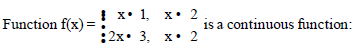
(a) for x = 2 only.
(b) for all real value of x such that x ≠ 2.
(c) for all real value of x.
(d) for all integral value of x only.
Answer
C
Question. Let f(x) = |sin x|. Then
(a) f is everywhere differentiable
(b) f is everywhere continuous but not differentiable at x = nπ, n ∈ Z
(c) f is everywhere continuous but not differentiable at x = (2n+1)π/2, n ∈ Z.
(d) None of these
Answer
B
Question.
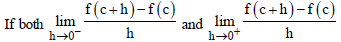
are finite and equal, then
(a) f is continuous at a point c
(b) f is not continuous at c
(c) f is differentiable at a point c in its domain
(d) None of the above
Answer
C
Question.
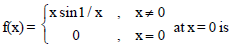
(a) continuous as well as differentiable
(b) continuous but not differentiable
(c) differentiable but not continuous
(d) neither continuous nor differentiable
Answer
B
Question. If f : R → R is defined by
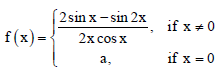
then the value of a, so that f is continuous at 0, is
(a) 2
(b) 1
(c) – 1
(d) 0
Answer
D
Question.
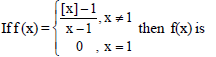
(a) continuous as well as differentiable at x = 1
(b) differentiable but not continuous at x = 1
(c) continuous but not differentiable at x = 1
(d) neither continuous nor differentiable at x = 1
Answer
D
Question. If y = e(1+log e x) , then dy/dx is equal to :
(a) e
(b) 1
(c) 0
(d) loge x . x
Answer
A
Question. If y = log (log x), then the value of ey dy/dx is :
(a) ey
(b) 1/x
(c) 1/(log x)
(d) 1/(x log x)
Answer
B
Question.
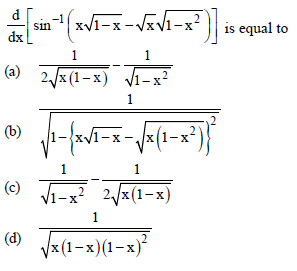
Answer
C
Question. The value of c in Rolle’s Theorem for the function f(x) = ex sinx, x ∈ [0, π] is
(a) π/6
(b) π/4
(c) π/2
(d) 3π/4
Answer
D
Question. If y = e1/2log(1+tan2x), then dy/dx is equal to
(a) 1/2sec2x
(b) sec2x
(c) sec x tan x
(d) e1/2log(1+tan2x)
Answer
C
Question.
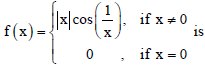
(a) discontinuous at x = 0
(b) continuous at x = 0
(c) Does not exist
(d) None of the above
Answer
B
Question. The derivative of
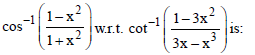
(a) 3/2
(b) 1
(c) 1/2
(d) 2/3
Answer
D
Question. Let y = t10 + 1 and x = t8 + 1, then d2y/dx2 is equal to
(a) 5/2 t
(b) 20t8
(c) 5/16t6
(d) None of these
Answer
C
Question.
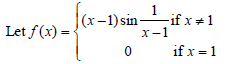
Then which one of the following is true?
(a) f is neither differentiable at x = 0 nor at x =1
(b) f is differentiable at x = 0 and at x =1
(c) f is differentiable at x = 0 but not at x = 1
(d) f is differentiable at x = 1 but not at x = 0
Answer
C
Question. Rolle’s Theorem holds for the function x3 + bx2 + cx, 1 ≤ x ≤ 2 at the point 4/3 , the value of b and c are
(a) b = 8, c = – 5
(b) b = – 5, c = 8
(c) b = 5, c = – 8
(d) b = – 5, c = – 8
Answer
B
STATEMENT TYPE QUESTIONS
Question. Suppose f and g be two real functions continuous at a real number c. Then, which of the following statements is/are true?
I. f + g is continuous at x = c.
II. f – g is continuous at x = c.
III. f . g is discontinuous at x = c.
IV. (f/g) is continuous at x = c (provided g(c) = 0)
(a) II and III are true
(b) III and IV are true
(c) I and II are true
(d) All are true
Answer
C
Question. Which of the following statements is/are true?
Statement I : The function f(x) = |cos x| is continuous function.
Statement II : The function f(x) = sin |x| is continuous function.
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Neither I nor II is true
Answer
C
Question. Which of the following functions is/are continuous?
I. Every rational function in its domain.
II. Sine function.
III. Cosine function.
IV. Tangent function is continuous in their domain.
(a) Only I is continuous
(b) Only II is continuous
(c) I and II are continuous
(d) All are continuous
Answer
D
Question. Which of the following is/are true?
Statement I: If x = a (θ – sin θ), y = a(1 + cos θ), then dy/dx = – cotθ/2.
Statement II : If x = sin3t/√cos 2t, y=cos3t/√cos 2t, then derivative of y with respect to x is – cot 3t.
(a) Only I is true.
(b) Only II is true.
(c) Both I and II are true.
(d) Neither I nor II is true.
Answer
C
Question.
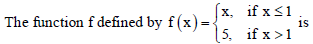
I. continuous at x = 0.
II. discontinuous at x = 1.
III. continuous at x = 2.
Then, which of the following is/are true?
(a) Only I is true
(b) Only II is true
(c) I and II are true
(d) All are true
Answer
D
Question. Consider the following statements:
I. The function f (x) = greatest integer ≤ x, x ∈ R is a continuous function.
II. All trigonometric functions are continuous on R.
Which of the statements given above is/are correct?
(a) Only I
(b) Only II
(c) Both I and II
(d) Neither I nor II
Answer
D
Question. Let f (x) be a differentiable even function. Consider the following statements:
(I) f ‘(x) is an even function.
(II) f ‘(x) is an odd function.
(III) f ‘(x) may be even or odd.
Which of the above statements is/are correct?
(a) Only I
(b) Only II
(c) I and III
(d) II and III
Answer
B
Assertion and Reason
Each of these questions contains two statements : Statement I (Assertion) and Statement II (Reason). Each of these questions also has four alternative choices, only one of which is the correct answer. You have to select one of the codes (a),(b ), (c ) ) and d given below.
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I.
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I.
(c) Statement I is true; Statement II is false.
(d) Statement I is false; Statement II is true.
Question. Statement I The function
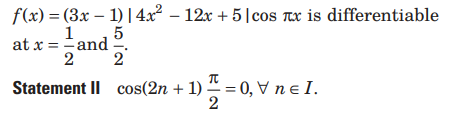
Answer
A

Answer
A
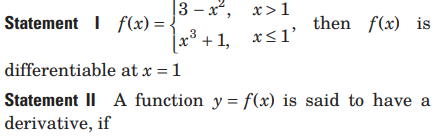
Answer
D
Question.
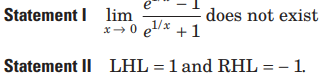
Answer
C
Question. Let f and g be real valued functions defined on interval (−1, 1) such that g′ ′(x) is continuous g(0)≠ g′(0)=0,g”(0)≠0 and f(x) = g(x) sin x.
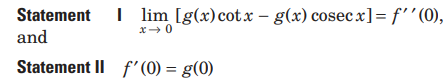
Answer
B
Question. Statement I The function f (x) = {x} , = where {⋅} denotes the fractional part function, is discontinuous at x = 1.
Statement II
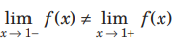
Answer
A
Question. Statement I f(x) = √x-2 + √(2-x) is continuous at x = 2 .
Statement II f(x) is a point function.
Answer
D
Question.
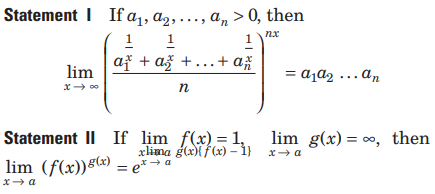
Answer
A
Question.

Answer
D
Question. Let f(x )= |x| = and g(x) =sin x
Statement I gof is differentiable at x = 0 and its derivative is continuous at that point.
Statement II gof is twice diffeerntiable at x = 0.
Answer
C
Question.
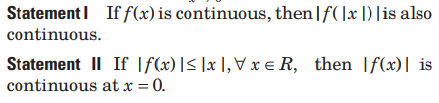
Answer
B
Question. Statement I f (x)= 1/{x} is discontinuous for integral values of x, where {} denotes the fractional part function.
Statement II For integral values of x, fx is not defined.
Answer
A
Question.
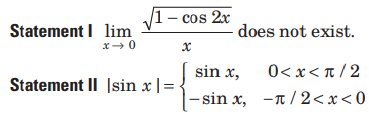
Answer
A
Question. Consider the function f(x)= (x)= |x-2 |+ |x-5 |,x ∈ R.
Statement I f ′ (4) = 0
Statement II f is continuous in [2,5] and differentiable in ( 2,5 ) and f(2)=f(5).
Answer
A
Question. Let f be a function satisfying
f (x) f (y)= f (x) + f (y) + f( xy)-2 for all x, y ∈ R , and f(2 )=5,, then
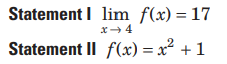
Answer
A
