Differential Equations MCQ Questions Class 12 Mathematics
Please refer to MCQ Questions for Class 12 Mathematics Chapter 9 Differential Equations with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 12 Mathematics. Students should refer to MCQ Questions for Class 12 Mathematics with Answers to score more marks in Grade 12 Mathematics exams. Students should read the chapter Differential Equations and then attempt the following objective questions.
MCQ Questions for Class 12 Mathematics Chapter 9 Differential Equations with answers
MCQ Questions for Class 12 Mathematics Chapter 9 provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. If xm yn = (x+y)m+n , then dy/dx is equal to
(a) x+y/xy
(b) xy
(c) x/y
(d) y/x
Answer
D
Question. The integrating factor of differential equation
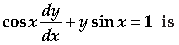
(A) cos x
(B) tan x
(C) sec x
(D) sin x
Answer
C
Question. Family y = Ax + A3 of curves is represented by the differential equation of degree:
(A) 1
(B) 2
(C) 3
(D) 4
Answer
A
Question. y = aemx + be−mx satisfies which of the following differential equation
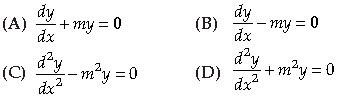
Answer
C
Question. The solution of


Answer
A
Question. Let g(x ) be the inverse of f (x ) such that f'(x) = 1/1+x5 , then d2(g(x))/dx2 is equal to
(a) 1/1+(g(x))5
(b) g'(x)/1+/(g(x))5
(c) 5(g(x))4 (1+(g(x))5
(d) 1+(g(x))5
Answer
C
Question. The general solution of dy/dx + y tan x = sec x is
(A) ysec x = tan x + C
(B) ytan x = sec x + C
(C) tan x = ytan x + C
(D) xsec x = tan y + C
Answer
A
Question. The general solution of differential equation (ex +1)ydy = (y+1)ex dx is
(A) (y + 1) = k (ex+ 1)
(B) y + 1 = ex + 1 + k
(C) y = log {k (y +1) (ex + 1)}
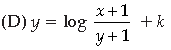
Answer
C
Question. The solution of differential equation
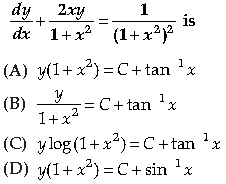
Answer
A
Question. d2x/dy2 is equal to

Answer
C
Question. If f(x) =|cos x – sin x | , then f’ (π/2) is equal to
(a) 1
(b) -1
(c) 0
(d) None of these
Answer
A
Question. If y = sec-1

(a) 0
(b) 1/√x+1
(c) 1
(d) None of these
Answer
A
Question. The solution of
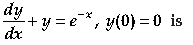
(A) y = e–x (x – 1)
(B) y = xex
(C) y = xe–x + 1
(D) y = xe–x
Answer
D
Question. Which of the following is a second-order differential equation?
(A) (y’)2 + x = y2
(B) y’ y” + y = sinx
(C) y”’ + (y”)2 + y = 0
(D) y’ = y2
Answer
B
Question. The integrating factor of differential equation
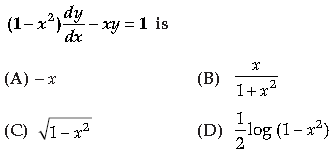
Answer
C
Question. The degree of differential equation
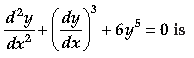
(A) 1
(B) 2
(C) 3
(D) 5
Answer
A
Question. The order of the differential equation
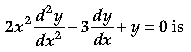
(A) 2
(B) 1
(C) 0
(D) not defined
Answer
A
Question. The numbers of arbitrary constants in the general solution of a differential equation of fourth order are:
(A) 0
(B) 2
(C) 3
(D) 4
Answer
D
Question. If y = tan-1

(a) 2
(b) 1
(c) 0
(d) -1
Answer
C
Question. If y = (x+√1+x2)n , then (1+x2) d2y/dx2 + x dy/dx is equal to
(a) n2y
(b) -n2y
(c) -y
(d) 2x2 y
Answer
A
Question. If √1-x2 + √1-y2 = a (x – y ), then dy/dx is equal to
(a) √1-x2/1-y2
(b) √1-y2/√1-x2
(c) √x2-1/1-y2
(d) √y2-1/1-x2
Answer
B
Question. If y = sin-1 (x√1-x + √x √1-x2) , then dy/dx is equal to
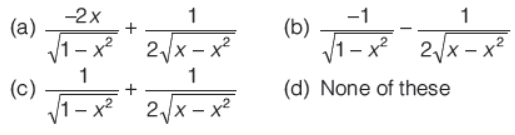
Answer
C
Question. If f(x) =

Question. The numbers of arbitrary constants in the particular solution of a differential equation of third order are:
(A) 3
(B) 2
(C) 1
(D) 0
Answer
D
Question. Which of the following differential equations has y = x as one of its particular solution?
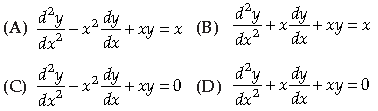
Answer
C
where P is a constant.Then, d2/dx2 { f (x )} at x = 0 is equal to
(a) P
(b) P + P 2
(c) P + P 3
(d) independent of P
Answer
D
Question. If f (x ) = (cos x + i sin x ) ×(cos 2x + i sin 2x ) (cos 3x + i sin 3x ) … (cos nx + i sinnx ) and f (1) =1, then f ” (1) is equal to

Answer
C
Question.
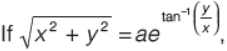
a>0 assuming y > 0, then y” (0) is equal to

Answer
C
Question. Let f ” (x ) = – f (x ), where f (x ) is a continuous double differentiable function and g(x ) = f ‘ (x ).

and F(5) = 5, then F (10) is equal to
(a) 0
(b) 5
(c) 10
(d) 25
Answer
B
Question. Let f(x) = elneg(x) and g(x+1) = x+g(x) ∀ x ∈ R. If n ∈ I +,
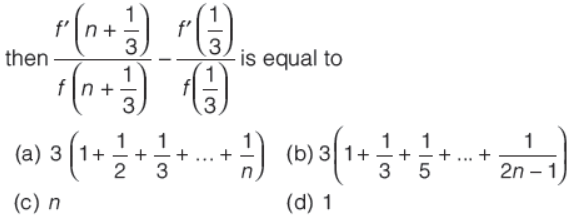
Answer
C
Question. For x ∈ R, f (x ) = | log2 – sin x | and g (x ) = f (f (x )), then
(a) g is not differentiable at x = 0
(b) g'(0) = cos(log2)
(c) g'(0) = – cos(log2)
(d) g is differentiable at x = 0 and g'(0) = – sin(log2)
Answer
B
Question. If f (2) = 4, f ‘ (2) = 3, f ” (2) =1, then (f ) -1 ” (4) is equal to
(a) -1/9
(b) -1/81
(c) -1/27
(d) -1/3
Answer
C
Question. If f (x ) = sin(sin x ) and f ” (x ) + tan x f ‘ (x ) + g(x ) = 0, then g(x ) is equal to
(a) cos2 x cos(sin x)
(b) sin2 cos(cos x)
(c) sin2 sin(cos x)
(d) cos2 sin(sin x)
Answer
D
Question. If x = a cost√cos2t and y = a sint√cos2t
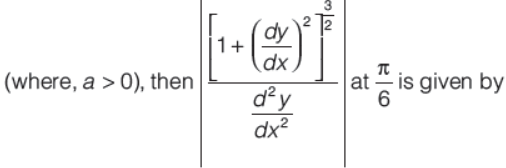
(a) a/3
(b) a √2
(c) √2/3a
(d) √2a/3
Answer
D
Question. If y = sin x × sin 2x × sin 3x… sinnx, then y’ is

Answer
B
Question. If f (x) = (x-1)100 (x-2)2(99) (x-3)3(98) …(x-100)100 , then the value of f'(101)/f(101) is
(a) 5050
(b) 2575
(c) 3030
(d) 1250
Answer
A
Question. If y = |sin x|x , then the value of dy/dx at x = -π/6 is

Answer
A
Question. The solution set of f ‘ (x ) > g’ (x ), where f(x) = 1/2 (5)2x+1 and g(x) = 5x + 4x loge 5 is
(a) (1,∞)
(b) (0, 1)
(c) (∞,0)
(d) (0, ∞)
Answer
D
Question. The derivative of the function represented parametrically as x = 2t – |t| , y = t3 + t2 |t| at t = 0 is
(a) -1
(b) 0
(c) 1
(d) does not exist.
Answer
B
Question. If 3f (x ) – 2f (1/x ) = x, then f ¢ (2) is equal to
(a) 2/7
(b) 1/2
(c) 2
(d) 7/2
Answer
B
Question.

(a) 1/5
(b) -1/5
(c) 6/7
(d) -6/7
Answer
A
Question. The degree of the differential equation
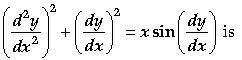
(A) 1
(B) 2
(C) 3
(D) not defined
Answer
D
Question. The order and degree of the differential equation
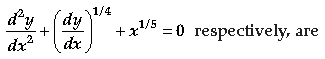
(A) 2 and 4
(B) 2 and 2
(C) 2 and 3
(D) 3 and 3
Answer
A
Question. If y = e–x (Acos x + Bsin x), then y is a solution of
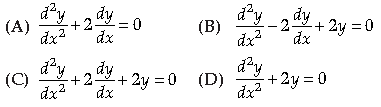
Answer
C
Question. The solution of differential equation xdy − ydx = 0 represents
(A) a rectangular hyperbola
(B) parabola whose vertex is at origin
(C) straight line passing through origin
(D) a circle whose centre is at origin
Answer
C
Question. The general solution of dy/dx = 2xex2−y is
(A) ex2 -y = C
(B) e-y + ex2 = C
(C) ey = ex2 + C
(D) ex2 + y = C
Answer
C
Question. The solution of equation (2y −1)dx − (2x +3)dy = 0 is
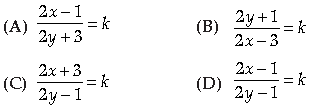
Answer
C
Question. The general solution of the differential equation
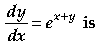
(A) ex + e-y = C
(B) ex + ey = C
(C) e-x + ey = C
(D) e-x + e-y = C
Answer
A
Question. The Integrating Factor of the differential equation

A) e–x
(B) e–y
(C) 1/x
(D) x
Answer
C
Case-based MCQs
Read the following text and answer the following questions on the basis of the same:
A Veterinary doctor as examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6°F. He took the temperature again after one hour; the temperature was lower than the first observation. It was 93.4°F. The room in which the cat was put is always at 70°F. The normal temperature of the cat is taken as 98.6°F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential
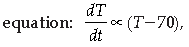
where 70°F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation
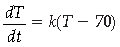
where k is a constant of proportion, time of death is calculated.
Question. What will be the degree of the above given differential equation?
(A) 2
(B) 1
(C) 0
(D) 3
Answer
B
Question. Which method of solving a differential equation helped in calculation of the time of death?
(A) Variable separable method
(B) Solving Homogeneous differential equation
(C) Solving Linear differential equation
(D) all of the above
Answer
A
Question. If the temperature was measured 2 hours after 11.30 pm, what will be the change in time of death?
(A) No change
(B) Death time increased
(C) Death time decreased
(D) Death time always constant
Answer
A
Question. The solution of the differential equation
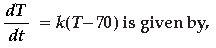
(A) log |T – 70| = kt + C
(B) log |T – 70| = log |kt|+ C
(C) T – 70 = kt + C
(D) T – 70 = kt C
Answer
A
Question. If t = 0 when T is 72, then the value of C is
(A) –2
(B) 0
(C) 2
(D) log 2
Answer
D
Read the following text and answer the following questions on the basis of the same:
Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 − y) where x denotes the number of weeks and y the number of children who have been given the drops.
Question. State the order of the above given differential equation.
(A) 2
(B) 1
(C) 0
(D) Can’t define
Answer
B
Question. Which method of solving a differential equation can be used to solve dy/dx = k(50 − y)?
(A) Variable separable method
(B) Solving Homogeneous differential equation
(C) Solving Linear differential equation
(D) all of the above
Answer
A
Question. The solution of the differential equation dy/dx = k(50 − y) is given by,
(A) log |50 – y| = kx + C
(B) –log |50 – y| = kx + C
(C) log |50 – y| = log|kx|+ C
(D) 50 – y = kx + C
Answer
B
Question. The value of C in the particular solution given that y(0) = 0 and k = 0.049 is
(A) log 50
(B) log (1/50/)
(C) 50
(D) –50
Answer
B
Question. Which of the following solutions may be used to find the number of children who have been given the polio drops?
(A) y = 50 – ekx
(B) y = 50 – e–kx
(C) y = 50(1 – e–kx)
(D) y = 50(e–kx – 1)
Answer
C
Read the following text and answer the following questions on the basis of the same:
The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours.

Question.
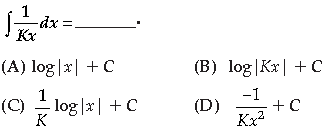
Answer
C
Question. If ‘N’ is the number of bacteria, the corresponding differential equation is _______.
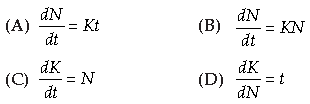
Answer
B
Question. The general solution is _______.
(A) log|N| = Kt + C
(B) log|Nt| = K + C
(C) log|N| = t
(D) log|Kt| = N + C
Answer
A
Question. If N0 is the initial count of bacteria, after 10 hours the count is _______.
(A) (1/5)log3
(B) 3log N0
(C) 9N0
(D) 2N0
Answer
C
Question. The bacteria becomes 10 times in _______ hours.

Answer
B
Read the following text and answer the following questions on the basis of the same:
A differential equation of the form dy/dx + Py = Q, where P and Q are functions of x alone, is called a first order linear differential equation. It has many applications in physics including RL circuits.
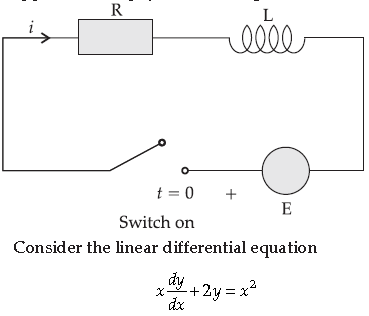
Question. ∫Qdx = _______.
(A) log |x| + C
(B) 2x + C
(C) log x2 + C
(D) x2/2 + C
Answer
D
Question. The value of ∫ Pdx = _______.
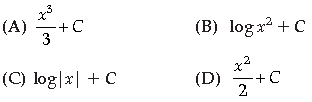
Answer
B
Question. The integrating factor is _______.
(A) log |x|
(B) 2x
(C) x2
(D) elog x
Answer
C
Question. The general solution is _______.
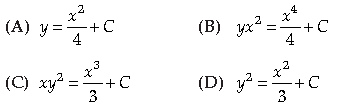
Answer
B
Question. If y(1) = 0, then y(2) = _______.
(A) 0
(B) 1
(C) 15/4
(D) 15/16
Answer
D
We hope you liked the above MCQ Questions for Class 12 Mathematics Chapter 9 Differential Equations . put them in the comments box below and our teache
