Relations and Functions MCQ Questions Class 12 Mathematics
Please refer to MCQ Questions for Class 12 Mathematics Chapter 1 Relations and Functions with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 12 Mathematics. Students should refer to MCQ Questions for Class 12 Mathematics with Answers to score more marks in Grade 12 Mathematics exams. Students should read the chapter Relations and Functions and then attempt the following objective questions.
MCQ Questions for Class 12 Mathematics Chapter 1 Relations and Functions with answers
MCQ Questions for Class 12 Mathematics Chapter 1 provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. The domain of the function f(x) = 1/√|x| – x is
(a) (0, ∞)
(b) (- ∞, 0)
(c) (- ∞, ∞) – (0)
(d) (- ∞, ∞)
Answer
B
Question: If f (x)f (1/x)= f(x)+ f(1/x),∀ x ∈ R-{0},where f (x) be a polynomial function and f(5) =126, then f(3) is equal to
(a) 28
(b) 26
(c) 27
(d) 25
Answer
A
Question: If fog x =|sinx | and gof =x = sin2√x then f(x) and g (x) are
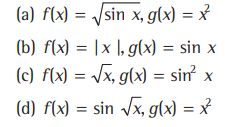
Answer
C
Question:
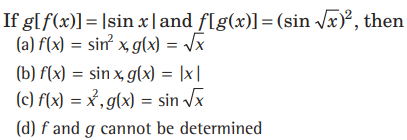
Answer
A
Question: If ‘f’ is a real valued function not identically zero, satisfying f(x+ y) + f(x-y) = 2f(x)⋅ f (y), ∀ x, y ∈ R , then f (x) is
(a) odd
(b) even
(c) neither even nor odd
(d) cannot say
Answer
B
Question:
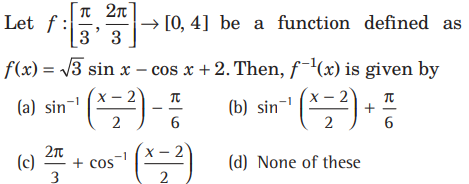
Answer
B
Question: If f is a function such that f(0)= 2, f(1)=3 and f (x+2) = 2f(x) -f(x+1) for every real x, then f( 5) is
(a) 7
(b) 13
(c) 1
(d) 5
Answer
B
Question: f (x) A
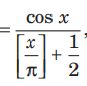
(where x is not an integral multiple of π and [x] denote the greatest integer function), is
(a) an odd function
(b) an even function
(c) neither odd nor even
(d) cannot be determined
Answer
A
Question: The period of the function f (x)=(sin(sin x/5) is
(a) 2π
(b) 2π /5
(c) 10π
(d) 5π
Answer
C
Question: If f (x) is a function that is odd and even simultaneously, then f(3) – f(2) is equal to
(a) 1
(b) –1
(c) 0
(d) 2
Answer
C
Question: sin ax + cos ax and |sinx | +|cosx | are periodic functions of same fundamental period, then a equals
(a) 0
(b) 1
(c) 2
(d) 4
Answer
D
Question: The function g(x)= a|sinx|xa2 | cos x| +f(a) has period equal to π/2, then a is equal to
(a) 2
(b) 3
(c) 1
(d) 4
Answer
C
Question: If f(x+2) +f(x)+1),then
(a)f(x+1)=f(x)
(b) f(x+1) =2f(x)
(c) f (x+2)=2f(x)
(d)f(x) is a periodic function
Answer
D
Question: Which of the following is a periodic function?
(a) x- [x[+ sinx
(b) sin[x ]
(c) x sin x
(d) (x-[x] cos (πx)
Answer
D
Question: The period of the function f (x)= |sinx |+|cosx| /sinx-cosx|
(a) π/4
(b) 2π
(c) π/2
(d) π
Answer
D
Question: The period of the function f(x )= |sinx|-|cosx| is equal to
(a) π/2
(b) π
(c) 2π
(d) 3π
Answer
B
Question: Let f( x)= tan-1x + cot-1x,g(x) = sin-1x + cos -1x, then
(a) f (x) and g (x) are periodic functions
(b) f (x) is periodic function but g (x) is not a periodic function
(c) f (x) and g(x) are non-periodic functions
(d) f[g (x)] is periodic function
Answer
B
Question: The void relation on a set A is
(a) reflexive
(b) symmetric and transitive
(c) reflexive and symmetric
(d) reflexive and transitive
Answer
B
Question: Let A ={0,1,2,3} and define a relation R on A as follows R={(0,0), (0,1) ,(0,3), (1,0), (1,1) ,(2,2), (3,0), (3,3), then R is
(a) reflexive
(b) symmetric
(c) transitive
(d) anti-symmetric
Answer
B
Question: A relation from P to Q is
(a) a universal set of P x Q
(b) P x Q
(c) an equivalent set of P x Q
(d) a subset of P x Q
Answer
D
Question: The relation R defined on the set A = { 1,2,3,4,5} by
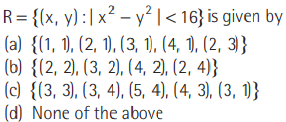
Answer
D
Question: For real numbers x and y, we write x Ry ⇔ x-y+√2 is an irrational number. Then, the relation R is
(a) reflexive
(b) symmetric
(c) transitive
(d) None of these
Answer
D
Question:

Answer
A
Question: Let R = {( a, a)}be a relation on a set A. Then, R is
(a) symmetric
(b) anti-symmetric
(c) symmetric and anti-symmetric
(d) neither symmetric nor anti-symmetric
Answer
C
Question:
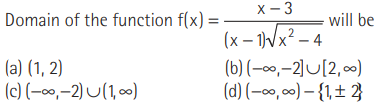
Answer
B
Question: Range of the function f (x)= x2+34x-71/x2+2x-7 is
(a) [5, 9]
(b) (-∞,5] ∪[9,∞)
(c) (5, 9)
(d) None of these
Answer
B
Question: Domain of the function f (x ) = √2- 2x2 is
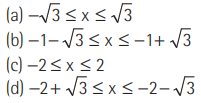
Answer
B
Question: The domain of the function =1/√|x|-x is
(a) (-∞,0)
(b) ( -∞,0]
(c) [ -,∞-1)
(d) (-∞ , ∞)
Answer
A
Question:
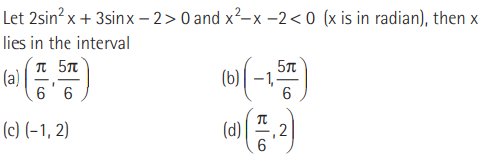
Answer
D
Question: The range of the function f (x) =1+x2/x2 is equal to
(a) [0, 1]
(b) (0, 1)
(c) (1,∞)
(d) (1,,∞)
Answer
C
Question:
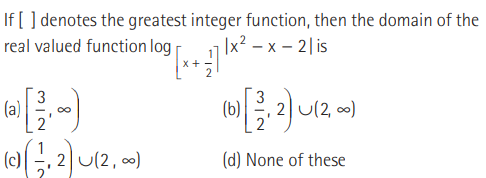
Answer
B
Question: If f : R→ R is given by f(x) = x2+3, then f-1(x) is equal to
(a) x1/3– 3
(b) x1/3 +3
(c) (x-3)1/3
(d) x+31/3
Answer
C
Question: If f : R → R be defined as f (x )+ sin x+ 7 then f (x ) is
(a) one one
(b) onto
(c) many one
(d) into
Answer
C
Question: The function f:R→ defined by f (x)= (x-1) (x-2) (x-3) is
(a) one one but not onto
(b) onto but not one one
(c) both one one and onto
(d) neither one one nor onto
Answer
B
Question:
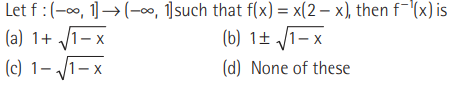
Answer
C
Question: If g (x)= x2+x-2 and 1/2 go f (x) = 2x2 -5x +2, then the value of f (x) is
(a) 2x-3
(b) 2x+3
(c) 2x2+3x+1
(d) 2x2-3x-1
Answer
A
Question: Let A be a set containing m distinct elements, then the total number of distinct functions from A to itself is
(a) mm
(b) m2
(c) m!
(d) 2m-1
Answer
A
Question: Which of the following functions are bijective?
(a) f :Z→ Z : defined by y= x+2
(b) f: Z→ Z → defined by y=2x
(c) f :R →R+ defined by y=√x =
(d) f: R→ R defined by y= x+|x|
Answer
A
Question: If f (x)= x3+ 3x2 + 12x- 2sin x, where f: R→ R, then
(a) f (x) is many one and onto
(b) f (x ) is one one and onto
(c) f (x) is one one and into
(d) f (x ) is many one and into
Answer
B
Question:
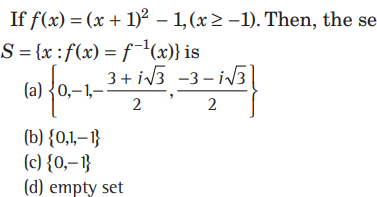
Answer
C
Question: The function f: R’ → (1,e) defined by f (x) =x2 +e/x2+1 is
(a) one one but not onto
(b) onto but not one one
(c) both one one and onto
(d) neither one one nor onto
Answer
C
Question. The number of real solutions of the equation log0.5 |x|= 2|x| is
(a) 1
(b) 2
(c) 0
(d) None of these
Answer
B
Question. If f :R → R is a function satisfying the property f(x +1) + f (x + 3) = 2 for all x ∈ R, then f is
(a) periodic with period 3
(b) periodic with period 4
(c) non- periodic
(d) periodic with period 5
Answer
B
Question. The period of the function f (x) = sin3 x + cos3 x is
(a) 2 π
(b) π
(c) 2π/3
(d) None of these
Answer
A
Question. For a real number x, [x ] denotes the integral part of x.
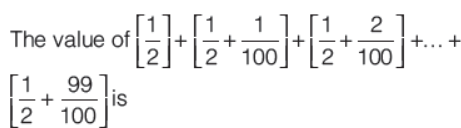
(a) 49
(b) 50
(c) 48
(d) 51
Answer
B
Question. Suppose f(x) = (x+1)2 for x ≥ -1 . If g(x) is the function, whose graph is reflection of the graph of f (x) w.r.t. the line y = x, then g(x) is equal to
(a) -√x-1 , x≥0
(b) 1/(x+1)2 , x > -1
(c) √x+1 , x ≥ – 1
(d) √x – 1 , x ≥ 0
Answer
D
Question. The function f : R →

(a) invertible
(b) injective but not surjective
(c) surjective but not injective
(d) neither injective nor surjective
Answer
C
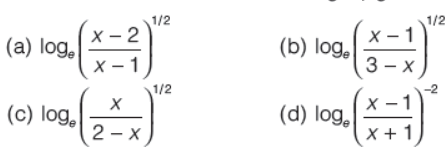
Question. The inverse of the function f(x) = ex – e-x/ex + e-x + 2 is given by
Answer
B
Question. If f (x ) is an invertible function, and g(x) = 2f (x) + 5, then the value of g-1 is
(a) 2f-1(x)-5
(b) 1/2f-1(x)+5
(c) 1/2 f-1(x)+5
(d) f-1(x-5/2)
Answer
D
Question. Let f : (2, 3) → (0,1) be defined by f (x ) = x – [x ] , then f-1 (x) is equal to
(a) x – 2
(b) x + 1
(c) x -1
(d) x + 2
Answer
D
Question. Let f :R → R be defined by f(x) = x2+1 . Then, pre-images of 17 and -3, respectively are
(a) f,{4,-4}
(b) {3,-3},φ
(c) {4,- 4},φ
(d) {4,-4},{2,-2}
Answer
C
Question. If [x]2 + x – a = 0 has a solution, where a ∈ N and a ≤ 20, then total number of different values of a can be
(a) 2
(b) 3
(c) 4
(d) 6
Answer
C
Question. If f2(x).f(1-x/1+x) = x3 , [where, x ≠ -1,1 and f (x ) ≠ 0], then find | [f (- 2)]| (where [.] is the greatest integer function)
(a) 1/ x
(b) 1 – x
(c) 1
(d) 2
Answer
D
Question. The period of the function f (x ) = [6x + 7] + cos πx – 6x, where [.] denotes the greatest integer function, is
(a) 3
(b) 2p
(c) 2
(d) None of these
Answer
C
Question. Statement I f (x ) = | x – 2| + | x – 3| + | x – 5| is an odd function for all values of x lie between 3 and 5.
Statement II For odd function f (-x ) = -f (x )
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I
(c) Statement I is true; Statement II is false
(d) Statement I is false; Statement II is true
Answer
B
Question. Let f (x ) = x10 + a. x8 + b. x6 + cx4 + dx2 be a polynomial function with real corfficient. If f (1) =1 and f (2) = -5, then the minimum number of distinct real zeroes of f (x) is
(a) 5
(b) 6
(c) 7
(d) 8
Answer
A
Question. If domain of f (x ) and g(x ) are D1 and D2 respectively, then domain of f (x) + g(x ) is D1 ∩ D2 then
Statement I The domain of the function f (x ) = sin-1 x + cos-1 x + tan-1 x is [-1,1].
Statement II sin-1x and cos -1x is defined in | x| ≤ 1and tan-1 x is defined for all x.
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I
(c) Statement I is true; Statement II is false
(d) Statement I is false; Statement II is true
Answer
A
Question. Total number of solutions of [x]2 = x + 2 {x} , where [×] and {} × denotes the greatest integer function and fractional part respectively, is equal to
(a) 2
(b) 4
(c) 6
(d) None of these
Answer
B
Question. Domain of f(x) = √x-1/x-2{x} , where {.} × denotes the fractional part of x, is
(a) (- ∞, 0) ∪ (0, 2]
(b) [1, 2)
(c) (- ∞, ∞) ~ [0, 2)
(d) (- ∞, 0) ∪ (0, 1] ∪ [2, ∞)
Answer
D
Question. Two sets A and B are defined as follows
A = {(x,y) : y = e2x , x ∈ R} and
B = {(x,y) : y = e2 , x ∈ R}, then
(a) A ⊂ B
(b) B ⊂ A
(c) A ∪ B
(d) A ∩ B = φ
Answer
D
Question. Range of f (x ) = [| sin x | + | cos x | ], where [×] denotes the greatest integer function, is
(a) {0}
(b) {0, 1}
(c) {1}
(d) None of these
Answer
C
Question. If the range of f (x ) is collection of all outputs f (x) corresponding to each real number in the domain, then Statement I The range of log(1/1+x2) is (- ∞, ∞).
Statement II When 0 < x ∈ 1, log x Î(- ∞, 0].
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I
(c) Statement I is true; Statement II is false
(d) Statement I is false; Statement II is true
Answer
D
Question. If f (x ) = sin x + cos x,g(x ) = x2 -1, then g { f (x )} is invertible in the domain
(a) [0,π/2]
(b) [-π/4 , π/4]
(c) [-π/2 , π/2]
(d) [0,π]
Answer
B
Question. Domain of definition of the function f (x) = √sin-1(2x) + π/6 for real valued x , is
(a) [-1/4 , 1/2]
(b) [-1/2 , 1/2]
(c) (-1/2 , 1/9)
(d) [-1/4 , 1/4]
Answer
A
Question. The function f (x ) = log(x +√x2+1) , is
(a) an even function
(b) an odd function
(c) a periodic function
(d) neither an even nor an odd function
Answer
B
Question. Domain of definition of the function f(x) = 3/4-x2 + log10(x3-x) , is
(a) (1, 2)
(b) (-1, 0) ∪ (1, 2)
(c) (1, 2) ∪ (2, ∞)
(d) (-1, 0) ∪ (1, 2) ∪ (2, ∞)
Answer
D
Question. Statement I The period of f(x) = 2cos 1/3 (x-π) + 4 sin 1/3(x-π) is 3π .
Statement II IfT is the period of f (x ), then the period of f (ax + b) is T/|a| .
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I
(c) Statement I is true; Statement II is false
(d) Statement I is false; Statement II is true
Answer
D
Question. If f (x ) and g(x ) are two functions such that f (x ) = [x ] + [-x ] and g(x ) = {x}∀ x ∈ R and h(x ) = f (g(x )) ; then which of the following is incorrect ?
([×] denotes greatest integer function and {.} denotes fractional part function).
(a) f (x) and h(x) are inertial functions
(b) f (x) = g(x) has no solution
(c) f (x) + h(x) > 0 has no solution
(b) f (x) – h(x) is a periodic function
Answer
B
Question. If f :R → R,f (x ) = x3 + , 3 and g :R → R,g(x) = 2x +1, then f-1 og-1 (23) equals
(a) 2
(b) 3
(c) 4
(d) 5
Answer
A
Question. If g(x ) =1+ x -[x ] and f(x) =
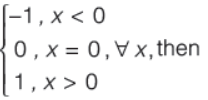
f {g(x )} is equal to
(a) x
(b) 1
(c) f (x)
(d) g(x)
Answer
B
We hope you liked the above MCQ Questions for Class 12 Mathematics Chapter 1 Relations and Functions. In case you have any questions please put them in the comments box below and our teache
