Vector Algebra MCQ Questions Class 12 Mathematics
Please refer to MCQ Questions for Class 12 Mathematics Chapter 10 Vector Algebra with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 12 Mathematics. Students should refer to MCQ Questions for Class 12 Mathematics with Answers to score more marks in Grade 12 Mathematics exams. Students should read the chapter Vector Algebra and then attempt the following objective questions.
Please refer to MCQ Questions for Class 12 Mathematics Chapter 10 Vector Algebra with answers below.
MCQ Questions for Class 12 Mathematics Chapter 10 Vector Algebra with answers
MCQ Questions for Class 12 Mathematics Chapter 10 provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. The value of k, for which the system of equations x + ky + 3z = 0, 3x + ky – 2z = 0 and2x + 3y – 4z = 0 possess a non-trivial solution over the set of rationals, is
(a) -33/2
(b) 33/2
(c) 11
(d) None of these
Answer
B
Question.
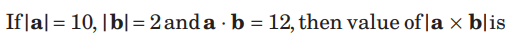
(a) 5
(b) 10
(c) 14
(d) 16
Answer
D
Question. The value of l for which the vectors
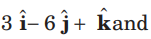
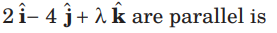
(a) 2/3
(b) 3/2
(c) 5/2
(d) 2/5
Answer
A
Question. The number of vectors of unit length perpendicular to the vectors
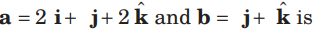
(a) one
(b) two
(c) three
(d) infinite
Answer
B
Question. For any vector a, the value of
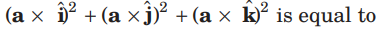
(a) a2
(b) 3a2
(c) 4a2
(d) 2a2
Answer
C
Question. The value of [a-b b-c c-a]is equal to
(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
Question.
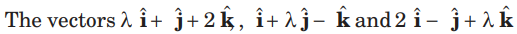
are coplanar , if
(a) λ = – 2
(b) λ = 0
(c) λ = 1
(d) λ= -1
Answer
A
Question. If a and b are two non-collinear vectors and xa +yb = 0
(a) x = 0 but y is not necessarily zero
(b) y = 0 but x is not necessarily zero
(c) x= 0, y=0
(d) None of the above
Answer
C
Question. Let ABCD be the parallelogram whose sides AB and AD are represented by the vectors
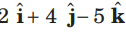
and
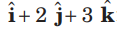
respectively. Then, if a is a unit vector parallel to AC, then a equal to
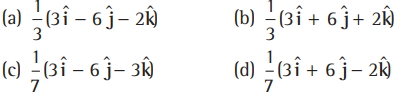
Answer
D
Question. If D, E and F are respectively the mid-points of AB, AC, and BC in Δ ABC, then BE +AF is equal to
(a) DC
(b) 1/2BF
(c) 2BF
(d) 3/2 BF
Answer
A
Question. If three points A, B and C have position vectors(1,x, 3), (3,4,7) and (y,-2,-5) respectively and if they are collinear, then (x ,y ) is equal to
(a) (2, 3)
(b) (-2, 3)
(c) (2, 3)
(d) (-2,-3)
Answer
A
Question. The value of a ·(b+ c) x)a+ b +c) is equal to
(a) 0
(b) a
(c) b
(d) c
Answer
A
Question. The points a -2b+ 3c, 2a+ 3b- 4c,- 7b+ 10c are
(a) collinear
(b) non-collinear
(c) can’t say
(d) None of these
Answer
A
Question. The area of the parallelogram whose adjacent sides are determined by the vectors
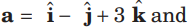
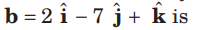
is
(a) 15 √2 sq units
(b) 3 √2 sq units
(c) 1/7 √2 sq units
(d) None of these
Answer
A
Question.
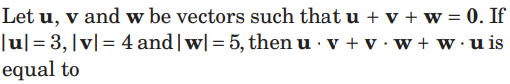
(a) 0
(b) 25
(c) -25
(d) 1
Answer
C
Question. For any three vectors a b c , and the value of [a+b b +c c+ a] equal to
(a) [abc]
(b)2[abc]
(c) 3[abc]
(d) None of these
Answer
B
Question. If ABCDEF is regular hexagon, then AB +EB+ FC is equal to
(a) 0
(b) 2AB
(c) 3AB
(d) 4AB
Answer
D
Question. Let a and b be two unit vectors such that angle between them is 60°. Then, |a-b| is equal to
(a) √5
(b) √3
(c) 0
(d) 1
Answer
D
Question. If position vector of a point A is a+ 2b and any point P(a) divides AB in the ratio of 2: 3, then position vector of B is
(a) 2a -b
(b) b- 2a
(c) a- 3b
(d) b
Answer
C
Question. Five points given by A, B, C, D and E are in a plane.
Three forces AC, AD and AE act at A and three forces CB, DB, EB act at B. Then, their resultant is
(a) 2AC
(b) 3AB
(c) 3DB
(d) 2BC
Answer
B
Question. a, b and c are mutually perpendicular unit vectors, then |a +b + c| is equal to
(a) √3
(b) 3
(c) 1
(d) 0
Answer
A
Question. The angle between a and b is 5π/6 and the projection of a in the direction of b is -6/√3,then| |a is equal to
(a) 6
(b) √3/2
(c) 12
(d) 4
Answer
D
Question.
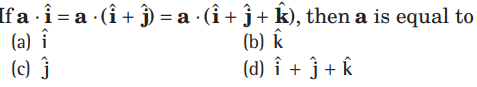
Answer
A
Question.
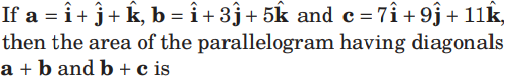
(a) 4√6
(b) 1/2√21
(c) √6/2
(d) √6
Answer
A
Question. If A, B, C, D and E are five coplanar points, then DA+ DB+ DC+ AE + BE CE equal to
(a) OE
(b) 3DE
(c) 2DE
(d) 4ED
Answer
B
Question.
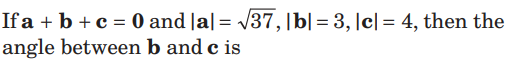
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer
C
Question.
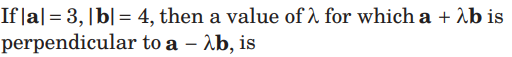
(a) 9/16
(b) 3/4
(c) 3/2
(d) 4/3
Answer
B
Question.
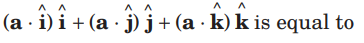
(a) a
(b) 2a
(c) 3a
(d) 0
Answer
A
Question. If the angle between
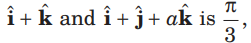
then the value of a is
(a) 0 or 2
(b) – 4 or 0
(c) 0 or -2
(d) 2 or -2
Answer
B
Question. Forces acting on a particle have magnitude 5, 3 and 1 unit and act in the direction of the vectors

respectively. They remain constant while the particle is displaced from the points A(2,-1,-3) to B(5,-1,1) The work done is
(a) 11 units
(b) 33 units
(c) 10 units
(d) 30 units
Answer
B
Question. A unit vector in xy-plane that makes an angle 45° with the vector
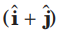
and an angle of 60° with the vector
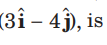

Answer
D
Question.
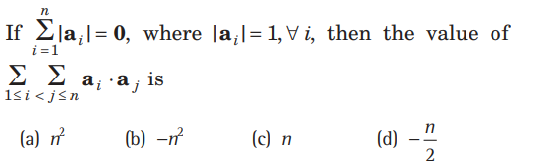
Answer
D
Question. The moment about the point M(-2,4,-6) of the force represented in magnitude and position AB, where the points A and B have the coordinates (1,2,-3) and (3,-4,2) respectively,

Answer
A
Question.
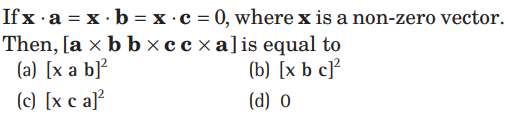
Answer
D
Question.
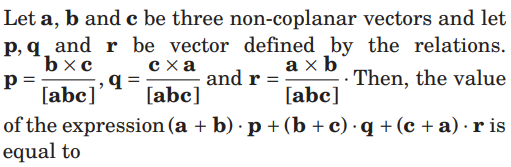
(a) 0
(b) 1
(c) 2
(d) 3
Answer
D
Question.
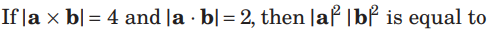
(a) 2
(b) 6
(c) 8
(d) 20
Answer
D
Question.
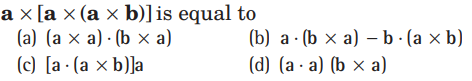
Answer
D
Question.

Question. The length of longer diagonal of the parallelogram constructed on 5a +2b and a- 3b. If it is given that |a| = 2 √2,|b| 3 and angle between a and b is p/4, is
(a) 15
(b) √113
(c) √593
(d) √369 C
Answer
D
Question. Between two numbers whose sum is 2,1/6 an even number of arithmetic means are inserted. If the sum of these means exceeds their number by unity, then the number of means are
(a) 12
(b) 10
(c) 8
(d) None of these
Answer
A
Question. If the sum of the first three terms of a GP is 21 and the sum of the next three terms is 168, then the first term and the common ratio is
(a) 3, 4
(b) 2, 4
(c) 3, 2
(d) None of these
Answer
C
Question. If the roots of the equation (a2+b2)x2 + 2(bc+ad)x + (c2+d2) = 0 are real, then a2 bd c2 , and are in
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
B
Question. If1 , ω and ω2 be the three cube roots of unity, then (1+ω)(1+ω2)(1+ω4)K n factors is equal to
(a) 1
(b) -1
(c) 0
(d) None of these
Answer
A
Question. If a < 0, then the positive root of the equation x2 – 2a |x-a| – 3a2 = 0 is
(a) a (- 1 – √6)
(b) a (1 – √2)
(c) a (1 – √6)
(d) a (1 + √2)
Answer
B
Question. Sum of n terms of series 12 + 16 + 24 + 40 + … will be
(a) 2(2n – 1) + 8n
(b) 2(2n – 1) + 6n
(c) 3(2n – 1) + 8n
(d) 4(2n – 1) + 8n
Answer
D
Question. 150 workers were engaged to finish a piece of work in a certain number of days. Four workers dropped the second day, four more workers dropped the third day and so on. It takes 8 more days to finish the work now.
Then, the number of days in which the work was completed is
(a) 29 days
(b) 24 days
(c) 25 days
(d) 26 days
Answer
C
Question. For all natural number n >1, 24n – 15n – 1 is divisible by
(a) 225
(b) 125
(c) 325
(d) None of these
Answer
A
Question. If b > a , then the equation (x – a)(x – b) -1 = 0, has
(a) both the roots in [a, b]
(b) both the roots in (-∞, a]
(c) both the roots in (b, ∞)
(d) one root in (-∞, a) and other in (b, ∞)
Answer
D
Question. The value of x satisfying log2(3x – 2) = log1/2 x is
(a) -1/3
(b) 2
(c) 1/2
(d) None of these
Answer
D
Question. If f(x,n) =
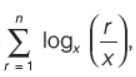
then the value of x satisfying the equation f (x,11) = f (x,12) is
(a) 10
(b) 11
(c) 12
(d) None of these
Answer
C
Question. The number of groups that can be made from 5 different green balls, 4 different blue balls and 3 different red balls, if atleast 1 green and 1 blue ball is to be included is
(a) 3700
(b) 3720
(c) 4340
(d) None of these
Answer
B
Question. If X is the set of all complex numbers z such that | z | =1, then the relation R defined on X by | arg z1 – arg z2 | = 2π/3 , is
(a) reflexive
(b) symmetric
(c) transitive
(d) anti-symmetric
Answer
B
Question. If a and b are the roots of the equation ax2 – 2bx + c = 0 , then α3β3 + α2β3 is equal to
(a) c2/a3 (c-2b)
(b) c2/a3 (c+2b)
(c) bc2/a3
(d) None of these
Answer
B
Question. If f(x) =
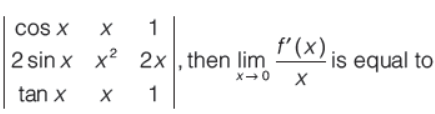
(a) 1
(b) -1
(c) 2
(d) – 2
Answer
D
Question. The maximum sum of the series 20+(19)1/3 + (18)2/3 + 18 + ……is
(a) 310
(b) 290
(c) 320
(d) None of these
Answer
A
Question. If A =
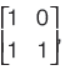
then which of the following is not true?
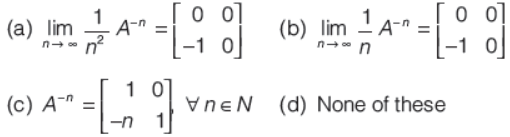
Answer
A
Question. The number of common terms to the two sequences 17, 21, 25, …, 417 and16, 21, 26, …, 466 is
(a) 21
(b) 19
(c) 20
(d) 91
Answer
C
Question. Let z1 , z2 , and z3 be three points on | z | =1. If θ1 , θ2 , and θ3 are the arguments of z1 ,z2 and z3 respectively, then cos(θ1 – θ2) + cos (θ2 – θ3) + cos (θ3 – θ1)
(a) ≥ 3/2
(b) ≥ – 3/2
(c) ≤ -3/2
(d) None of these
Answer
B
Question. There are 16 points in a plane no three of which are in a straight line except 8 which are all in a straight line. The number of triangles can be formed by joining them equals
(a) 1120
(b) 560
(c) 552
(d) 504
Answer
D
Question. Assume X,Y, Z,W and P are matrices of order 2 x n, 3 x k, 2 x p,n x 3 and p x k, respectively.
Now, consider the following statements
I. PY +WY will be defined for k = 3 and p = n.
II. The order of the matrix 7X – 5Z is n ´ 2 (if p = n).
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Neither I nor II is true
Answer
A
Question. The sum to n terms of the series
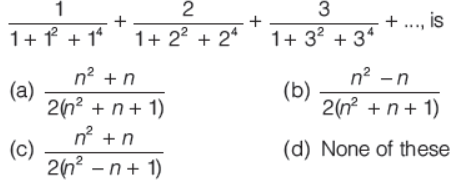
Answer
A
Question. Let a,b and c ∈ R and a ≠ 0. If a is a root of a2x2 + bx + c = 0, β is a root of a2x2 – bx – c = 0 and 0 < α < β, then the equation of a2x2 + 2bx + 2c = 0 has a root γ, that always satisfies
(a) γ = α
(b) γ = β
(c) γ = (α + β) / 2
(d) α < γ < β
Answer
D
Question. The three numbers a , b and c between 2 and 18 are such that their sum is 25, the numbers 2,a and b are consecutive terms of an AP and the numbers b,c and 18 are consecutive terms of a GP. The three numbers are
(a) 3, 8, 14
(b) 2, 9, 14
(c) 5, 8, 12
(d) None of these
Answer
C
Question. Which of the following is correct?
(a) Skew-symmetric matrix of an even order is always singular
(b) Skew-symmetric matrix of an odd order is non-singular
(c) Skew-symmetric matrix of an odd order is singular
(d) None of the above
Answer
C
Question. If
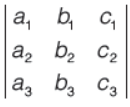
= 5, then the value of
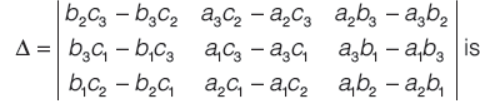
(a) 5
(b) 25
(c) 125
(d) 0
Answer
B
Question. A is a set containing n elements. A subset P of A is chosen. The set A is reconstructed by replacing the elements of P. A subset Q of A is again chosen. The number of ways of choosing P andQ, so that P Ç Q contains exactly two elements is
(a) 9.nC2
(b) 3n – nC2
(c) 2. nCn
(d) None of these
Answer
D
Question. The inequality | z – 4| < | z – 2| represents the region given by
(a) Re(z) > 0
(b) Re(z) < 0
(c) Re(z) > 3
(d) None of these
Answer
C
We hope you liked the above MCQ Questions for Class 12 Mathematics Chapter 10 Vector Algebra. In case you have any questions please put them in the comments box below and our teache
