Application of Derivatives MCQ Questions Class 12 Mathematics
Please refer to MCQ Questions for Class 12 Mathematics Chapter 6 Application of Derivatives with answers below. These multiple-choice questions have been prepared based on the latest NCERT book for Class 12 Mathematics. Students should refer to MCQ Questions for Class 12 Mathematics with Answers to score more marks in Grade 12 Mathematics exams. Students should read the chapter Application of Derivatives and then attempt the following objective questions.
MCQ Questions for Class 12 Mathematics Chapter 6 Application of Derivatives with answers
MCQ Questions for Class 12 Mathematics Chapter 6 provided below covers all important topics given in this chapter. These MCQs will help you to properly prepare for exams.
Question. A spherical balloon is be in gin flated at the rate of 35 cc/min. The rate of in crease in the sur face area (in cm2/min) of the balloon when its diameter is 14 cm, is
(a) 10
(b) √10
(c) 100
(d) 10 √10
Answer
A
Question.
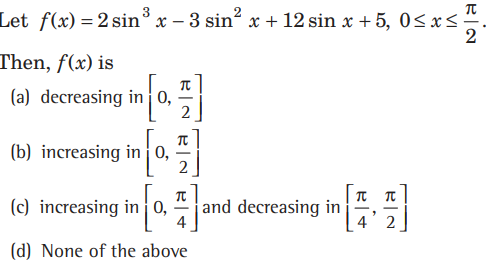
Answer
B
Question. If the line joining the points (0,3) and ( 5,-2) is a tangent to the curve y=c/x+1, then the value of c is
(a) 1
(b) –2
(c) 4
(d) None of these
Answer
C
Question. The angle of intersection of curves,
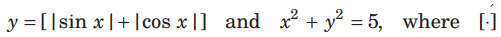
denotes greatest integral function is
(a) π/4
(b) tan−1 (1/2)
(c) tan −1 (2)
(d) None of these
Answer
C
Question. If m be the slope of a tangent to the curve ey=1+x2, then
(a) | m| > 1
(b) m <1
(c) | m| < 1
(d) | m| ≤ 1
Answer
D
Question. The area of the triangle formed by the coordinate axes and a tangent to the curve xy =a2 at the point ( x1,y1) on it is
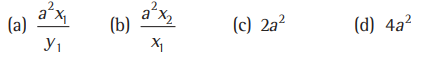
Answer
C
Question. If the line ax+ by+ c =0 is a normal to the curve
xy = 1, then
(a) a > 0, b > 0
(b) a > 0, b < 0
(c) a < 0, b > 0
(d) a < 0, b < 0
Answer
B
Question. The equation of tangent to the curve (x/a)n + (y/b)n=2 at (a,b) is
a) x/a+y/b=2
(b) x/a+y/b=1/2
(c) x/b-y/a=2
(d) ax+ by = 2
Answer
A
Question. The function f (x) =in(π+x)/in (e+x) is
(a) increasing on (0,∞)
(b) decreasing in (0, ∞)
(c) increasing on (0, π/e ), decreasing on (π/e,∞)
(d) decreasing on (0,π/e), increasing on (π /e,∞)
Answer
B
Question. Assuming the petrol burnt (per hour) in driving a motorboat varies as the cube of its velocity, then the most economical speed when going against a current of c miles per hour
(a) c/2 mph
(b) 2c/3 mph
(c) 3c/2 mph
(d) 2c mph
Answer
C
Question. If the curves y = ax and y = bx in ter sects at angle α , then tan α is equal to

Answer
B
Question. Function

is monotonic in creas ing, if
(a) λ > 1
(b) λ < 1
(c) λ < 4
(d) λ > 4
Answer
D
Question. The function f(x) = x/1+|x| is
(a) strictly increasing
(b) strictly decreasing
(c) neither increasing nor decreasing
(d) not differential at x = 0
Answer
A
Question. Oil is leaking at the rate of 16 cm3 /s from a vertically kept cylindrical drum containing oil. If the radius of the drum is 7 cm and its height is 60 cm. Then, the rate at which the level of the oil is changing when oil level is 18 cm, is
(a) -16/4π
(b) -16/48π
(c) 16/49π
(d) -16/47π
Answer
C
Question. The in ter val in which the func tion f (x) = x 1/x is
increasing, is
(a) (−∞, e)
(b) (e, ∞)
(c) (−∞, ∞)
(d) None of these
Answer
A
Question. If f (x ) = −2x3 + 21x2 – 60x + 41 , then
(a) f (x) is de creasi ng in (−∞, 1)
(b) f (x) is de creasi ng in (−∞, 2)
(c) f (x) is in creasi ng in (−∞, 1)
(d) f (x) is increasing in (−∞, 2)
Answer
B
Question. An an gle θ, 0 < θ < π/2 , which in creases twice as fast as its sine, is
(a) π/2
(b) 3π/2
(c) π/4
(d) π/3
Answer
D
Question. The value of x for which the polynomial 2x3 – 9x2 + 12x + 4 is a de creasing function of x, is
(a) −1< x < 1
(b) 0 < x < 2
(c) x > 3
(d) 1< x < 2
Answer
D
Question. If m is the slope of a tangent to the curve ey = 1 + x2 , then
(a) |m| ≤
(b) |m| > − 1
(c) |m| >1
(d) |m| >1
Answer
A
Question. The sum of inter cepts on co or di nate axes made by tan gent to the curve √x +√y = √a , is
(a) a
(b) 2a
(c) 2 √a
(d) None of these
Answer
A
Question. Line join ing the points (0, 3) and (5, −2) is a tan gent to the curve y = ax/1+x , then
(a) a = 1± √3
(b) a = φ
(c) a = −1± √3
(d) a = −2 ± 2 √3
Answer
B
Question. The tan gent at (1,7) to the curve x2 = y – 6 touches the circle x2 + y2 + 16x + 12y + c = 0 at
(a) (6, 7)
(b) (−6, 7)
(c) (6, − 7)
(d) (−6, − 7)
Answer
D
Question. The equa tion of the tan gent to the curve y = x + 4/x2 , that is par al lel to the X-axis, is
(a) y = 0
(b) y = 1
(c) y = 2
(d) y = 3
Answer
D
Question.

is increasing for all real values of x, then
(a) a ∈ (−1,1)
(b) a ∈ (1,5)
(c) a ∈ (1,∞)
(d) a ∈ (5,∞)
Answer
D
Question. f (x) sat is fies the conditions of Rolle’s the o rem in [1, 2] and f (x ) is con tin u ous in [1, 2], then ∫12 f'(x) dx is equal to
(a) 3
(b) 0
(c) 1
(d) 2
Answer
B
Question. The slope of the tan gent to the curve x = 3t2 + 1 , y = t3 – 1, at x =1 is
(a) 0
(b) 1/2
(c) ∞
(d) − 2
Answer
A
Question. Two men A and B start with ve loc i ties v at the same time from the junc tion of two roads in clined at 45° to each other. If they travel by dif fer ent roads, the rate at which they are be ing sep a rated.
(a) √2-√2 . v
(b) √2+√2 . v
(c) √2 – 1. v
(d) √2+√2 . v
Answer
A
Question. An gle be tween the tan gents to the curve y = x2 – 5x + 6 at the points (2, 0) and (3, 0) is
(a) π/2
(b) π/6
(c) π/4
(d) π/3
Answer
A
Question. The normal to the curve y(x − 2) (x − 3) = x + 6 at the point, where the curve intersects the Y-axis passes through the point
(a) (-1/2 , -1/2)
(b) (1/2 , 1/2)
(c) (1/2 , -1/3)
(d) (1/2 , 1/3)
Answer
B
Question. Coordinates of a point on the curve y = x logx at which the nor mal is par allel to the line 2 x − 2y = 3, are
(a) (0, 0)
(b) (e,e)
(c) (e2 , 2e2 )
(d) (e-2 , -2e-2)
Answer
D
Question. The length of the lon gest interval, in which the function x – 4 sin3 x is increasing, is
(a) π/3
(b) π/2
(c) 3π/2
(d) π
Answer
A
Question. Moving along the X-axis there are two points with x =10 + 6t, x = 3 + t2. The speed with which they are reaching from each other at the time of encounter is (x is in centimetre and t is in seconds)
(a) 16 cm/s
(b) 20 cm/s
(c) 8 cm/s
(d) 12 cm/s
Answer
C
Question. The position of a point in time ‘ t’ is given by x = a + bt −ct2 , y = at + bt2 . Its ac celeration at time ‘ t’ is
(a) b − c
(b) b + c
(c) 2b − 2c
(d) 2√b2+c2
Answer
D
Question. If the line ax + by + c = 0 is nor mal to curve xy + 5 = 0, then
(a) a + b = 0
(b) a > 0
(c) a < 0, b < 0
(d) a = − 2b
Answer
C
Question. If f and g are dif fer en tia ble func tions in (0,1) satis fying f (0) = 2 = g(1),g(0) = 0 and f (1) = 6, then for some c ∈] 0,1[
(a) 2f ‘ (c) = g’ (c)
(b) 2f ‘ (c) = 3g’ (c)
(c) f ‘ (c) = g’ (c)
(d) f ‘ (c) = 2g’ (c)
Answer
D
Question. The length of sub nor mal to the curve y = x/1-x2 at the point having abscissa √2 is
(a) 5 √2
(b) 3 √3
(c) √3
(d) 3 √2
Answer
D
Question. Let a + b = 4, a < 2 and g(x ) be a monotonically increasing function of x. Then,

(a) increases with increase in (b − a)
(b) decreases with increase in (b − a)
(c) increases with decreases in (b − a)
(d) None of the above
Answer
A
Question. An object is moving in the clock wise di rection around the unit circle x2+y2 = 1 As it passes through the point (1/2 , √3/2) , its y-coordinate is de creasing at the rate of 3 units per second. The rate at which the x-coordinate changes at this point is (in unit per second)
(a) 2
(b) 3 √3
(c) √3
(d) 2 √3
Answer
B
Question. If the curves x2/α + y2/4 = 1 and y3 = 16x intersect at right angles, then the value of α is
(a) 2
(b) 4/3
(c) 1/2
(d) 3/4
Answer
B
Question. In [0, 1], Lagrange’s mean value the o rem is not applicable to

Answer
A
Question. If f(x) = x/sin x and g(x) = x/tan x , where 0 < x ≤ 1, then in this interval
(a) both f (x) and g(x) are increasing functions
(b) both f (x) and g(x) are decreasing functions
(c) f (x) is an increasing function
(d) g(x) is an increasing function
Answer
C
Question. If the curves y2 = 6x , 9x2 + by2 = 16 intersect each other at right angles, then the value of b is
(a) 6
(b) 7/2
(c) 4
(d) 9/2
Answer
D
Question. If the volume of a sphere is in creas ing at a constant rate, then the rate at which its radius is increasing, is
(a) a constant
(b) proportional to the radius
(c) inversely proportional to the radius
(d) inversely proportional to the surface area
Answer
D
Question. The tangent drawn at the point (0, 1) on the curve y = e2x , meets X-axis at the point
(a) (1/2 , 0)
(b) (-1/2 , 0)
(c) (2, 0)
(d) (0, 0)
Answer
B
Question. A value of C for which the con clusion of mean value the o rem holds for the function f(x) = loge x on the interval [1, 3] is
(a) 2 log3 e
(b) 1/2 log3e
(c) log3e
(d) loge3
Answer
A
Question. If f(x) = 1/x+1 -log(1+x) , x > 0, then f is
(a) an increasing function
(b) a decreasing function
(c) both increasing and decreasing function
(d) None of the above
Answer
B
Question. A kite is moving horizon tally at a height of 151.5 m. If the speed of kite is 10 m/s, how fast is the string be ingletout, when the kite is 250 m away from the boy who is flying the kite? The height of boy is 1.5 m.
(a) 8 m/s
(b) 12 m/s
(c) 16 m/s
(d) 19 m/s
Answer
A
Question. The product of the lengths of subtangent and subnormal at any point of a curve is
(a) square of the abscissa
(b) square of the ordinate
(c) constant
(d) None of these
Answer
B
Question. The val ues of a for which the func tion (a + 2)x3 − 3ax2 + 9ax −1 = 0 decreases monotonically through out for all real x, are
(a) a < − 2
(b) a > − 2
(c) −3 < a < 0
(d) −∞ < a ≤ − 3
Answer
D
Question. If f'(sin x) < 0 and f” (sin x) > , 0 ∀ x ∈ (0,π/2) and g(x ) = f (sin x ) + f (cos x ), then g(x ) is de creas ing in
(a) (π/4 , π/2)
(b) (0,π/4)
(c) (0,π/2)
(d) (π/6 ,π/2)
Answer
B
Question. The an gle of in ter section of curves, y = [| sin x | + | cos x | ] and x2 + y2 = 5 , where [.] denotes great est integral function is
(a) π/4
(b) tan-1(1/2)
(c) tan-1(2)
(d) None of these
Answer
C
Question. If the function f(x) = x3 – 6x + ax + b satisfies Rolle’s the o rem in the interval [1, 3] and f’ (2√3+1/√3) = 0, then
(a) a = −11
(b) a = − 6
(c) a = 6
(d) a = 11
Answer
D
Question. If f (x ) = (x −p)(x −q)(x −r ), where p < q < r , are real numbers, then application of Rolle’s theorem on f leads to
(a) (p + q + r )(pq + qr + rp) = 3
(b) (p + q + r )2 = 3(pq + qr + rp)
(c) (p + q + r)2 >3(pq + qr + rp)
(d) (p + q + r )2<3(pq + qr + rp)
Answer
C
Question. If f (x ) is a monotonic poly nom ial of 2m −1 degree, where m ∈ N, then the equation [f (x ) + f (3x ) + f (5x ) +…+ f (2m −1)x ] = 2m −1 has
(a) atleast one real root
(b) 2m roots
(c) exactly one real root
(d) (2m + 1) roots
Answer
A
Question. A spherical balloon is filled with 4500 p cu m of he lium gas. If a leak in the balloon causes the gas to escape at the rate of 72p cu m/min, then the rate (in m/min) at which the radius of the balloon decreases 49 min after the leakage began is
(a) 9/7
(b) 7/9
(c) 2/9
(d) 9/2
Answer
C
Question. If f (x ) = sin x − cos x, the in terval in which function is decreasing in 0 ≤ x ≤ 2 p, is
(a) [5π/6 ,3π/4]
(b) [π/4 , π/2]
(c) [3π/2 , 5π/2]
(d) None of these
Answer
D
Question. The ab scissa of the points of the curve y = x3 in the in ter val [−2, 2], where the slope of the tangents can be obtained by mean value theorem for the in terval [−2, 2], are
(a) ±2/√3
(b) + √3
(c) ±√3/2
(d) 0
Answer
A
Question. If y = f (x ) is the equat ion of a par ab ola which is touched by the line y = x at the point where x =1, then
(a) 2f ‘ (0) = 3f ‘ (1)
(b) f ‘ (1) = 1
(c) f (0) + f ‘ (1) + f ” (1) = 2
(d) 2f (0) = 1 + f ‘(0)
Answer
B
Question. Water is dripping out from a conical funnel of semi-vertical angle π/4 at the uni form rate of 2 cm2 /s in the sur face area, through a tiny hole at the vertex of the bottom. When the slant height of cone is 4 cm, the rate of decrease of the slant height of water, is
(a) √2/4π cm/s
(b) 1/4π cm/s
(c) 1/π√2 cm/s
(d) None of these
Answer
A
Question. If the normal to the curve y2 = 5x – 1 at the point (1,−2) is of the form ax − 5y + b = 0, then a and b are
(a) 4,− 14
(b) 4,14
(c) −4,14
(d) 4,2
Answer
A
Question. If f (x ) satisfies the conditions for Rolle’s the or em in [3, 5], then ∫35 f(x) dx is equal to
(a) 2
(b) −1
(c) 0
(d) -4/3
Answer
D
Question. If f (x ) sat isfy all the con di tions of mean value the or em in [0, 2 ]. If f (0) = 0 and | f ‘ (x )| ≤ 1/2 for all x in [0, 2 ], then
(a) f (x) < 2
(b) |f (x)| ≤ 1
(c) f (x) = 2x
(d) f (x) = 3 for atleast one x in [0, 2]
Answer
B
Question. The curve y = ax3 + bx2 + cx + 5 touches the X-axis at P(−2, 0) and cuts the Y-axis at a point Q, where its gra di ent is 3. Then,
(a) a = -1/2 , b = -3/4 and c = 3
(b) a = 1/2 , b = -3/4 and c = − 3
(c) a = 1/2 , b = -1/4 and c = 3
(d) None of the above
Answer
A
Question. In the mean value the or em, f (b) − f (a) = (b − a)f’ (c), if a = 4,b = 9 and f (x ) = √x , then the value of c is
(a) 8.00
(b) 5.25
(c) 4.00
(d) 6.25
Answer
D
Question. The nor mal to the curve x2+2xy – 3y2 = 0 at (1,1)
(a) does not meet the curve again
(b) meets the curve again in the second quadrant
(c) meets the curve again in the third quadrant
(d) meets the curve again in the fourth quadrant
Answer
D
We hope you liked the above MCQ Questions for Class 12 Mathematics Chapter 6 Application of Derivatives. In case you have any questions please put them in the comments box below and our teache
